Testi on tarkoitettu kisallioppiminen.fi -sivustolla olevan Vektorit-kurssin ensimmäisen luvun itsearviointiin.
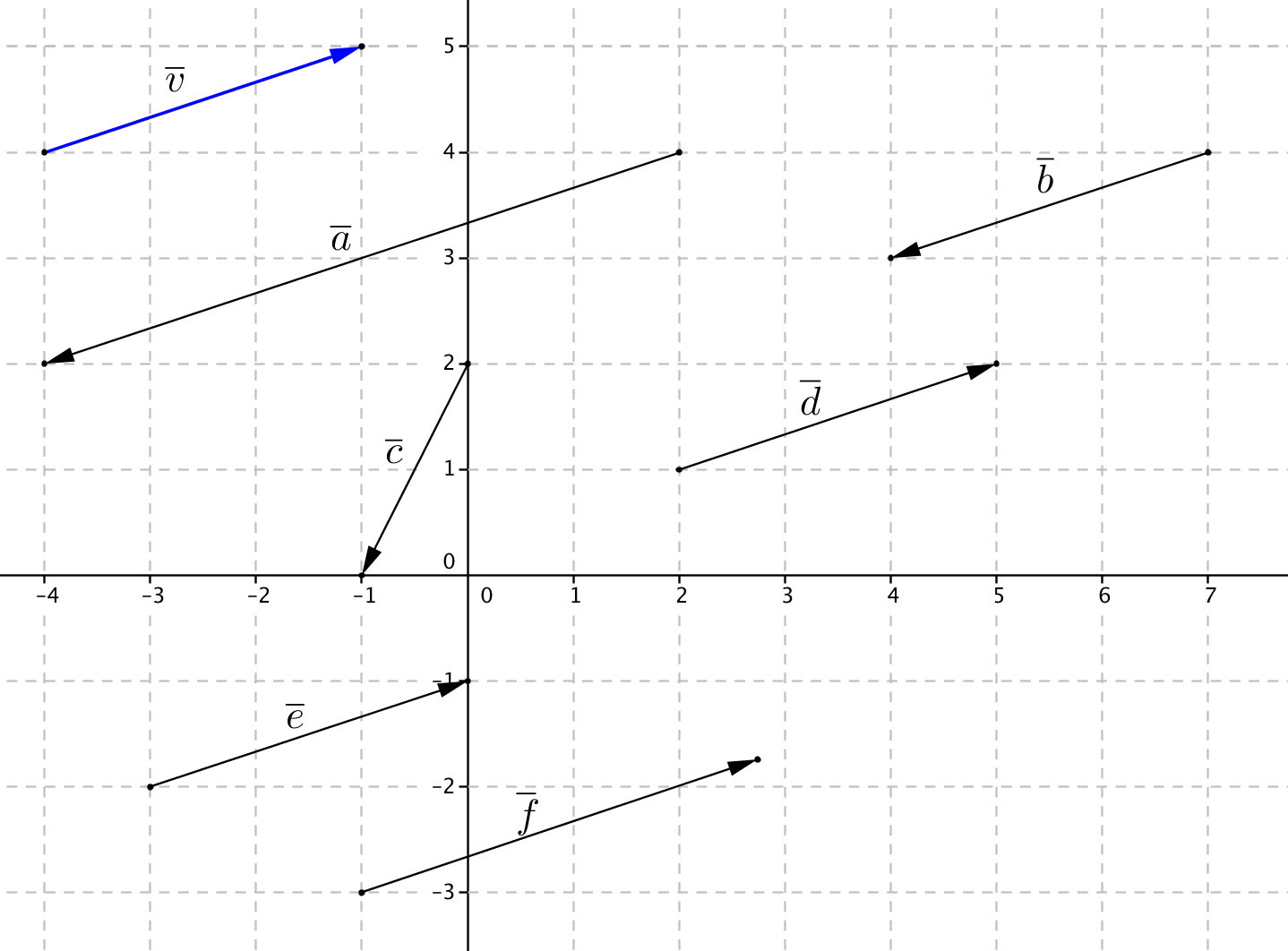
Tarkastele kuvaa. Mitkä kuvan vektoreista ovat
a) vektorin $\overline{v}$ kanssa samoja vektoreita
b) vektorin $\overline{v}$ kanssa samansuuntaisia
c) vektorin $\overline{v}$ kanssa vastakkaissuuntaisia
d) vektorin $\overline{v}$ kanssa yhdensuuntaisia
e) vektorin $\overline{v}$ vastavektoreita
f) vektorin $\overline{v}$ kanssa yhtä pitkiä?
a) Vektorit $\overline{d}$ ja $\overline{e}$. (1 p.)
Perustelu: Vektori ovat samat, jos ne voidaan esittää samalla tavalla vektoreiden $i$ ja $j$ avulla. Kuvassa se tarkoittaa, että vektorit ovat samansuuntaiset ja yhtä pitkät.
b) Vektorit $\overline{d}$, $\overline{e}$ ja $\overline{f}$. (1 p.)
Perustelu: Vektorit ovat samansuuntaiset, jos vektorit kulkevat yhtä jyrkästi ja nuolet ovat samaan suuntaan.
c) Vektorit $\overline{a}$ ja $\overline{b}$. (1 p.)
Perustelu: Vektorit ovat vastakkaissuuntaiset, jos vektorit kulkevat yhtä jyrkästi ja nuolet ovat vastakkaisiin suuntiin.
d) Vektorit $\overline{a}, \overline{b}, \overline{d}, \overline{e}$ ja $\overline{f}$. (1 p.)
Perustelu: Vektorit ovat yhdensuuntaisia, jos ne ovat saman- tai vastakkaissuuntaisia.
e) Vektori $\overline{b}$. (1 p.)
Perustelu: Vektorin vastavektori $-\overline{v}$ on vastakkaissuuntainen ja yhtä pitkä kuin vektori $\overline{v}$.
f) Kuvan perusteella vektorit $\overline{b}, \overline{d}$ ja $\overline{e}$. (1 p.)
Perustelu: Kuvasta voi laskea ruutuja vektoreiden $\overline{i}$ ja $\overline{j}$ suuntaan ja soveltaa Pythagoraan lausetta.
Tarkastele kuvaa.
a) Ilmoita kuvassa näkyvä vektori \(\overline{a}\) vektoreiden \(\overline{i}\) ja \(\overline{j}\) avulla.
b) Laske vektorin \(\overline{a}\) pituus.
c) Aseta vektori \(\overline{a}\) alkamaan origosta. Mikä on vektorin \(\overline{a}\) päätepiste?

a) \(\overline{a}=-4\overline{i}+3\overline{j}\) (2 p.)
Perustelu: Vektorissa \(\overline{a}\) kuljetaan neljä ruutua vasemmalle, eli vektorin \(\overline{i}\) kerroin on -4. Lisäksi pystysuunnassa kuljetaan 3 ruutua ylös, eli vektorin \(\overline{j}\) kerroin on 3. Voit antaa yhden pisteen per oikea kerroin.
b) Vektorin \(\overline{a}\) pituus on
\(|\overline{a}|=\sqrt{(-4)^2+3^2}=\sqrt{25}=5\). (2 p.)
Perustelu: Vektorin pituutta laskettaessa vektoreiden \(\overline{i}\) ja \(\overline{j}\) kertoimet korotetaan toiseen ja otetaan niiden summasta neliöjuuri.
c) Kuvasta nähdään, että vektorin \(\overline{a}\) päätepiste on \((-4,3).\) (2 p.)

Toinen tapa perustella pisteen koordinaatit on ajatella vektori \(\overline{a}\) paikkavektorina, jolloin vektorien \(\overline{i}\)ja \(\overline{j}\)kertoimet ovat suoraan vektorin päätepisteen \(x\)- ja \(y\)-koordinaatit.
Olkoon vektori $\overline{v}=3\overline{i}-2\overline{j}$.
Vektori $\overline{v}$ asetetaan alkamaan pisteestä $(1,-2)$. Määritä laskemalla vektorin $\overline{v}$ päätepiste. Piirrä kuva ratkaisun tueksi.
Piirretään ensin tilanteesta kuva. (Vektorit $\overline{OA}$ ja $\overline{OP}$ eivät tarvitse olla näkyvissä.) (1 p.)

Koska kysytään vektorin $\overline{v}$ päätepistettä, muodostetaan paikkavektori vektorin $\overline{v}$ päätepisteeseen $P$. Etsitään reitti origosta $O$ pisteeseen $P$ kuvan avulla. Saadaan
$\overline{OP}=\overline{OA}+\overline{AP}=\overline{OA}+\overline{v}$. (2 p.)
Koska $\overline{OC}=1\overline{i}-2\overline{j}=\overline{i}-2\overline{j}$ (1 p.), saadaan sijoittamalla tämä ja vektorin $\overline{v}$ lauseke
$\overline{OP}=(\overline{i}-2\overline{j})+(3\overline{i}-2\overline{j})=(1+3)\overline{i}+(-2-2)\overline{j}=4\overline{i}-4\overline{j}$. (1 p.)
Pisteen $P$ koordinaatit ovat siis $(4,-4)$, jonka kuva vahvistaa.
Vastaus: Vektorin $\overline{v}$ päätepiste on $(4,-4)$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
