Testi on tarkoitettu kisallioppiminen.fi -sivustolla olevan Vektorit-kurssin neljännen luvun itsearviointiin.
Kolmion $ABC$ sivuvektorit ovat $\overline{AB}=\overline{a}$ ja $\overline{AC}=\overline{b}$. Piste $P$ jakaa sivun $BC$ suhteessa $3:2$. Lausu vektori $\overline{BP}$ vektoreiden $\overline{a}$ ja $\overline{b}$ avulla.
Piirretään kuva. (1 p.)
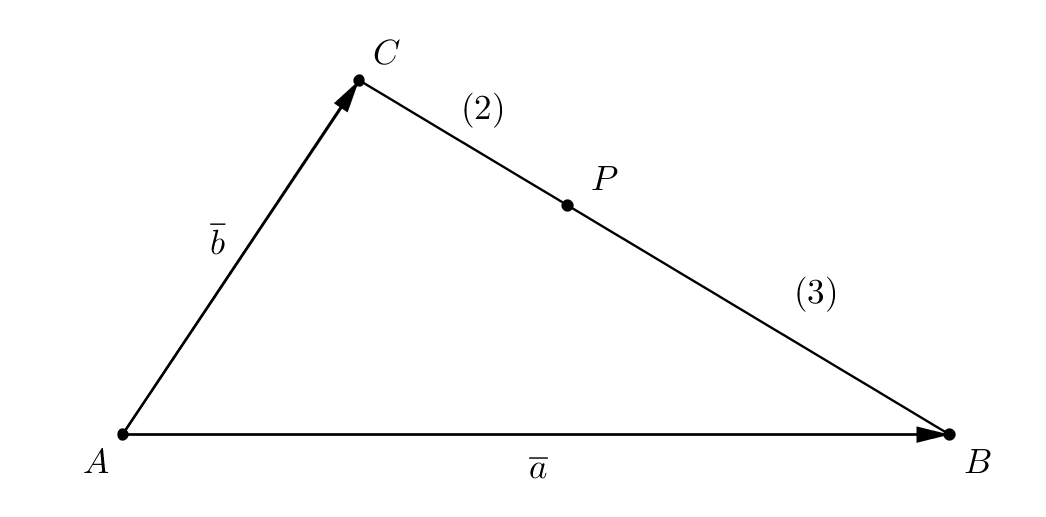
Etsitään reitti pisteestä $B$ pisteeseen $P$ niin, että reitissä esiintyy pelkkiä vektoreita $\overline{a}$ ja $\overline{b}$. Koska piste $P$ jakaa sivun $BC$ suhteessa $3:2$, on
$$\overline{BP}=\dfrac{3}{5}\overline{BC}. \text{ (1 p.)}$$
Nyt vektori $\overline{BP}$ on siis ilmoitettu vektorin $\overline{BC}$ avulla. Jatketaan vektorin $\overline{BC}$ ilmoittamista eri tavalla, eli etsitään reittiä pisteestä $B$ pisteeseen $C$. Saadaan
$$\overline{BP}=\dfrac{3}{5}\overline{BC}=\dfrac{3}{5}(\overline{BA}+\overline{AC}) \text{ (2 p.)},$$ josta saadaan
$$\overline{BP}=-\dfrac{3}{5}\overline{AB}+\dfrac{3}{5}\overline{AC}=-\dfrac{3}{5}\overline{a}+\dfrac{3}{5}\overline{b}. \text{ (2 p.)}$$
Vastaus: Vektori $\overline{BP}=-\dfrac{3}{5}\overline{a}+\dfrac{3}{5}\overline{b}$.
Huom! Jos suhde $3:2$ ymmärretty toisin päin ja tehtävä muuten oikein, niin -2 p.
Tarkastellaan kolmiota $ABC$. Piste $P$ jakaa kolmion sivun $AB$ suhteessa $1:3$, ja piste $Q$ jakaa kolmion sivun $BC$ suhteessa $1:3$. Missä suhteessa janojen $CP$ ja $AQ$ leikkauspiste $R$ jakaa janat?
Piirretään kuva. (1 p. )

Valitaan kolmiosta kaksi sivua ja määritetään niistä sivuvektorit, esim. $\overline{AB}=\overline{a}$ ja $\overline{AC}=\overline{b}$. Kaksi vektoria riittää, koska kolmas sivu voidaan lausua näiden kahden avulla. Otetaan tarkasteluun jompikumpi janoista $CP$ tai $AQ$. Tarkastellaan esimerkiksi janaa $CP$. Tehtävänä on selvittää, miten piste $R$ jakaa janan $CP$, eli vektoreiden avulla kysymys kuuluu, millä luvulla vektoria $\overline{CP}$ pitää kertoa, että saadaan vektori $\overline{CR}$. Esimerkiksi jos saataisiin $\overline{CR}=\dfrac{5}{7}\overline{CP}$, niin piste $R$ jakaisi janan $CP$ suhteessa $5:2$. Tutkitaan siis vektoria $\overline{CR}$.
Yritetään lausua vektori $\overline{CR}$ vektoreiden $\overline{a}$ ja $\overline{b}$ avulla. Koska piste $R$ on janalla $CP$, niin $$\overline{CR}=t\overline{CP}. \text{ (1 p.)}$$ Ilmoitetaan nyt $\overline{CP}$ eri tavalla. Saadaan $$\overline{CP}=\overline{CA}+\overline{AP},$$ josta edelleen sieventämällä saadaan $$\overline{CP}=-\overline{AC}+\dfrac{1}{4}\overline{AB}=-\overline{b}+\dfrac{1}{4}\overline{a}. \text{ (1 p.)}$$ Sijoittamalla tämä vektorin $\overline{CR}$ lausekkeeseen saadaan $$\overline{CR}=t\overline{CP}=-t\overline{b}+\dfrac{1}{4}t\overline{a}=\dfrac{1}{4}t\overline{a}-t\overline{b}.$$
Jotta tuntematon $t$ saadaan selvitettyä, pitää saada aikaiseksi yhtälö. Yritetään lausua vektori $\overline{CR}$ jollain toisella tavalla, mutta käyttämällä siinäkin vain vektoreita $\overline{a}$ ja $\overline{b}$. Saadaan $$\overline{CR}=\overline{CA}+\overline{AR}.$$ Muokataan tätä reittiä. Saadaan
\(\begin{align} \overline{CR}&=\overline{CA}+\overline{AR}=-\overline{AC}+s\overline{AQ}=-\overline{b}+s(\overline{AB}+\overline{BQ})\\ &=-\overline{b}+s(\overline{a}+\dfrac{1}{4}\overline{BC})=-\overline{b}+s(\overline{a}+\dfrac{1}{4}(\overline{BA}+\overline{AC}))\\ &=-\overline{b}+s(\overline{a}-\dfrac{1}{4}\overline{a}+\dfrac{1}{4}\overline{b})=-\overline{b}+\dfrac{3}{4}s\overline{a}+\dfrac{1}{4}s\overline{b}\\ &=\dfrac{3}{4}s\overline{a}+(\dfrac{1}{4}s-1)\overline{b}. \text{ (1 p.)} \end{align}\)
Nyt meillä on kaksi eri esitystapaa samalle vektorille käyttäen vektoreita $\overline{a}$ ja $\overline{b}$, toisin sanoen $$\overline{CR}=\dfrac{1}{4}ta-t\overline{b}=\dfrac{3}{4}s\overline{a}+(\dfrac{1}{4}s-1)\overline{b}$$. Luvussa Geometriaa vektoreiden avulla olevan teoreeman perusteella tämä tarkoittaa, että vektoreiden $\overline{a}$ ja $\overline{b}$ kertoimien pitää olla samat, joten saadaan yhtälöpari
\(\begin{cases} \dfrac{1}{4}t&=\dfrac{3}{4}s\\ -t&=\dfrac{1}{4}s-1, \end{cases}\)
jonka ratkaisuksi saadaan laskimella $t=\dfrac{12}{13}$ ja $s=\dfrac{4}{13}$. (1 p.)
Kun sijoitetaan saadut luvut vektoreihin $\overline{CR}=t\overline{CP}$ ja $\overline{AR}=s\overline{AQ}$, niin saadaan $$\overline{CR}=\dfrac{12}{13}\overline{CP}$$ ja $$\overline{AR}=\dfrac{4}{13}\overline{AQ}.$$
Vastaus: Piste $R$ jakaa janan $CP$ suhteessa $12:1$, ja janan $AQ$ suhteessa $4:9$. (1 p.) (Tämä näyttää kuvankin perusteella järkevältä.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
