Teoria
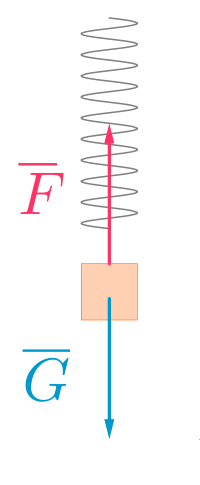
Ripustetaan punnus jouseen roikkumaan ja odotetaan, että punnus on levossa.
Punnukseen vaikuttaa ainoastaan punnuksen paino \(G\) ja jousivoima \(F\).
Tasapainotilanteessa punnus on levossa jolloin punnukseen vaikuttava kokonaisvoima on nolla.
Newtonin 2. lain mukaan
\(\begin{align} \sum \overline{F}&=0 \\ \overline{F}+\overline{G}&=0 \\ F&=G \end{align}\)
Ripustetaan jouseen erimassaisia punnuksia ja tutkitaan jousen venymää.
Punnuksen paino \(G\) on yhtä suuri kuin jousen punnukseen kohdistama jousivoima \(F\).
Sijoitetaan mittaustulokset \((x, \ F)-\)koordinaatistoon, jossa \(x\) on jousen venymä ja \(F\) on punnukseen kohdistuva jousivoima.
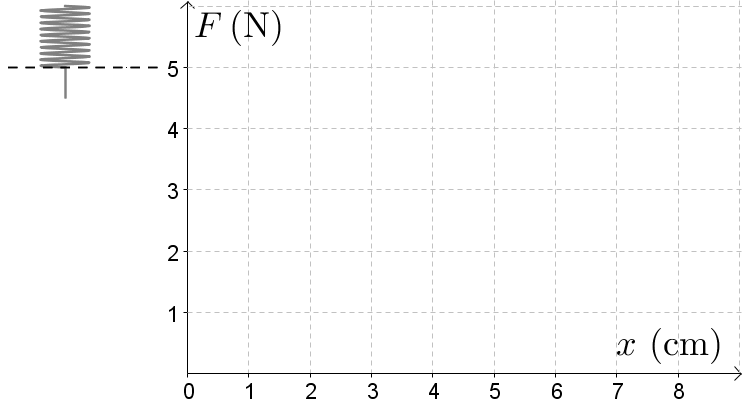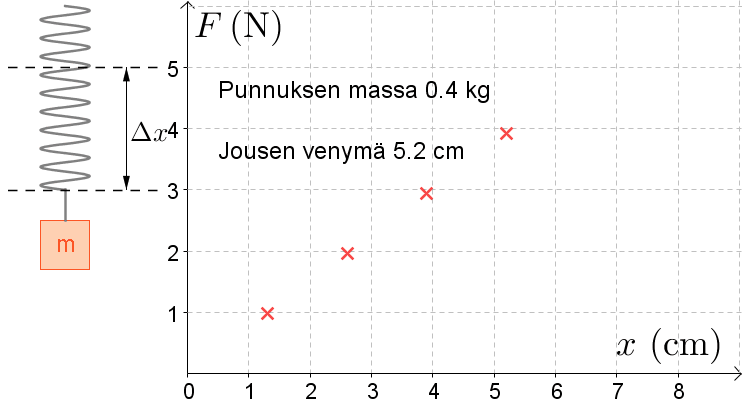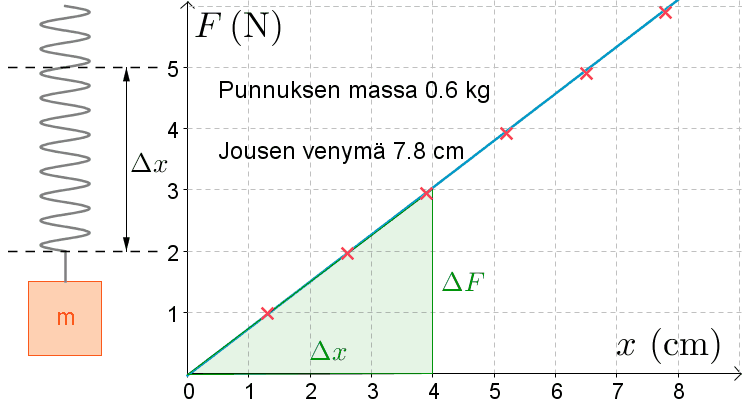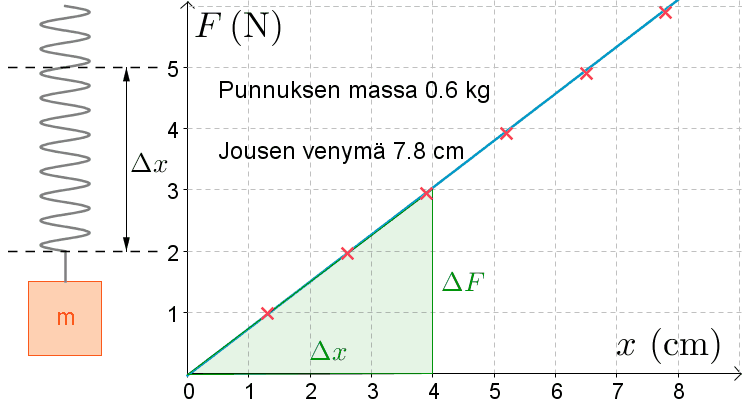
Huomataan, että jousivoima \(F\) ja jousen venymä \(x\) ovat suoraan verrannollisia eli \(F=k \cdot x\).
Ratkaistaan suoran fysikaalinen kulmakerroin.
\(k=\dfrac{\Delta F}{\Delta x}=\dfrac{3,0 \text{ N}}{0,04 \text{ m}}=75 \text{ N/m}\)
\((x, \ F)-\)koordinaatistoon piirretyn suoran fysikaalinen kulmakerroin on jousen jousivakio, joka kuvaa jousen jäykkyyttä.
Mitä suurempi jousivakion arvo on, niin sitä jäykempi jousi on.
Jousivoima on esimerkki harmonisesta voimasta.
Harmonisen voiman aiheuttamaa liikettä sanotaan harmoniseksi värähdysliikkeeksi.
