Testi on tarkoitettu kisallioppiminen.fi -sivuston MAY1-kurssin funktioluvun itsearviointiin.
Ohessa on erään funktion $f$ kuvaaja. Vastaa kuvaajan avulla seuraaviin kysymyksiin.
a) Määritä $f(-1)$ ja $f(0)$.
b) Määritä funktion $f$ nollakohdat.
c) Millä muuttujan $x$ arvoilla on $f(x)=1$? Anna vastaus yhden desimaalin tarkkuudella.
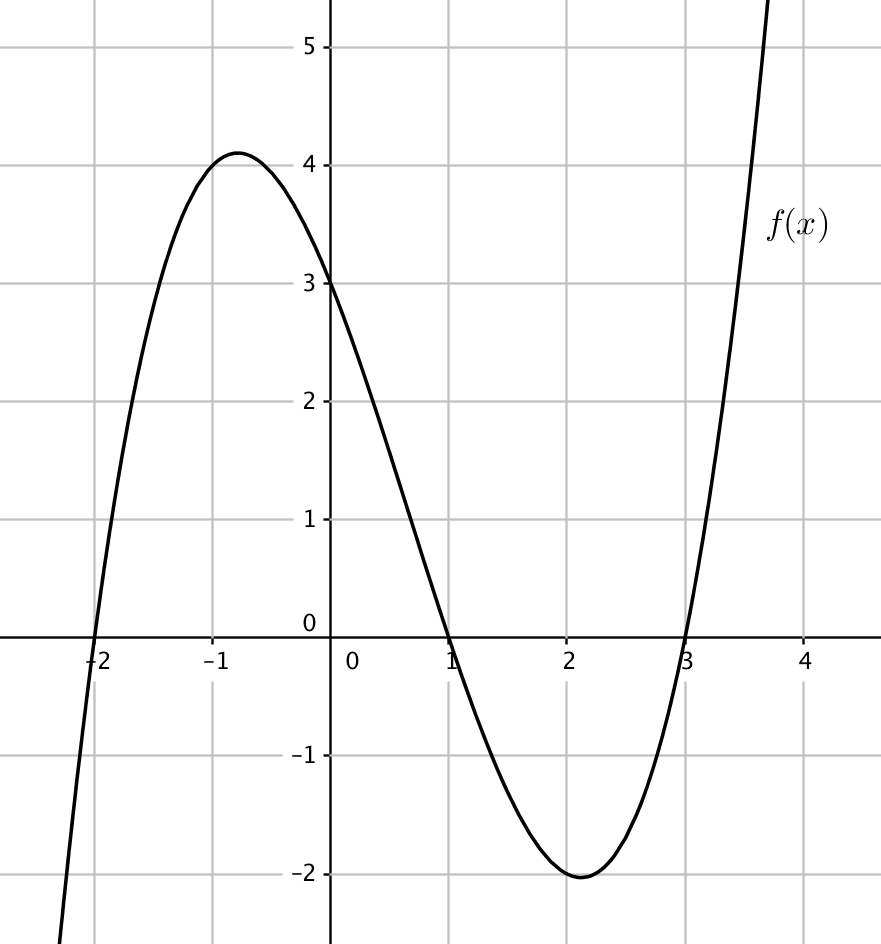
a) $f(-1)=4$ (1 p.) ja $f(0)=3$ (1 p.)
b) Funktion nollakohdat, eli ne muuttujan $x$ arvot, joilla funktio saa arvon nolla, ovat $x=-2$, $x=1$ ja $x=3$. (1 oikein 1 p., kaikki oikein 2 p.)
c) $f(x)=1$, kun $x\approx-1{,}8$, $x\approx0{,}6$ tai $x\approx3{,}2$. (1 oikein 1 p., kaikki oikein 2 p. Yhden desimaalin heitto sallitaan.)
Tarkastele funktiota $f(x)=\dfrac{x-2}{x+1}$. Käytä laskinta apunasi seuraavissa kohdissa.
a) Mitkä ovat funktion $f$ nollakohdat?
b) Millä korkeudella funktion $f$ kuvaaja leikkaa $y$-akselin?
c) Millä muuttujan $x$ arvoilla funktio $f$ on määritelty?
Tehtävän voi ratkaista joko piirtämällä funktion kuvaajan laskimella ja analysoimalla kuvaajaa tai määrittelemällä laskinsovelluksen puolella funktio $f(x)$ ja selvittämällä siellä esimerkiksi nollakohdat komennolla solve(f(x)=0,x). Laskinsovelluksen maininnat koskevat Texasin Nspire CX CAS -laskinta.
a) Kuvaajassa funktion nollakohdat ovat $x$-akselin leikkauspisteiden $x$-koordinaatit, laskinsovelluksessa yhtälön $f(x)=0$ ratkaisut. Funktion $f(x)$ nollakohta on $x=2$. (2 p.)
b) Funktion $f(x)$ kuvaaja leikkaa $y$-akselin korkeudella $y=-2$. Laskinsovelluksen puolella tämä selviää määrittämällä $f(0)$, joka on siis $-2$. (2 p.)
c) Kuvaajassa funktion määrittelyjoukko selviää katsomalla, millä muuttujan $x$ arvoilla kuvaaja näkyy. Laskinsovelluksen puolella tämän saa tehtyä tarkemmin komennolla domain(f(x),x). Funktio $f$ on määritelty, kun $x\neq-1$ tai toisin sanottuna kun $-\infty<x<-1$ tai $-1< x< \infty$. (2 p.)
Ohessa on neljän funktion kuvaajat. Valitse jokaiselle oikea lauseke alla olevista vaihtoehdoista. (1 oikein 1 p., 2 oikein 2 p., 3 oikein 4 p., kaikki oikein 6 p.)
a) $\left(\dfrac{1}{2}\right)^x$
b) $2^x$
c) $\dfrac{1}{2}x-1$
d) $-x+1$
e) $\dfrac{1}{2}x+1$
f) $\log_2 x$
g) $-2x+1$
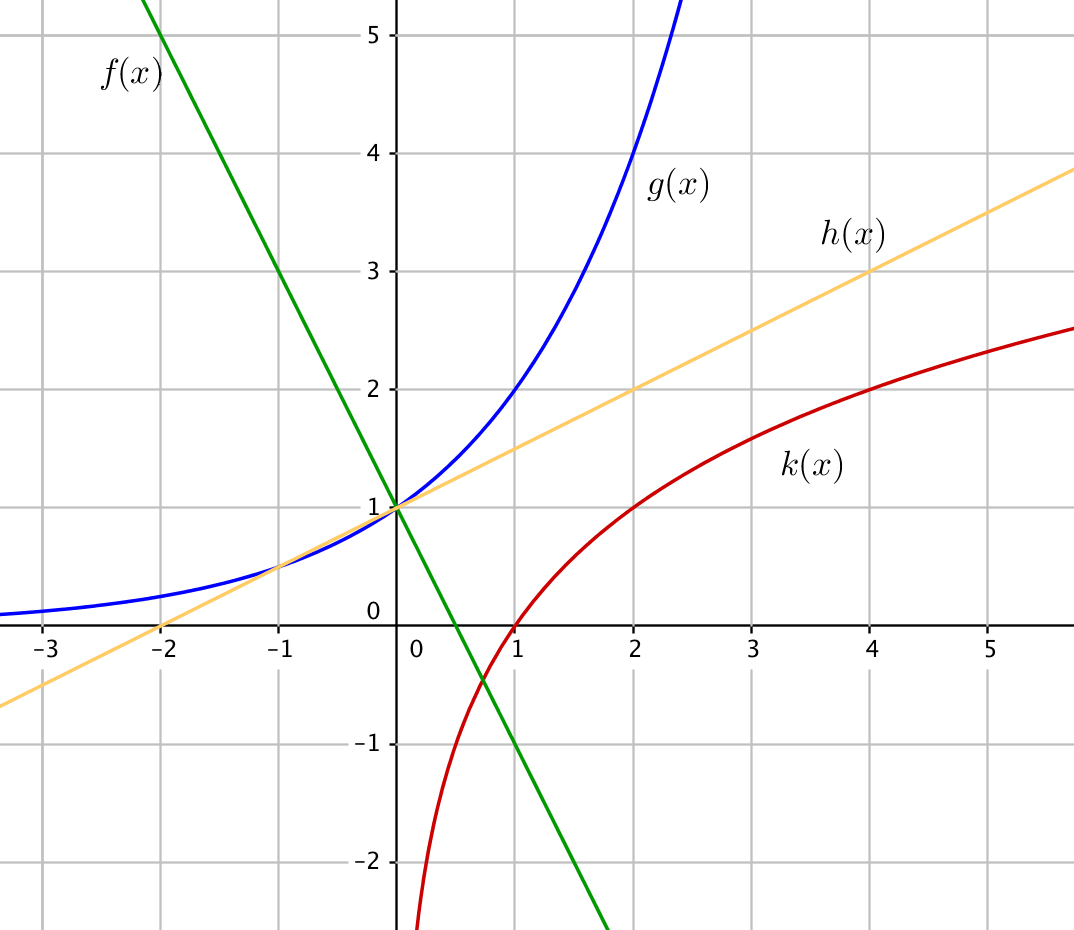
$f(x)=-2x+1$
$g(x)=2^x$
$h(x)=\dfrac{1}{2}x+1$
$k(x)=\log_2 x$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
