Testi on tarkoitettu kisallioppiminen.fi-sivun MAA2-kurssin itsearviointiin.
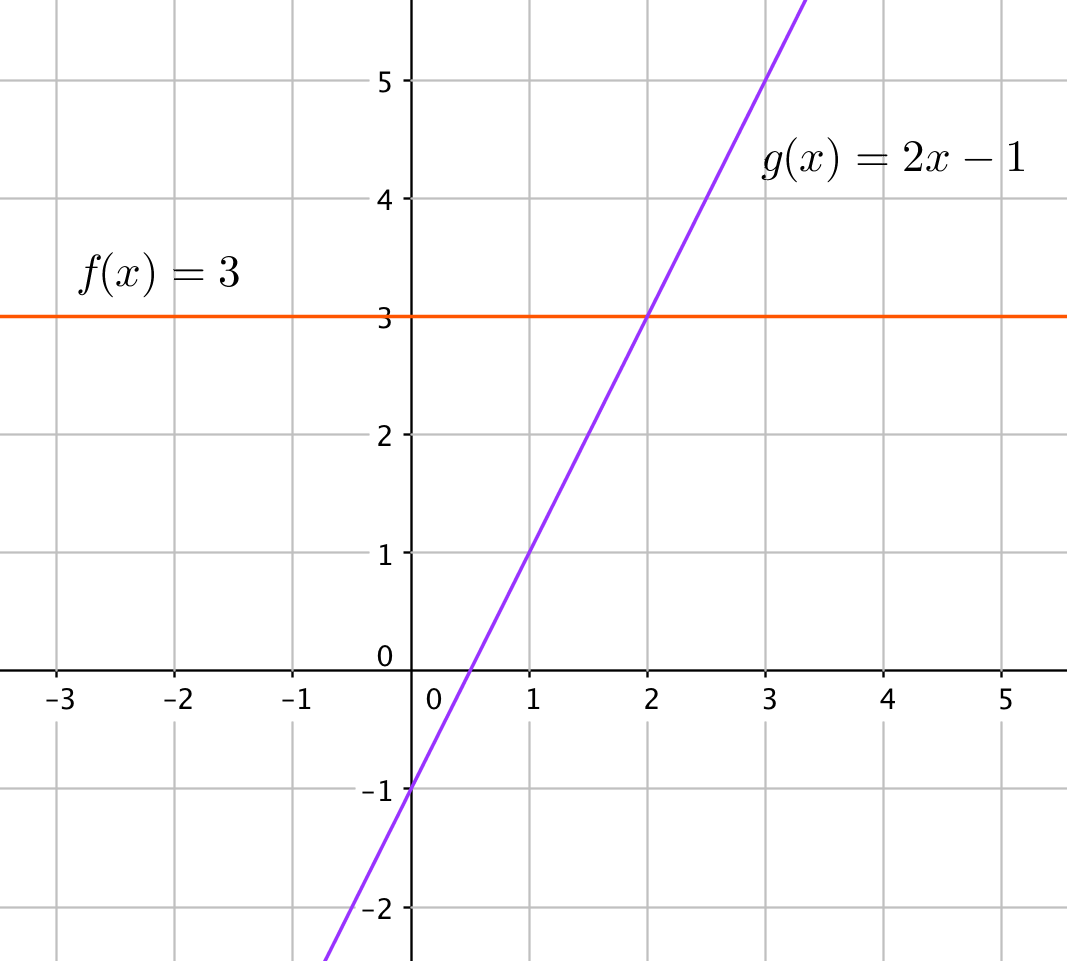
a) Piirrä ilman laskinta funktioiden $f(x)=3$ ja $g(x)=2x-1$ kuvaajat. Ennen pisteytysohjeen avaamista tarkista kuvaajasi laskimella ja jos huomaat virheen, niin päättele, mistä virhe johtui.
b) Ohessa on erään ensimmäisen asteen polynomifunktion $f$ kuvaaja. Muodosta kuvan avulla funktion $f$ lauseke. Piirrä sen jälkeen funktion $f$ kuvaaja laskimella ja tarkista, näyttääkö samalta kuin tehtävänannossa. Jos ei, niin muokkaa lauseketta.

a) Funktion $f(x)=3$ kuvaaja oikein. (1 p.)
Funktion $g(x)=2x-1$ kuvaaja leikkaa $y$-akselin pisteessä $(0,-1)$. (1 p)
Funktion $g(x)=2x-1$ kuvaajan kulmakerroin on oikein, eli siirtyessä yhden ruudun oikealle siirrytään kaksi ruutua ylös. (1 p.)
b) Koska suora leikkaa $y$-akselin korkeudella $y=2$, niin funktion $f(x)=ax+b$ kerroin $b$ on $b=2$. (1 p.)
Koska suora on laskeva, niin kerroin $a$ on negatiivinen, eli $a<0$. (1 p.)
Koska siirryttäessä kolme ruutua oikealle siirrytään yksi ruutu alas, niin suoran kulmakerroin on $-\dfrac{1}{3}$, eli $a=-\dfrac{1}{3}$.
Funktion $f$ lauseke on siis $f(x)=-\dfrac{1}{3}x+2$. (1 p.)
a) Ratkaise yhtälö $2x-1=-3x+3$.
b) Ratkaise yhtälö $x-\dfrac{2x-1}{3}=\dfrac{5x}{6}$.
c) Ratkaise epäyhtälö $3x\geq 5x-4$.
a) Muokataan yhtälöä.
\(\begin{align*} 2x-1&=-3x+3 \qquad &||&\ +3x\\ 2x-1+3x&=3\, &\, \\ 5x-1&=3 \qquad &||& \ +1\\ 5x&=3+1\,&\,&\, \\ 5x&=4 \qquad &||&\, :5\\ x&=\dfrac{4}{5}.\,&\,&\end{align*}\)
Tilanteesta $5x=4$ tai $-5x=-4$ (1 p.), vastaus $x=\dfrac{4}{5}$ (1 p.)
b) Periaate tässäkin yhtälössä on täysin sama, eli tavoite on saada kirjaimet $x$ toiselle puolelle yhtäsuuruusmerkkiä ja luvut toiselle puolelle. Yhtälön ratkaisun tekee haastavammaksi yhtälössä esiintyvät nimittäjät, joiden kanssa kannattaa edetä rauhassa, jottei tule merkkivirheitä tmv.
Muokataan yhtälöä.
\(\begin{align*} x-\dfrac{2x-1}{3}&=\dfrac{5x}{6} \quad &||& \, \text{Lavennetaan termit samannimisiksi.}\\ \dfrac{6x}{6}-\dfrac{2(2x-1)}{6}&=\dfrac{5x}{6} \quad &||& \, \text{Kerrotaan nimittäjät pois kertomalla yhtälöä puolittain luvulla }6.\\ 6x-2(2x-1)&=5x \, &\, &\\ 6x-4x+2&=5x \, &\, &\\ 2x+2&=5x \quad &||&\, -5x\\ 2x+2-5x&=0 \, &\, &\\ -3x+2&=0 \quad &||& \, -2\\ -3x&=-2 \quad &||& \, :(-3)\\ x&=\dfrac{-2}{-3}=\dfrac{2}{3}. \end{align*}\)
Tilanteesta, jossa termit on lavennettu samannimisiksi (1 p.), vastauksesta $x=\dfrac{2}{3}$ (1 p.)
Huom. Jos olisi kertonut toisella rivillä sulut auki $\dfrac{2(2x-1)}{6}=\dfrac{4x-2}{6}$, olisi pitänyt muistaa laittaa sulut seuraavalle riville, kun nimittäjät on kerrottu pois. Tyypillisin virhe on, että nimittäjien kertomisen jälkeen olisi päätynyt vaiheeseen $6x-4x-2=5x$, jolloin ei olisi vähentänyt koko lauseketta $4x-2$, vaan vain termin $4x$. Toinen tyypillinen virhe on, että ei muista laventaa termiä $x$ alussa ja tämän jälkeen kun kertoo yhtälöä kuudella, ei myöskään kerro kyseistä termiä kuudella, vaan päätyy tilanteeseen $x-2(2x-1)=5x$.
c) 1. asteen epäyhtälöt ratkaistaan kuten vastaavat yhtälöt, mutta jos kerrotaan tai jaetaan negatiivisella luvulla, niin epäyhtälömerkin suunta kääntyy. Muokataan epäyhtälöä.
\(\begin{align*} 3x&\geq 5x-4 \quad &||&\, -5x\\ 3x-5x&\geq -4 \, &\, &\\ -2x&\geq -4 \quad &||& \, :(-2)<0\\ x&\leq \dfrac{-4}{-2}\, & \, &\\ x&\leq 2. \end{align*}\)
Tilanteesta $-2x\geq -4$ tai $2x\leq 4$ (1 p.), vastauksesta $x\leq 2$. (1 p.)
a) Sievennä $\left(2x^2-3x+1\right)+\left(x^2-3\right)$. (1 p.)
b) Sievennä $\left(2x^2-3x+1\right)-\left(x^2-3\right)$. (2 p.)
c) Sievennä $\left(3x^2-x\right)\left(2x+1\right)$. (2 p.)
d) Erota yhteinen tekijä, eli lausu tulomuodossa $3x^2+5x$. (1 p.)
a) $\left(2x^2-3x+1\right)+\left(x^2-3\right)=2x^2-3x+1+x^2-3=3x^2-3x-2$ (1 p.)
b) $\left(2x^2-3x+1\right)-\left(x^2-3\right)=2x^2-3x+1-x^2+3$ (1 p.) Jatkamalla sievennystä saadaan $x^2-3x+4$ (1 p.)
c) $\left(3x^2-x\right)\left(2x+1\right)=3x^2\cdot 2x+3x^2\cdot 1-x\cdot 2x-x\cdot 1$ (1 p.), josta jatkamalla sievennystä saadaan $6x^3+3x^2-2x^2-x=6x^3+x^2-x$.(1 p.)
d) $3x^2+5x=x(3x+5)$ (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
