Testi on tarkoitettu kisallioppiminen.fi -sivun Toisen asteen polynomifunktio -luvun itsearviointiin.
a) Sievennä muistikaavojen avulla ilman laskinta. Älä siis avaa sulkeita perinteiseen tapaan, vaan tunnista, mikä muistikaavoista on kyseessä ja sovella kaavaa näihin tapauksiin. Tarkista kertomalla sulut auki perinteisesti tai laskimella ennen pisteytysohjeen katsomista.
$(x-3)(x+3)$
$(2x+1)^2$
$(\frac{1}{4}x-2)^2$
b) Jaa tekijöihin. Palauta aluksi mieleen, mitä keinoja tekijöihinjakoon on käytettävissä.
$3x^2+6x$
$x^2-4x+4$
$9x^2-4$
a) $(x-3)(x+3)=x^2-3^2$, (1/2 p.) josta saadaan $x^2-9$ (1/2 p.)
$(2x+1)^2=(2x)^2+2\cdot 2x\cdot 1+1^2$, (1/2 p.) josta saadaan $4x^2+4x+1$ (1/2 p.)
$(\frac{1}{4}x-2)^2=\left( \frac{1}{4}x\right)^2-2\cdot \frac{1}{4}x\cdot 2+2^2$, (1/2 p.) josta saadan $\frac{1}{16}x^2-x+4$ (1/2 p.)
b) $3x^2+6x=3x(x+2)$ (1 p.) Myös $x(3x+6)$ kelpaa.
$x^2-4x+4=x^2-2\cdot x\cdot2+2^2=(x-2)^2$ (1 p.)
$9x^2-4=(3x)^2-2^2$, (1/2 p.) josta saadaan $(3x+2)(3x-2)$ (1/2 p.)
a) Ratkaise yhtälö $x^2=2x$ kahdella eri tavalla. (3 p.)
b) Ratkaise yhtälö $-x^2+x=-2$. (2 p.)
c) Toisen asteen polynomilla $f$ on nollakohdat $x=-2$ ja $x=3$ ja sen kuvaaja on alaspäin aukeava paraabeli. Ratkaise epäyhtälö $f(x)<0$. (1 p.)
a) \(\begin{align*} x^2&=2x \\ x^2-2x&=0\\ x(x-2)&=0 \end{align*}\)
Tulon nollasäännön nojalla ainakin toisen tulontekijöistä on oltava nolla, eli saadaan yhtälöt
$x=0$ tai $x-2=0$, eli $x=2$.
Toisaalta ratkaisukaavaa käytettäessä yhtälö pitää olla muodossa $x^2-2x=0$, eli $a=1, b=-2$ ja $c=0$. Sijoittamalla ratkaisukaavaan saadaan
\(\begin{align*} x&=\dfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot1\cdot 0}}{2\cdot 1}\\ x&=\dfrac{2\pm\sqrt{4}}{2}\\ x&=\dfrac{2\pm2}{2}\\ x&=\dfrac{2+2}{2}=\dfrac{4}{2}=2 \text{ tai }x=\dfrac{2-2}{2}=\dfrac{0}{2}=0. \end{align*}\)
Kolmas tapa olisi täydentää vasen puoli $x^2-2x$ neliöksi, jolloin saataisiin
\(\begin{align*} x^2-2x&=0 \, &\, &\\ x^2-2\cdot x\cdot 1&=0 \qquad &||&\ \text{Kertoimen }b \text{ on oltava siis yksi. }+1^2 \\ x^2-2x+1^2&=0+1^2 \, &\, &\\ (x-1)^2&=1\, &\, &\\ x-1&=\pm\sqrt{1} \, &\, &\\ x-1&=\pm1\, & \, &\\ x&=1+1=2 \quad \text{ tai } &x&=-1+1=0. \end{align*}\)
Yksi ratkaisu oikein (2 p.), toinen ratkaisu oikein (1 p.)
b) $-x^2+x=-2$, johon lisäämällä yhtälön molemmille puolille $2$ saadaan $-x^2+x+2=0$. Nyt voidaan sijoittaa ratkaisukaavaan ($a=-1, b=1, c=2$). Saadaan
\(\begin{align*} x& = {-b \pm \sqrt{b^2-4ac} \over 2a}\\ x&=\dfrac{-1\pm\sqrt{1^2-4\cdot (-1)\cdot 2}}{2\cdot (-1)}\\ x&=\dfrac{-1\pm\sqrt{9}}{-2}\\ x&=\dfrac{-1\pm3}{-2}\\ x&=\dfrac{-1+3}{-2}=\dfrac{2}{-2}=-1 \text{ tai }x=\dfrac{-1-3}{-2}=\dfrac{-4}{-2}=2. \end{align*}\)
Kertoimet $a,b$ ja $c$ oikein (1 p.) (Voisi olla myös $a=1,b=-1,c=-2$). Vastauksesta $x=-1$ tai $x=2$ (1 p.)
c) Hahmotellaan kuva nollakohtien sekä tiedon, että kuvaaja on alaspäin aukeava paraabeli, avulla.

Yhtälö $f(x)<0$ on tosi, kun $x<-2$ tai $x>3$. Kuvasta (1/2 p.), vastauksesta (1/2 p.)
Millä vakion $a$ arvoilla funktiolla $f(x)=2x^2-3ax+a$ on enintään yksi nollakohta?
Funktio $f(x)=2x^2-3ax+a$ on toisen asteen polynomi, joten sillä voi olla nolla, yksi tai kaksi nollakohtaa. Enintään yksi nollakohta tarkoittaa nolla tai yksi nollakohtaa. (1 p.)
Tämä tarkoittaa, että yhtälöllä $f(x)=0$ eli $2x^2-3ax+a=0$ saa olla nolla tai yksi ratkaisua. Toisen asteen yhtälön ratkaisujen lukumäärän määrää diskriminantti $D=b^2-4ac$. Jotta yhtälöllä on nolla tai yksi ratkaisua, niin pitää olla voimassa $D\leq 0$. Muodostetaan diskriminantti ja ratkaistaan epäyhtälö.
\(\begin{align*} D=b^2-4ac=(-3a)^2-4\cdot 2\cdot a=9a^2-8a\leq 0. \end{align*}\) (2 p.)
Ratkaistaan ne $a$:n arvot, joilla $9a^2-8a=0$ ja hahmotellaan sen jälkeen lausekkeen $9a^2-8a$ kuvaaja. Saadaan
\(\begin{align*} 9a^2-8a&=0\\ a(9a-8)&=0\\ a&=0 \text{ tai } 9a-8=0, \text{ josta } a=\dfrac{8}{9}. \end{align*}\) (1 p.)
Hahmotellaan kuva.
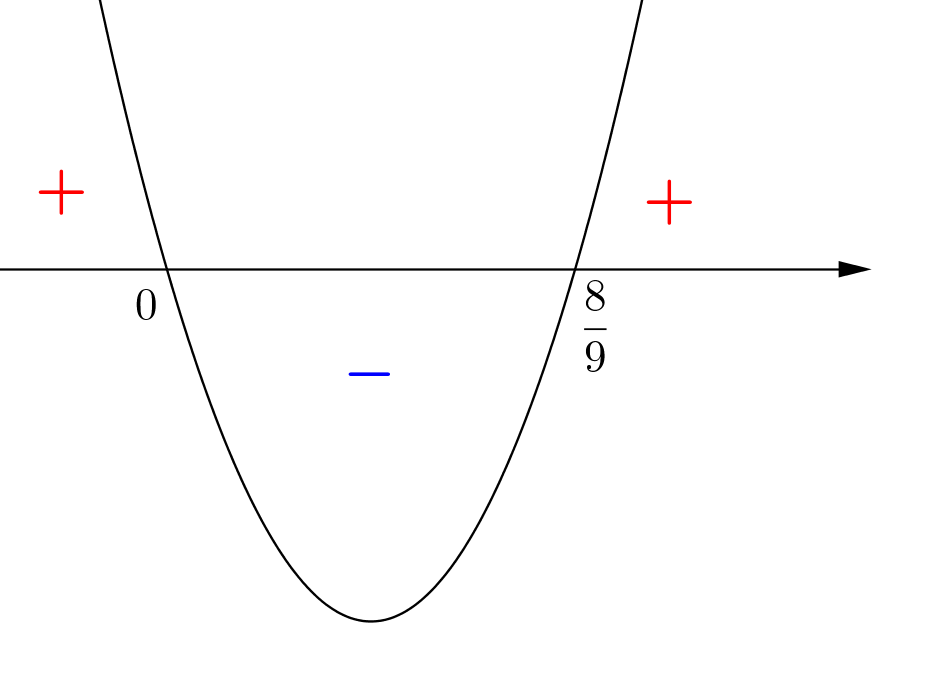
Kuva (1 p.)
Haluttiin, että $D=9a^2-8a\leq 0$, joten $0\leq a \leq \dfrac{8}{9}$. (Voi myös sanoa $a\geq 0$ ja $a\leq \dfrac{8}{9}$.) (1 p.)
Vastaus: Vakion $a$ arvoilla $0\leq a \leq \dfrac{8}{9}$.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
