Testi on tarkoitettu kisallioppiminen.fi -sivun MAA2-kurssin itsarviointiin.
a) Alla on kahden potenssifunktion $x^n$, jossa $n$ on positiivinen kokonaisluku, kuvaaja.
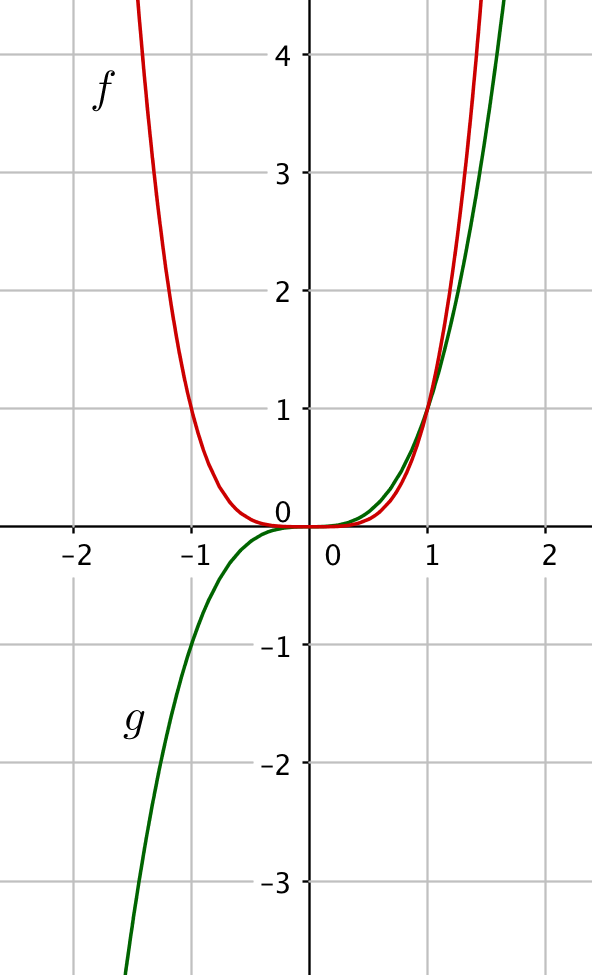
Kumpi kuvaajista on parittoman potenssifunktion (eli $n$ pariton) kuvaaja? Entä parillisen potenssifunktion? Perustele. (1 p.)
Kumpaan yhtälöön $f(x)=-1$ vai $g(x)=-1$ on olemassa kuvaajien perusteella ratkaisu? (1 p.)
Määritä kuvaajan perusteella ratkaisut yhtälöihin $f(x)=3$ ja $g(x)=3$ yhden desimaalin tarkkuudella. (1 p.)
b) Ratkaise yhtälö $\dfrac{1}{2}x^4=8$ ilman laskinta. (2 p.)
c) Sievennä lauseke $\sqrt{\sqrt[3]{3}}\sqrt[3]{3}$ (1 p.)
a) $f$ on parillisen, $g$ parittoman potenttifunktion kuvaaja (1/2 p.), koska pariton potenssifunktio saa myös negatiivisia arvoja (tai parillinen on symmetrinen $y$-akselin suhteen) (1/2 p.).
Yhtälöön $g(x)=-1$ on olemassa kuvaajan perusteella ratkaisu (1 p.), koska kyseinen funktio saa arvon $-1$, eli kulkee $x$-akselin alapuolella.
Kuvaajan perusteella $f(x)=3$, jos $x\approx 1{,}3$ tai $x\approx -1{,}3$. (1/2 p.) Vastaavasti $g(x)=3$, jos $x\approx 1{,}4$. (1/2 p.) Yhden desimaalin heitto hyväksytään.
b)
\(\begin{align*} \dfrac{1}{2}x^4&=8 \quad &|| \cdot 2\\ x^4&=16 \\ x&=\pm \sqrt[4]{16} \\ x&=2 \text{ tai } x=-2. \end{align*}\)Vaiheesta $x^4=16$ (1 p.), vastauksesta (1 p.). Jos puuttuu $\pm$, niin -1/2 p.
c) Juurilausekkeet on yksinkertaisinta sieventää murtopotenssien avulla. Lopuksi annetaan vastaus taas juurimuodossa.
$\sqrt{\sqrt[3]{3}}\sqrt[3]{3}=\left(3^{\frac{1}{3}}\right)^{\frac{1}{2}}\cdot 3^{\frac{1}{3}}$, (1/2 p.) josta potenssien laskusäännöillä saadaan
$3^{\frac{1}{3}\cdot \frac{1}{2}}\cdot 3^{\frac{1}{3}}=3^{\frac{1}{6}+\frac{1}{3}}=3^{\frac{1}{6}+\frac{2}{6}}=3^{\frac{3}{6}}=3^{\frac{1}{2}}=\sqrt{3}$. (1/2 p.)
a) Ratkaise yhtälö $x^3+3x^2+2x=0$ ilman laskinta.
b) Ratkaise yhtälö $4x^3+x^2-8x-2=0$ ilman laskinta.
c) Kolmannen asteen polynomilla $P(x)=2x^3-8x^2+6x$ on nollakohdat $x=0, x=1$ ja $x=3$. Jaa $P$ tekijöihin, eli lausu se sellaisessa tulomuodossa, jossa tulontekijät ovat mahdollisimman pientä astelukua.
a) \(\begin{align*} x^3+3x^2+2x&=0\\ x\left(x^2+3x+2\right)&=0 \\ x&=0 \text{ tai } &x^2+3x+2=&0\\ \, &\, \, &x=&\dfrac{-3\pm\sqrt{3^2-4\cdot 1\cdot 2}}{2\cdot 1}\\ \, &\, \, &x=&\dfrac{-3\pm\sqrt{1}}{2}\\ \, &\, \, &x=&\dfrac{-3\pm1}{2}\\ \, &\, \, &X=&\dfrac{-3+1}{2}=\dfrac{-2}{2}=-1 \text{ tai }x=\dfrac{-3-1}{2}=\dfrac{-4}{2}=-2. \end{align*}\) Yhteinen tekijä $x$ (1 p.), vastaus (1 p.)
Vastaus: $x=-2, x=-1$ tai $x=0$.
b) Koska yhtälöstä $4x^3+x^2-8x-2=0$ ei voi suoraan ottaa yhteistä tekijää, pitää yhtälön vasenta puolta ryhmitellä ensin. Saadaan esimerkiksi
$x^2(4x+1)-2(4x+1)=0$, (1/2 p.) josta voidaan yhteinen tekijä $(4x+1)$. Vasen puoli sievenee muotoon
$(4x+1)\left(x^2-2\right)=0$. (1/2 p.) Tulon nollasäännön nojalla saadaan yhtälön ratkaisuiksi
$4x+1=0$, eli $x=-\dfrac{1}{4}$ (1/2 p.) ja $x^2-2=0$, eli $x=\pm \sqrt{2}$ (1/2 p.)
Vastaus: $x=-\dfrac{1}{4}, x=-\sqrt{2}$ tai $x=\sqrt{2}$.
c) Koska polynomilla $P$ on nollakohdat $x=0, x=1$ ja $x=3$, niin sillä on tekijät $x-0=x, x-1$ ja $x-3$. (1 p.) Muita tekijöitä sillä ei ole. Lasketaan näiden tulo ja tutkitaan, saadaanko suoraan polynomi $P$ vai pitääkö lauseketta kertoa vielä jollain luvulla. Saadaan
$x(x-1)(x-3)=\left(x^2-x\right)(x-3)=x^3-3x^2-x^2+3x=x^3-4x^2+3x$. (1/2 p.) Huomataan, että saatu lauseke ei ole $P$, mutta kertomalla lauseketta luvulla $2$ saadaan lausekkeesta $P$. Polynomi $P$ on siis
$P(x)=2x^3-8x^2+6x=2x(x-1)(x-3)$. (1/2 p.)
Ratkaise epäyhtälö $x^3\leq 9x$ ilman laskinta.
Muokataan epäyhtälö muotoon, jossa toisella puolella epäyhtälöä on nolla. Saadaan
\(\begin{align*} x^3&\leq 9x \\ x^3-9x&\leq 0. \end{align*}\) (1 p.)
Ratkaistaan epäyhtälön vasemmalla puolella olevan lausekkeen nollakohdat.
\(\begin{align*} x^3-9x&=0\\ x\left(x^2-9\right)&=0\\ x&=0 \text{ tai } &x^2-9=&0\\ \,&\, &x^2=&9\\ \, &\, &x=&\pm\sqrt{9}=\pm3\\ \, &\, &x=&3 \text{ tai }x=-3. \end{align*}\) Yhteinen tekijä $x$ (1 p.), nollakohdat (1 p.)
Tehdään merkkikaavio. Merkkikaavioon pystyviivoiksi tulee lausekkeen nollakohdat, eli tässä tapauksessa $0,-3$ ja $3$. Lausekkeen $x^3-9x$ merkit voi perustella joko testipisteillä tai tulontekijöiden $x$ ja $x^2-9$ kuvaajilla.
1) Testipisteet: Valitaan jokaiselta väliltä $x<-3, -3<x<0, 0<x<3$ ja $x>3$ jokin luku ja sijoitetaan se lausekkeeseen. Lausekkeen arvo kertoo, onko lausekkeen arvot koko tarkasteluvälillä positiivisia vai negatiivisia. Esimerkiksi
$x=-4$: $(-4)^3-9\cdot (-4)=-48+36=-12<0$
$x=-1$: $(-1)^3-9\cdot (-1)=-1+9=8>0$
$x=1$: $1^3-9\cdot 1=1-9=-8<0$
$x=4$: $4^3-9\cdot 4=48-36=12>0$.
Merkkikaavioksi saadaan
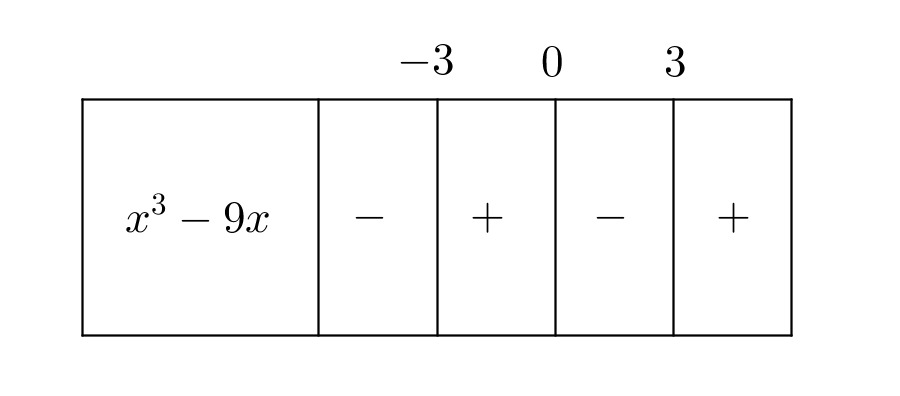
2) Hahmotellaan tulontekijöiden $x$ ja $x^2-9$ kuvaajat ja päätellän lopuksi tulon $x\left(x^2-9\right)$ merkki. Nyt merkkikaavio näyttää tältä:
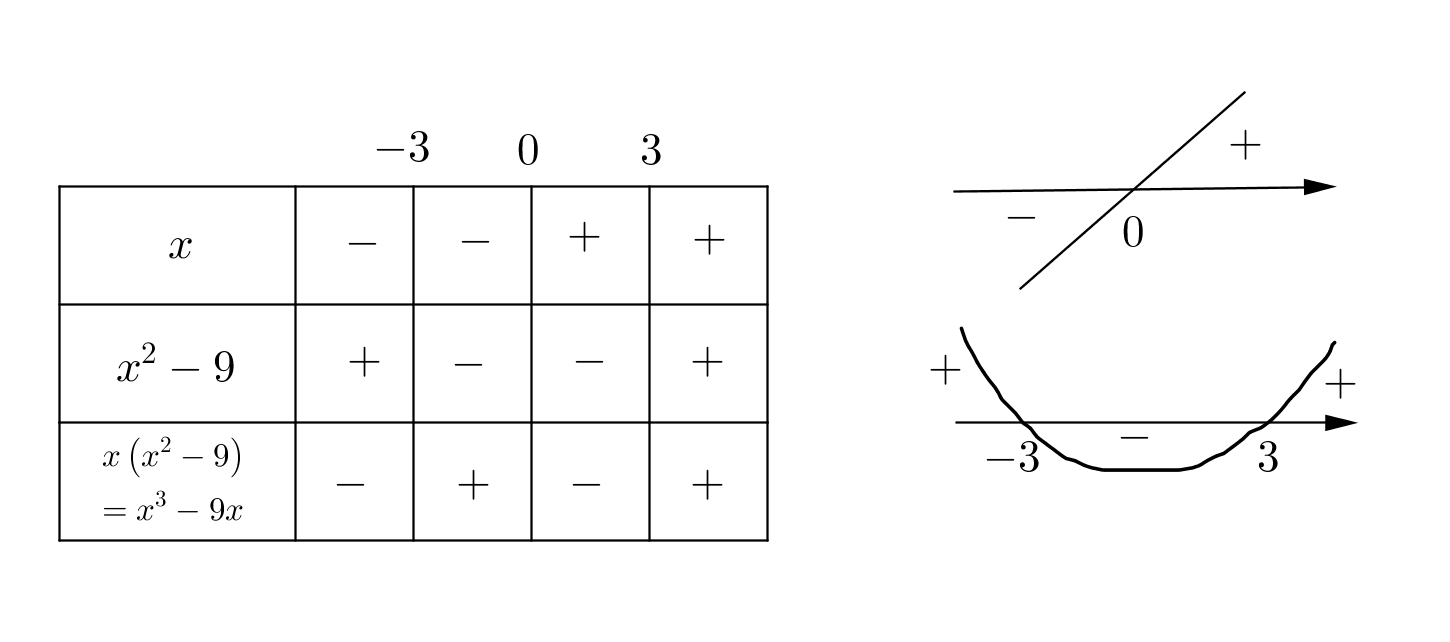
Kummastakin merkkikaaviosta perusteluineen yhteensä (2 p.), eli oikeat merkit polynomille $x^3-9x$ (1 p.) ja perustelut merkeille (1 p.)
Lopuksi merkkikaaviosta luetaan vastaus. Haluttiin, että $x^3-9x\leq 0$, joten katsotaan, millä muuttujan $x$ arvoilla merkkikaaviossa on miinus. Nollakohdat hyväksytään mukaan ratkaisuksi, koska niissä lauseke saa arvon nolla.
Vastaus: $x\leq -3$ tai $0\leq x\leq 3$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
