Testi on tarkoitettu kisallioppiminen.fi -sivun MAA3-kurssin itsearviointiin.
a) Suunnikkaan pinta-ala on 20 ja kannan pituus on 5. Suunnikkaan terävät kulmat ovat 30 astetta. Mikä on suunnikkaan toisen sivun pituus?
b) Tasasivuisen kolmion sivun pituutta lyhennetään 30 %. Kuinka monta prosenttia kolmion pinta-ala pienenee?
a) Hahmotellaan kuva.

Ratkaistaan suunnikkaan korkeus $h$.
$A=\text{kanta}\cdot \text{korkeus}=5h=20$, josta $h=4.$ (1 p.)
Suorakulmaisesta kolmiosta $BEC$ saadaan yhtälö $\sin 30^{\circ}=\dfrac{4}{x}$ (1 p.), josta $x=8$. (1 p.)
Vastaus: Suunnikkaan toinen sivu on 8.
b) Tasasivuiset kolmiot ovat yhdenmuotoisia, koska vastinkulmat ovat yhtä suuria (kaikkien tasasivuisten kolmioiden kulmat ovat 60 astetta.) (1 p.) Siis alkuperäinen ja pienennetty kolmio ovat yhdenmuotoisia, jolloin niiden pinta-alojen suhde on vastinsivujen suhteen neliö, eli mittakaavan neliö. Merkitään alkuperäisen kolmion sivun pituutta kirjaimella $x$ ja pinta-alaa kirjaimella $A$. Tällöin pienennetyn kolmion sivun pituus on $0{,}7x$. Merkitään pienennetyn kolmion pinta-alaa $A_p$. Saadaan verrantoyhtälö
\(\begin{align*} \left(\dfrac{0{,}7x}{x}\right)^2&=\dfrac{A_p}{A}\\ 0{,}7^2&=\dfrac{A_p}{A}\\ A_p&=0{,}49A. \end{align*}\) Yhtälö (1 p.)
Uusi pinta-ala on siis $49$ % alkuperäisestä, eli pinta-ala on pienentynyt $51$ %. (1 p.)
a) Ympyrän, jonka säde on 3, sektorin pinta-ala on $\frac{3}{2}\pi$. Laske sektoria vastaavan segmentin pinta-ala. Anna vastaus kahden merkitsevän numeron tarkkuudella.
b) Ratkaise kuvassa näkyvä kaaren pituus $b$ yhden desimaalin tarkkuudella.

a) Hahmotellaan kuva.

Ratkaistaan sektorin keskuskulma $\alpha$ sektorin pinta-alasta.
\(\begin{align*} A_{\text{sektori}}&=\frac{\alpha}{360^{\circ}}\cdot \pi r^2\\ \frac{3\pi}{2}&=\frac{\alpha}{360^{\circ}}\cdot \pi \cdot3^2\\ \frac{3\pi}{2}&=\frac{9\pi}{360^{\circ}}\cdot \alpha \qquad || \cdot \frac{360^{\circ}}{9\pi}\\ \alpha&=\frac{3\pi}{2}\cdot \frac{360^{\circ}}{9\pi}=60^{\circ}. \end{align*}\) Yhtälö (0,5 p.), keskuskulma (0,5 p.)
Segmentin pinta-ala saadaan sektorin ja kolmion $ABC$ erotuksesta. Sektorin pinta-ala tunnetaan, ratkaistaan kolmion $ABC$ pinta-ala kaavalla $A=\frac{1}{2}ab\sin \gamma$, jossa $a$ ja $b$ ovat kolmion vierekkäisten sivujen pituudet ja $\gamma$ on näiden sivujen välinen kulma. Kolmiosta $ABC$ saadaan
$A=\frac{1}{2}\cdot 3\cdot 3\cdot \sin 60^{\circ}=\frac{9\sqrt{3}}{4}.$ (1 p.)
Segmentin pinta-ala on näin ollen $A_{\text{segmentti}}=A_{\text{sektori}}-A_{\text{kolmio}}=\frac{3\pi}{2}-\frac{9\sqrt{3}}{4}=0{,}815\ldots\approx0{,}82$. (1 p.)
b) Kuvaan piirretyt janat ovat ympyrän tangentteja. Täydennetään kuvaa piirtämällä säteet kaaren päätepisteisiin sekä merkitsemällä kaarta vastaavaa keskuskulmaa kirjaimella $\beta$.

Tangenttikulman ja sitä vastaavan keskuskulman summa on $180^{\circ}$, joten $\beta=180^{\circ}-40^{\circ}=140^{\circ}$. (1 p.)
Kaaren pituus on $b=\frac{140^{\circ}}{360^{\circ}}\cdot 2\cdot \pi \cdot 2=4{,}88\ldots\approx4{,}9$. (Lauseke oikein (1 p.), vastaus (1 p.))
a) Kuinka kauas on mahdollista nähdä Stadionin tornista, joka on 72 m merenpinnan yläpuolella? Maapallon säde on noin 6370 km ja etäisyys mitataan maapallon pintaa pitkin.
b) Määritä kuvan kolmion sivun pituus $x$, kun ympyrän säde on $3{,}0$ m.
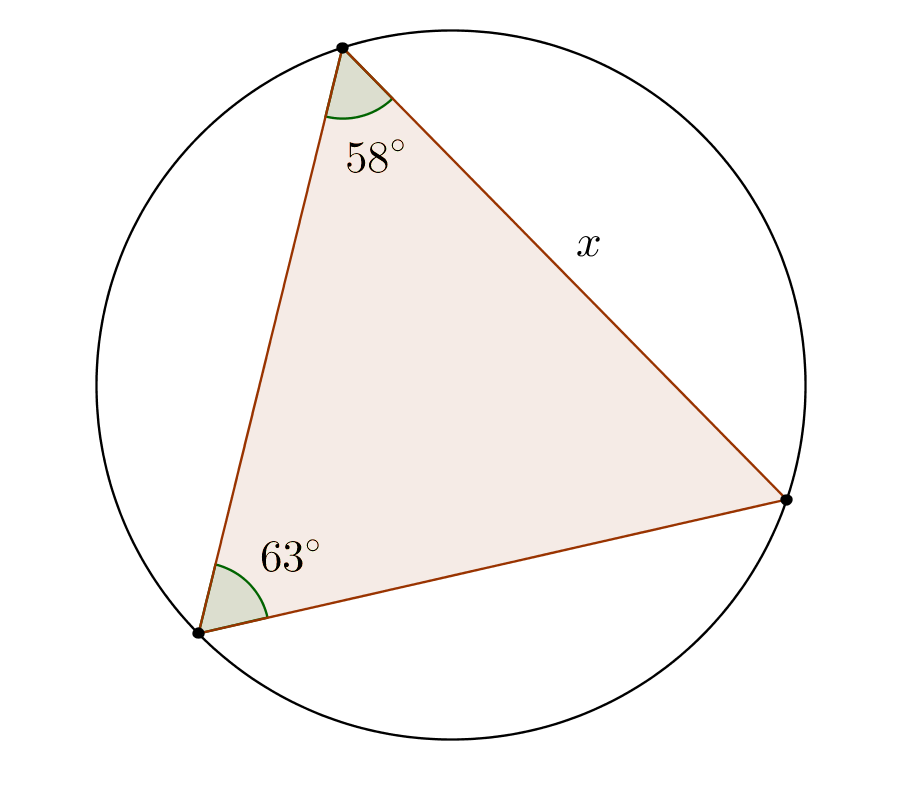
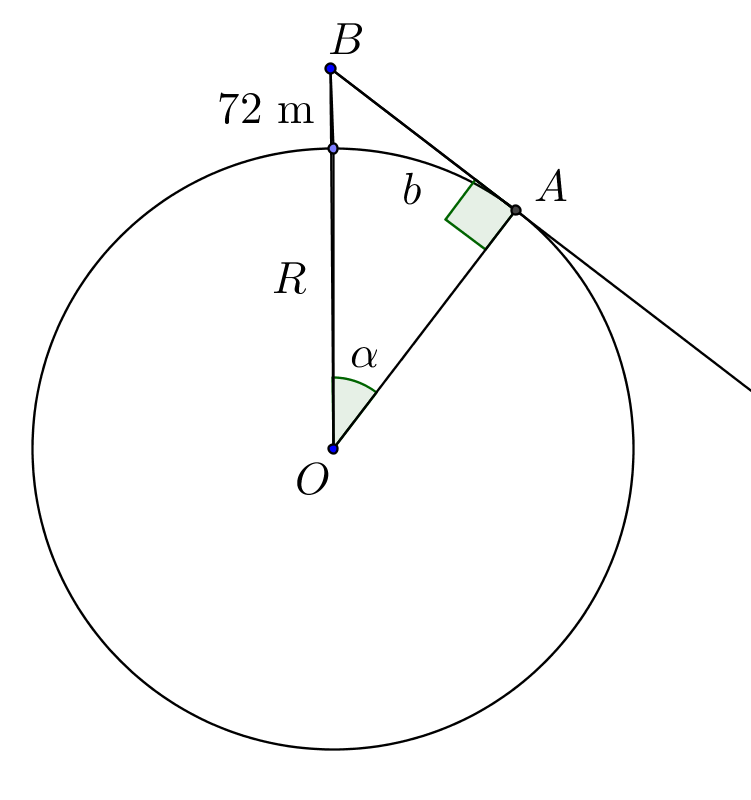
a) Hahmotellaan mallikuva.
 Kuva (1 p.)
Kuva (1 p.)
Maapallon säde on $R=6370$ km. Kun kuvan kulma $\alpha$ saadaan selvitettyä, niin tämän avulla saadaan laskettua kysytty kaaren pituus $b$. Muutetaan ensin $72$ m kilometreiksi. $72 \text{ m}=0{,}072 \text{ km}$. Suorakulmaisesta kolmiosta $OAB$ saadaan yhtälö
\(\begin{align*} \cos \alpha&=\frac{R}{R+0{,}072}\\ \cos \alpha&=\frac{6370}{6370{,}072}\\ \alpha&=0{,}272\ldots^{\circ}. \end{align*}\) (1 p.)
Kysytty etäisyys on kuvaan merkitty kaaren pituus $b$, joka on $$b=\frac{0{,}272\ldots^{\circ}}{360^{\circ}}\cdot 2\pi\cdot 6370=30{,}28\ldots \approx 30 \text{ (km)}.$$
Vastaus: Stadionin tornista voi nähdä 30 km päähän. (1 p.)
b) Tehtävänannon kolmion kärjet ovat ympyrän kehällä. Jokainen kolmion kulmista on kehäkulma. Valitaan tarkastelukohteeksi sivun $x$ vastainen kulma, eli $63^{\circ}$ asteen kulma. Täydennetään kuvaa.
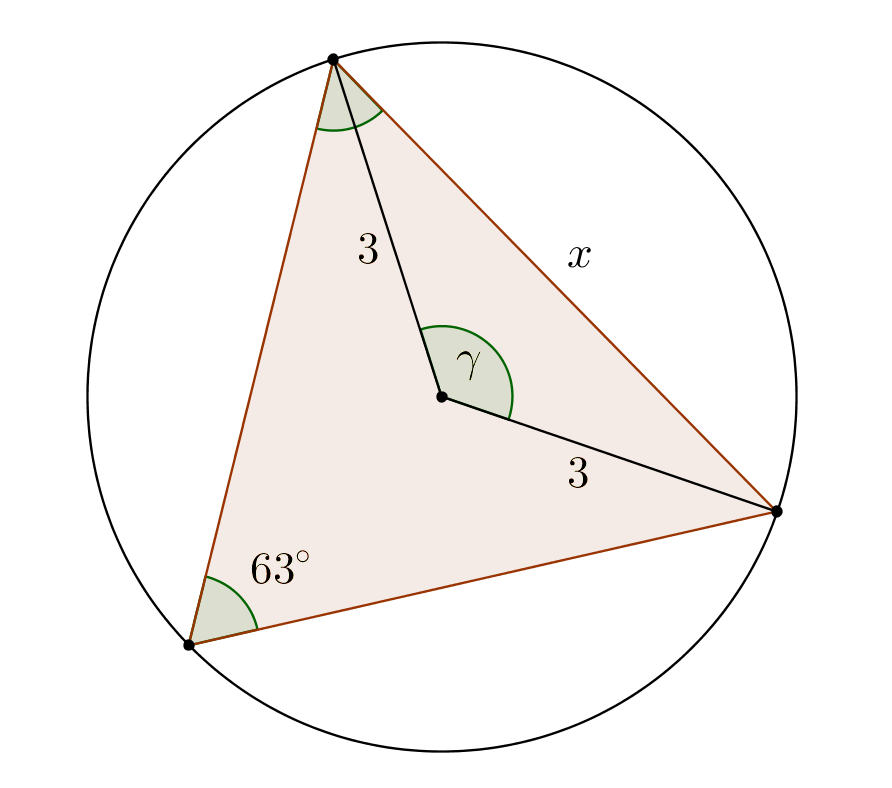
Kulma $\gamma$ saadaan kehäkulmalauseesta, joka sanoo, että kehäkulma on puolet samaa kaarta vastaavasta keskuskulmasta. Siis $63^{\circ}=\frac{1}{2}\gamma$, joten $\gamma=2\cdot 63^{\circ}=126^{\circ}$. (1 p.)
Kolmion sivun pituus $x$ saadaan kosinilauseella.
\(\begin{align*} x^2&=3^2+3^2-2\cdot 3\cdot 3\cdot \cos 126^{\circ}\\ x^2&=28{,}58\ldots\\ x&=\pm \sqrt{28{,}58\ldots} \quad ||\ x>0\\ x&=5{,}34\ldots\approx5{,}3 \text{ (m).} \end{align*}\) Yhtälö (1 p.)
Vastaus: Kolmion sivun pituus $x$ on $5{,}3$ m. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
