Testi on tarkoitettu kisallioppiminen.fi -sivun MAA3-kurssin itsearviointiin.
Suorakulmaisen särmiön mitat ovat suhteessa $2:3:4$ (lev., pit., kork.) ja sen tilavuus on $1500 \text{ m}^3$. Laske avaruuslävistäjän pituus kymmenen senttimetrin tarkkuudella.
Hahmotellaan kuva.
Ratkaistaan $x$ tilavuudesta saatavasta yhtälöstä.
\(\begin{align*} V&=2x\cdot 3x\cdot 4x\\ 24x^3&=1500 \qquad ||:24\\ x^3&=\frac{125}{2}\\ x&=\sqrt[3]{\frac{125}{2}}=\frac{5}{\sqrt[3]{2}} \text{ (m)}. \end{align*}\)Yhtälö (1 p.), vaiheesta $x^3=\frac{125}{2}$ (1 p.), $x$ oikein (1 p.)
Avaruuslävistäjä saadaan kaavalla $d^2=a^2+b^2+c^2$, missä $a,b$ ja $c$ ovat särmien pituudet. Saadaan
\(\begin{align*} d^2&=(2x)^2+(3x)^2+(4x)^2\\ d^2&=\left(2\cdot\frac{5}{\sqrt[3]{2}}\right)^2+\left(3\cdot\frac{5}{\sqrt[3]{2}}\right)^2+\left(4\cdot\frac{5}{\sqrt[3]{2}}\right)^2\\ d^2&=\frac{725}{\sqrt[3]{4}}\\ d&=\pm\sqrt{}\frac{725}{\sqrt[3]{4}} \qquad ||\ d>0\\ d&=21{,}37\ldots\approx21{,}4 \text{ (m)}. \end{align*}\\\) Yhtälö (1 p.), $d=21{,}37\ldots$ (1 p.)
Vastaus: Avaruuslävistäjän pituus on $21{,}4$ m. (1 p.)
Neliöpohjaisen suoran pyramidin pohjan pinta-ala on 64 ja korkeus 6.
a) Laske pyramidin tilavuus. (1 p.)
b) Laske pyramidin kokonaispinta-ala kolmen merkitsevän numeron tarkkuudella. (2 p.)
c) Laske sivusärmän ja pohjatahkon välinen kulma asteen tarkkuudella. (3 p.)
a) Kartion tilavuus on $V=\frac{1}{3}A_{\text{pohja}}\cdot \text{korkeus}=\frac{1}{3}\cdot 64\cdot 6=128$. (1 p.)
b) Hahmotellaan kuva, johon merkitään sivutahkon korkeutta kirjaimella $x$ ja pohjaneliön sivun pituutta kirjaimella $y$.
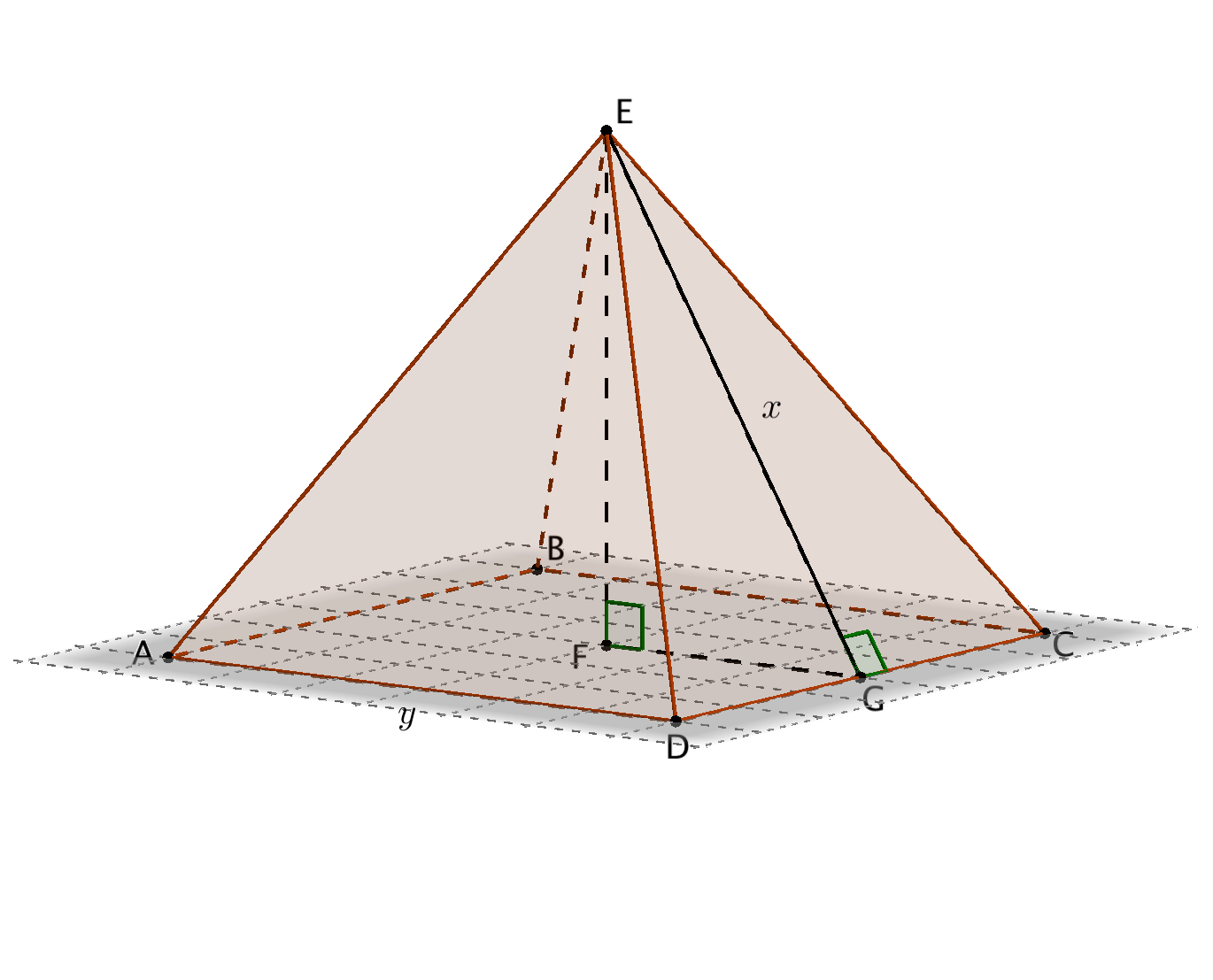
Ratkaistaan pohjaneliön sivun pituus pohjan pinta-alasta.
$y^2=64$, josta $y=8$ ($y>0$).
Suorakulmaisesta kolmiosta $FGE$ saadaan ratkaistua sivutahkon korkeus $x$. Pythagoraan lauseen nojalla saadaan
$4^2+6^2=x^2$, josta $x^2=52$ ja edelleen $x=\sqrt{52}(=2\sqrt{13})$. (1 p.)
Sivutahkon pinta-ala on $A_{\text{sivutahko}}=\frac{1}{2}\cdot 8\cdot \sqrt{52}=4\sqrt{52}$, jolloin kokonaispinta-ala on
$A_{\text{kok.}}=A_{\text{pohja}}+4A_{\text{sivutahko}}=64+4\cdot 4\sqrt{52}=64+16\sqrt{52}=179{,}37\ldots\approx179$. (1 p.)
c) Merkitään kuvaan kysytty kulma ja merkitään sitä $\alpha$.
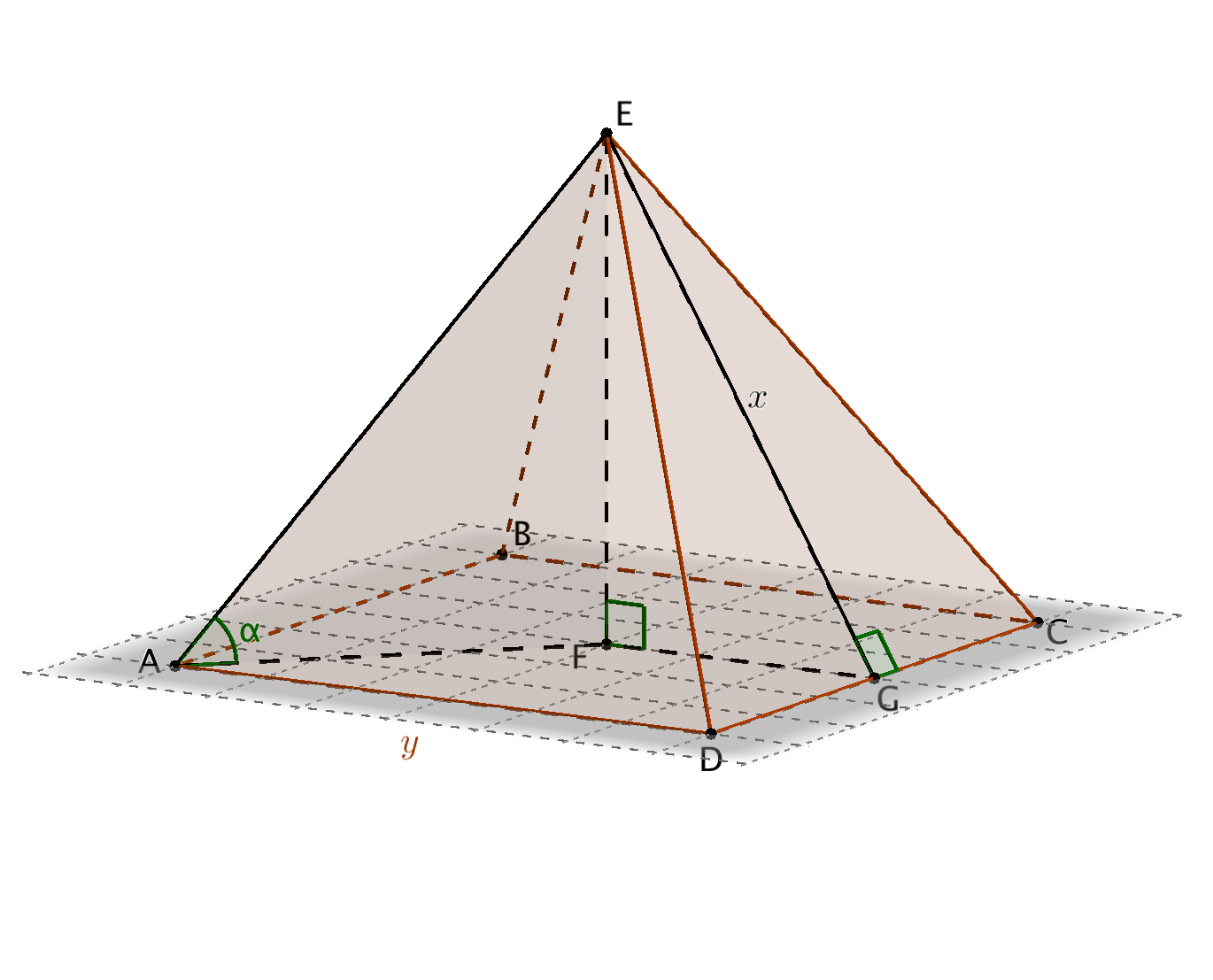 Kuva, jossa kulma merkitty oikein (1 p.).
Kuva, jossa kulma merkitty oikein (1 p.).
Kysytty kulma $\alpha$ on suorakulmaisen kolmion $AFE$ kulma. Kolmiosta tunnetaan janan $FE$ pituus, koska se on kartion korkeus $6$. Jotta kulma $\alpha$ saadaan ratkaistuksi, tarvitaan joko sivun $AE$ tai $AF$ pituus. Kumpikin selviää Pythagoraan lauseella. Selvitetään nyt esimerkiksi sivun $AF$ pituus. Pohjaneliön lävistäjän $AC$ pituus on $\sqrt{8^2+8^2}=\sqrt{128}=8\sqrt{2}$. $AF$ on puolet lävistäjästä, eli $|AF|=\frac{1}{2}\cdot 8\sqrt{2}=4\sqrt{2}$. (1 p.)
Nyt kulma $\alpha$ saadaan yhtälöstä
$\tan \alpha = \frac{6}{4\sqrt{2}}$, josta $\alpha=46{,}68\ldots^{\circ}\approx 47^{\circ}$. (1 p.)
Pallon sisään asetetaan suurin mahdollinen kuutio. Kuution ylätahkon kärkien kautta piirretään taso, joka rajoittaa pallosta yläosasta pallosegmentin. Kuinka monta prosenttia pallosegmentin korkeus on pallon säteestä?
Vihje: Anna pallon säteeksi jokin luku, jos kirjaimella työskentely tuntuu hankalalta. Yritä lopuksi tehdä tehtävä kirjaimenkin avulla.
Hahmotellaan kuva.
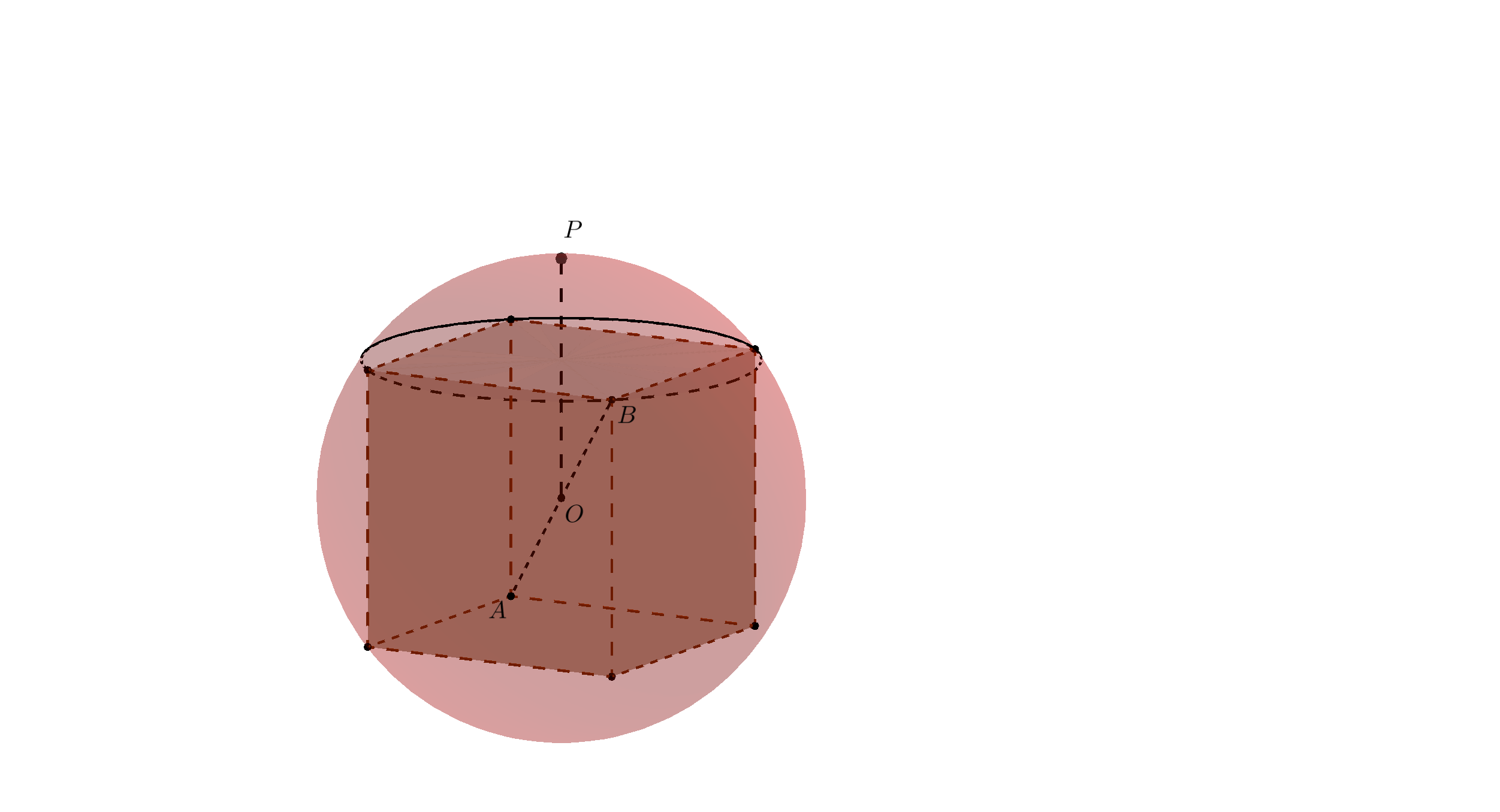
Kuvaan on merkitty kuution avaruuslävistäjä $AB$, pallon keskipiste $O$ ja pallon pystysuora säde $OP$. Ratkaisevaa tehtävässä on, että onnistuu päättelemään, että kuution avaruuslävistäjä on pallon halkaisija. (1 p.) Poikkileikataan pallo kuution pohjatahkoa vastaan kohtisuoralla tasolla, joka kulkee pisteiden $A$ ja $B$ kautta, eli että taso sisältää avaruuslävistäjän $AB$. Piirretään poikkileikkauksesta kuva.
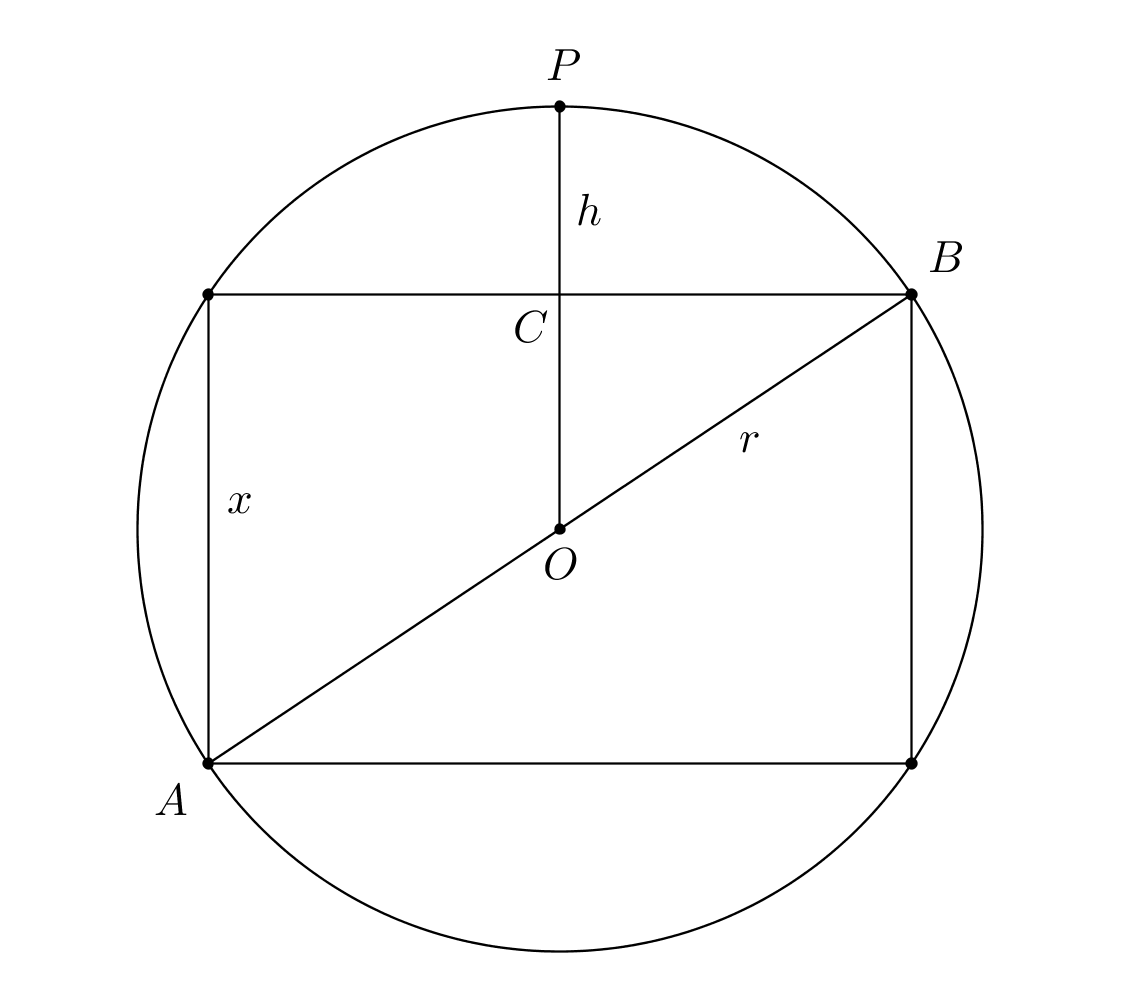 Kuva (1 p.)
Kuva (1 p.)
Jotta voidaan laskea, kuinka monta prosenttia pallosegmentin korkeus on pallon säteestä, täytyy pallosegmentin korkeus $h$ saada lausuttua pallon säteen $r$ avulla.
Lausutaan ensin kuution särmän pituus $x$ pallon säteen avulla. Koska kuution avaruuslävistäjä on pallon halkaisija, saadaan
$d^2=x^2+x^2+x^2=3x^2=(2r)^2$, josta $x^2=\frac{4r^2}{3}$, josta $x=\frac{2r}{\sqrt{3}}$. (1 p.)
Poikkileikkauskuvassa $h=|OP|-|OC|$, missä $|OP|=r$ ja $|OC|=\frac{1}{2}x=\frac{1}{2}\cdot \frac{2r}{\sqrt{3}}=\frac{r}{\sqrt{3}}$. (1 p.)
Sijoittamalla nämä saadaan $h=r-\frac{r}{\sqrt{3}}=\frac{\sqrt{3}r-r}{\sqrt{3}}=\frac{r(\sqrt{3}-1)}{\sqrt{3}}$. (1 p.)
Edellä saatiin $h=\frac{r(\sqrt{3}-1)}{\sqrt{3}}=r\cdot 0{,}422\ldots =0{,}422\ldots r\approx 0{,}42r$. Pallosegmentin korkeus on siis $42$ % pallon säteestä. (1 p.)
Vastaus: Pallosegmentin korkeus on $42$ % pallon säteestä.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
