Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA5-kurssin itsearviointiin.
a) Esittääkö yhtälö $x^2+y^2-2x+8y+4=0$ ympyrää? Myönteisessä tapauksessa määritä ympyrän keskipiste ja säde.
b) Laske pisteen $(4,3)$ etäisyys ympyrästä $(x+1)^2+(y-2)^2=4$ yhden desimaalin tarkkuudella. Piirrä kuva.
a) Muokataan yhtälö keskipistemuotoon. Saadaan
\(\begin{align*} x^2+y^2-2x+8y+4&=0 \qquad \, \, \, \, ||\,-4\\ x^2-2\cdot x\cdot 1+y^2+2\cdot y\cdot 4&=-4 \qquad || \, +1^2+4^2\\ \left(x^2-2\cdot x\cdot 1+1^2\right) +\left( y^2+2\cdot y\cdot 4+4^2\right)&=-4+1^2+4^2\\ (x-1)^2+(y+4)^2&=13. \end{align*}\)
(Yhtälön vasen puoli oikein (1 p.), yhtälön oikea puoli oikein (1 p.))
Koska yhtälön oikea puoli on positiivinen, niin yhtälö esittää ympyrää ja sen keskipiste on $(1,-4)$ ja säde on $\sqrt{13}$. (1 p.)
b) Koska ympyrän yhtälö on $(x+1)^2+(y-2)^2=4$, niin sen keskipiste on $(-1,2)$ ja säde $r=\sqrt{4}=2$. Piirretään kuva.
 (1 p.)
(1 p.)
Kysytty etäisyys on janan $BP$ pituus. Koska pistettä $P$ ei tunneta, niin selvitetään janan pituus ympyrän keskipisteen avulla. Lasketaan aluksi janan $AB$ pituus, eli pisteen $B$ etäisyys ympyrän keskipisteestä $A$ ja vähennetään tästä ympyrän säde, eli janan $AP$ pituus. (Idea janan etäisyyden laskemiseksi (1 p.))
Saadaan $$|AB|=\sqrt{(4-(-1))^2+(3-2)^2}=\sqrt{25+1}=\sqrt{26}.$$
Kysytty etäisyys on $$|BP|=|AB|-r=\sqrt{26}-2=3{,}0990\ldots\approx 3{,}1.$$ (1 p.)
a) Määritä ympyröiden $x^2+y^2-9=0$ ja $(x-2)^2+y^2=1$ leikkauspisteet.
b) Tehtävänä on pohtia, miten kaksi eri ympyrää voivat sijaita suhteessa toisiinsa ja miten ympyröiden keskipisteiden etäisyys vaikuttaa leikkauspisteiden lukumäärään. Tarkastellaan a)-kohdan ympyrää $x^2+y^2-9=0$ sekä 1-säteistä ympyrää. Piirrä erilaisia tilanteita, miten 1-säteinen ympyrä voi sijaita suhteessa isompaan ympyrään leikkauspisteiden lukumäärän kannalta. Millainen ehto tehtävän ympyröiden keskipisteiden etäisyyden tulee täyttää, jotta
- leikkauspisteitä ei ole
- leikkauspisteitä on yksi
- leikkauspisteitä on kaksi?
a) Muokataan ympyrän yhtälöt yleiseen muotoon. Saadaan yhtälöpari
\(\begin{cases} x^2+y^2-9&=0\\ x^2+y^2-4x+3&=0. \end{cases}\)
Kerrotaan esimerkiksi alempaa yhtälöä luvulla $-1$, jolloin saadaan yhtälöpari
\(\begin{cases} x^2+y^2-9&=0\\ -x^2-y^2+4x-3&=0. \end{cases}\)
Lasketaan yhtälöt allekkain yhteen, jolloin saadaan yhtälö $4x-12=0$, jonka ratkaisu on $x=3$. (Idea yhtälöparin ratkaisusta (1 p.), $x=3$ (1 p.)) Ympyröiden leikkauspisteen $x$-koordinaatti on siis $3$. Leikkauspisteen $y$-koordinaatti saadaan, kun sijoitetaan $x=3$ jompaankumpaan alkuperäisistä yhtälöistä. Saadaan $3^2+y^2-9=0$, eli $y^2=0$, josta $y=0$. (1 p.)
Vastaus: Ympyrät leikkaavat pisteessä $(3,0)$.
b) Jos ympyröillä ei ole leikkauspisteitä, voi tilanne olla jompikumpi (vihreä tai punainen) seuraavista:
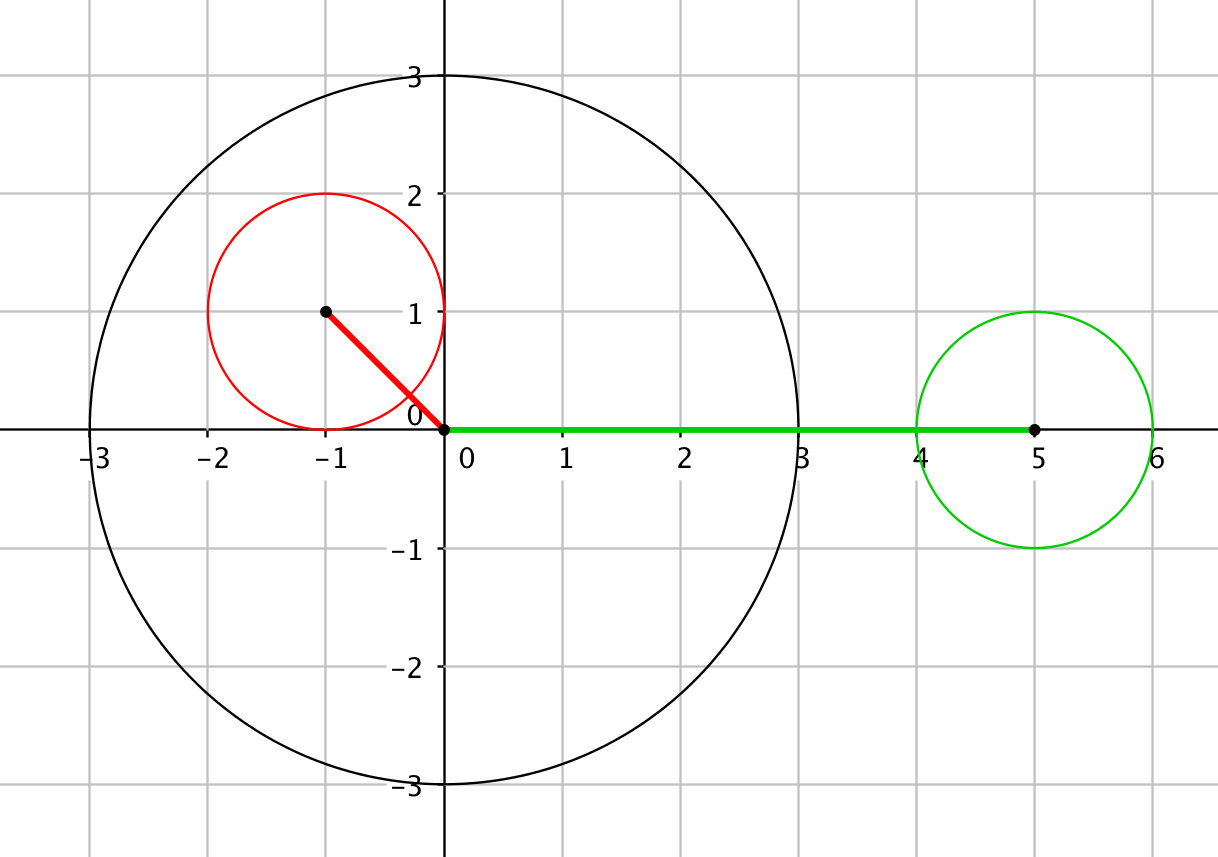
Vihreässä tilanteessa ympyröiden keskipisteiden välinen etäisyys on suurempi kuin säteiden summa $4$. Punaisessa tilanteessa ympyröiden keskipisteiden välinen etäisyys on pienempi kuin ympyröiden säteiden erotus $2$.
Jos ympyröillä on tasan yksi leikkauspiste, voi tilanne jolla jompikumpi (vihreä tai punainen) seuraavista:
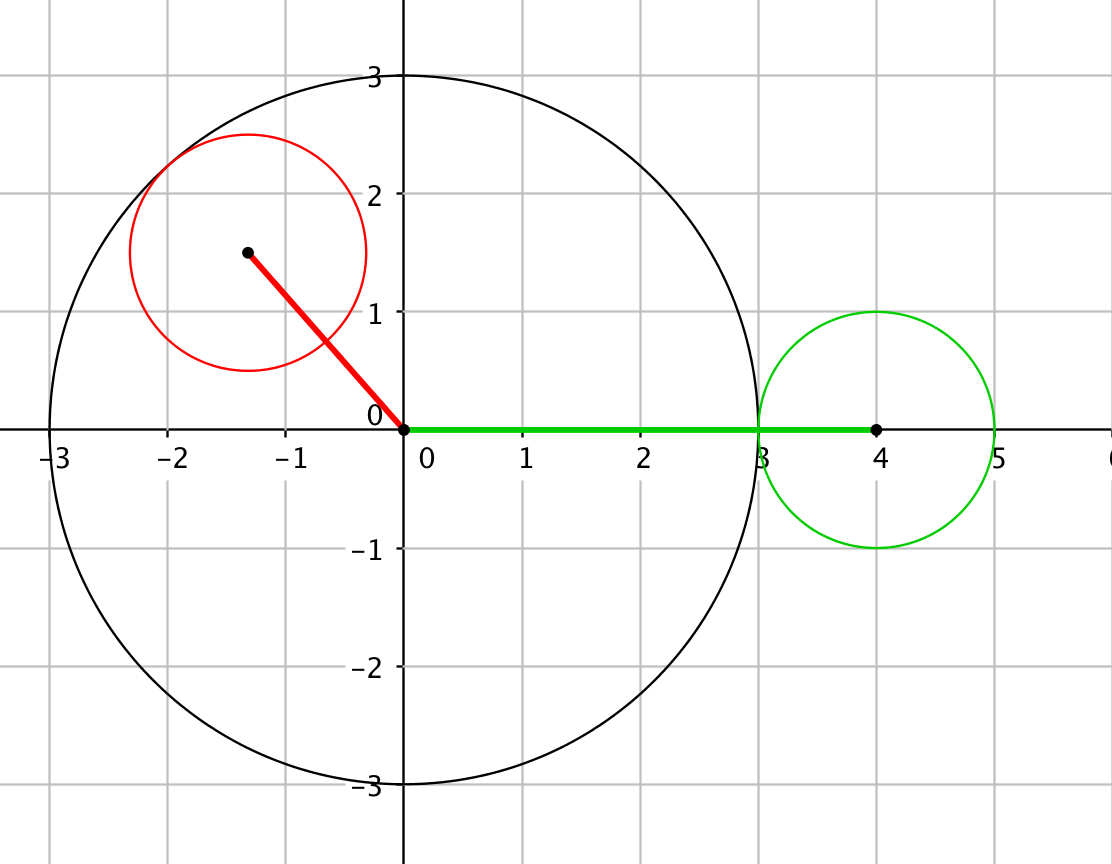
Vihreässä tilanteessa ympyröiden keskipisteiden välinen etäisyys on täsmälleen ympyröiden säteiden summa $4$. Punaisessa tilanteessa ympyröiden keskipisteiden välinen etäisyys on täsmälleen säteiden erotus $2$.
Jos ympyröillä on kaksi leikkauspistettä, voi tilanne olla seuraava:
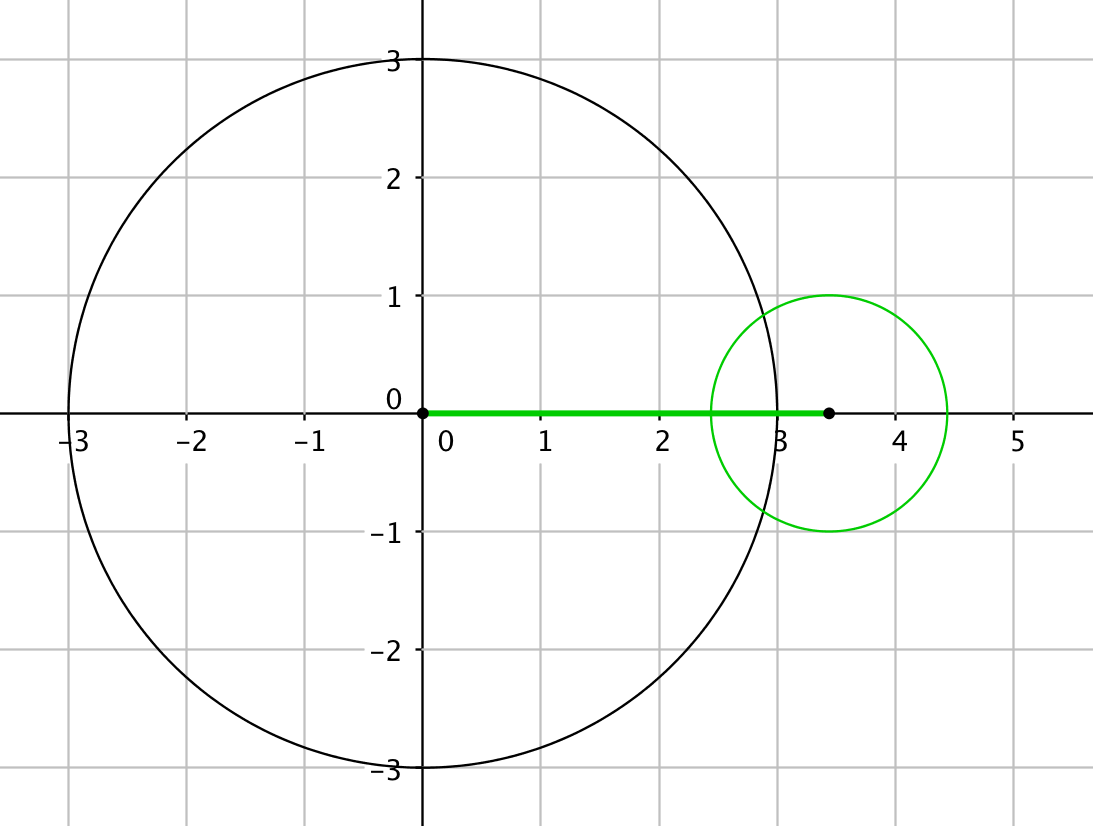
Nyt tilanteita on enää yksi. Ympyröiden keskipisteiden välinen etäisyys tulee olla edellisen kohdan etäisyyksien välissä, eli etäisyyden $d$ tulee olla $2<d<4$. Toisin sanoen etäisyyden pitää olla suurempi kuin säteiden erotus, jotta ympyrä ei enää sivua ympyrää. Toisaalta etäisyys ei voi olla suurempi kuin säteiden summa, koska muuten ympyrät eivät lainkaan leikkaisi.
(Kolme erilaista kuvaa (1 p.), kolme ehtoa ympyröiden keskipisteiden väliselle etäisyydelle (1 p.), kaikki viisi tilannetta oikein perusteluineen (1 p.))
Muodosta yhtälöt ympyrän $x^2-6x+y^2-2y+1=0$ tangenteille, jotka kulkevat pisteen $(-3,4)$ kautta.
Määritetään aluksi ympyrän keskipiste ja säde kuvan piirtämistä varten.
\(\begin{align*} x^2-6x+y^2-2y+1&=0\\ x^2-2\cdot x\cdot 3+(y-1)^2&=0\\ x^2-2\cdot x \cdot 3 +3^2+(y-1)^2&=3^2\\ (x-3)^2+(y-1)^2&=3^2, \end{align*}\)
joten ympyrän keskipiste on $(3,1)$ ja säde $r=3$. Piirretään tilanteesta kuva.
 (1 p.)
(1 p.)
Kuvan perusteella näyttää, että tangentteja voisi piirtää ympyrälle kaksi. Näytetään vielä tämä, eli lasketaan pisteen $(-3,4)$ etäisyys ympyrän keskipisteestä ja osoitetaan, että se on suurempi kuin säde $3$. Saadaan $d=\sqrt{(-3-3)^2+(4-1)^2}=\sqrt{36+9}=\sqrt{45}=3\sqrt{5}>3$. (1 p.)
Muodostetaan tangentille aluksi normaalimuotoinen yhtälö. Tangentti kulkee pisteen $(-3,4)$ kautta, mutta kulmakerrointa $k$ ei tunneta. Näin ollen yhtälöksi saadaan
\(\begin{align*} y-4&=k(x-(-3))\\ y-4&=kx+3k\\ kx-y+(3k+4)&=0. \end{align*}\)
(1 p.)
Tangentin etäisyys ympyrän keskipisteestä on ympyrän säde $3$, koska tangentti aina sivuaa ympyrää. Muodostetaan tiedosta yhtälö pisteen etäisyys suorasta -kaavan avulla. Nyt suoran normaalimuotoisessa yhtälössä $ax+by+c=0$ on $a=k, b=-1$ ja $c=3k+4$ ja $(x_0,y_0)=(3,1)$. Saadaan
\(\begin{align*} \dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}&=r\\ \dfrac{|k\cdot 3-1\cdot 1+(3k+4)|}{\sqrt{k^2+(-1)^2}}&=3\\ \dfrac{|6k+3|}{\sqrt{k^2+1}}&=3 \\ |6k+3|&=3\sqrt{k^2+1} \qquad || \text{ Korotetaan molemmat puolet toiseen.}\\ |6k+3|^2&=(3\sqrt{k^2+1})^2 \\ (6k+3)^2&=9(k^2+1)\\ 36k^2+36k+9&=9k^2+9\\ 27k^2+36k&=0\\ 9k(3k+4)&=0\\ 9k&=0 \text{ tai } 3k+4=0\\ k&=0 \text{ tai } k=-\frac{4}{3}. \end{align*}\)
(Sijoitus kaavaan (1 p.), kulmakertoimet oikein (1 p.))
Kysytyt tangenttien yhtälöt siis ovat $0x-y+(3\cdot 0+4)=0$ eli $y=4$ ja $-\frac{4}{3}x-y+\left(3\cdot \left( -\frac{4}{3}\right)+4\right)=0$, josta saadaan $-\frac{4}{3}x-y=0$, eli $y=-\frac{4}{3}x$. Kuvan perusteella yhtälöt näyttävät järkeviltä.
Vastaus: Tangenttien yhtälöt ovat $y=4$ ja $y=-\frac{4}{3}x$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
