Testi on tarkoitettu kisallioppiminen.fi -sivuton MAA6-kurssin itsearviointiin.
Vastaa kuvan avulla seuraaviin kysymyksiin.
a) Määritä $f(0)$. (1 p.)
b) Määritä $f'(0)$. (1 p.)
c) Onko $f'(2)$ positiivinen vai negatiivinen? Perustele. (2 p.)
d) Määritä kohdat, joissa $f'(x)=0$. Perustele. (2 p.)
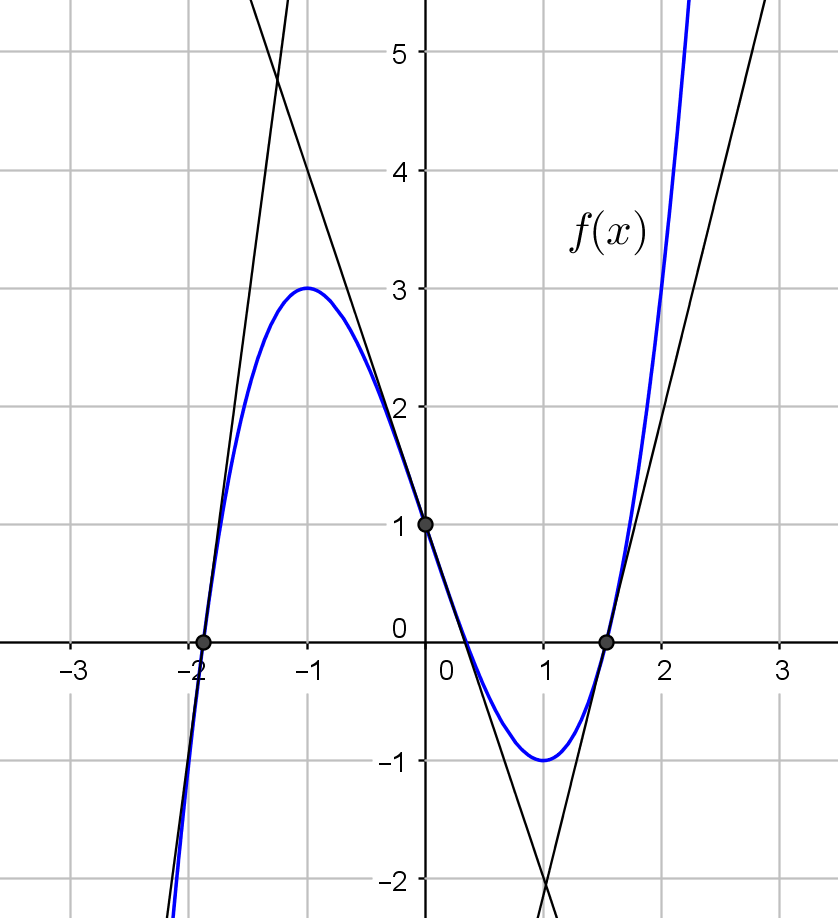
a) $f(0)=1$ (1 p.) eli funktion arvo kohdassa $x=0$ on $1$.
b) $f'(0)=-3$ (1 p.) eli kuvaajalle kohtaan $x=0$ piirretyn tangentin kulmakerroin on $-3$.
c) $f'(2)>0$ (1 p.) koska jos kuvaajalle piirretään tangentti kohtaan $x=2$, on se nouseva, eli kulmakerroin on positiivinen. (1 p.)
d) $f'(x)=0$, kun $x=-1$ tai $x=1$. (1 p.) Kyseisiin kohtiin kuvaajalle piirretyt tangentit ovat vaakasuoria, eli niiden kulmakerroin on nolla. (1 p.)
a) Tarkastellaan funktiota $f(x)$ välillä $[-1,3]$. Tutki oheista Geogebra-sovellusta ja vastaa sen avulla seuraaviin kysymyksiin.
i) Määritä $f'(-0{,}5)$. (1 p.)
ii) Milloin $f'(x)<0$? (1 p.)
iii) Missä kohdassa $x, -1\leq x\leq 3$, funktio $f(x)$ kasvaa kaikkein voimakkaimmin? (1 p.)
b) Funktiosta $f(x)$ tiedetään, että $f(0)=4 $ ja $f'(x)=2$ kaikilla $x$. Piirrä derivaattafunktion $f'(x)$ ja funktion $f(x) $ kuvaajat. (3 p.)
a)
i) $f'(-0{,}5)=0{,}75$ (1 p.)
ii) $f'(x)<0$, kun $0<x<2$. (1 p.)
iii) Funktio $f(x)$ kasvaa voimakkaimmin kohdissa $x=3$ ja $x=-1$, koska derivaatan arvo on siinä suurin ($f'(3)=f'(-2)=1{,}8$). (1 p.)
b) Koska $f'(x)=2$ kaikissa kohdissa $x$, niin kyseessä on vakiofunktio ja sen kuvaaja on vaakasuora korkeudella $2$. Toisaalta derivaattafunktion arvot kertovat funktion kasvunopeuden, joten funktion $f(x)$ kuvaajalle jokaiseen kohtaan $x$ piirretyn tangentin kulmakerroin on aina kaksi. Näin ollen alkuperäinen funktio on ensimmäisen asteen polynomi, jonka kulmakerroin on kaksi. Lisäksi se leikkaa $y$-akselin pisteessä $(0,4)$.
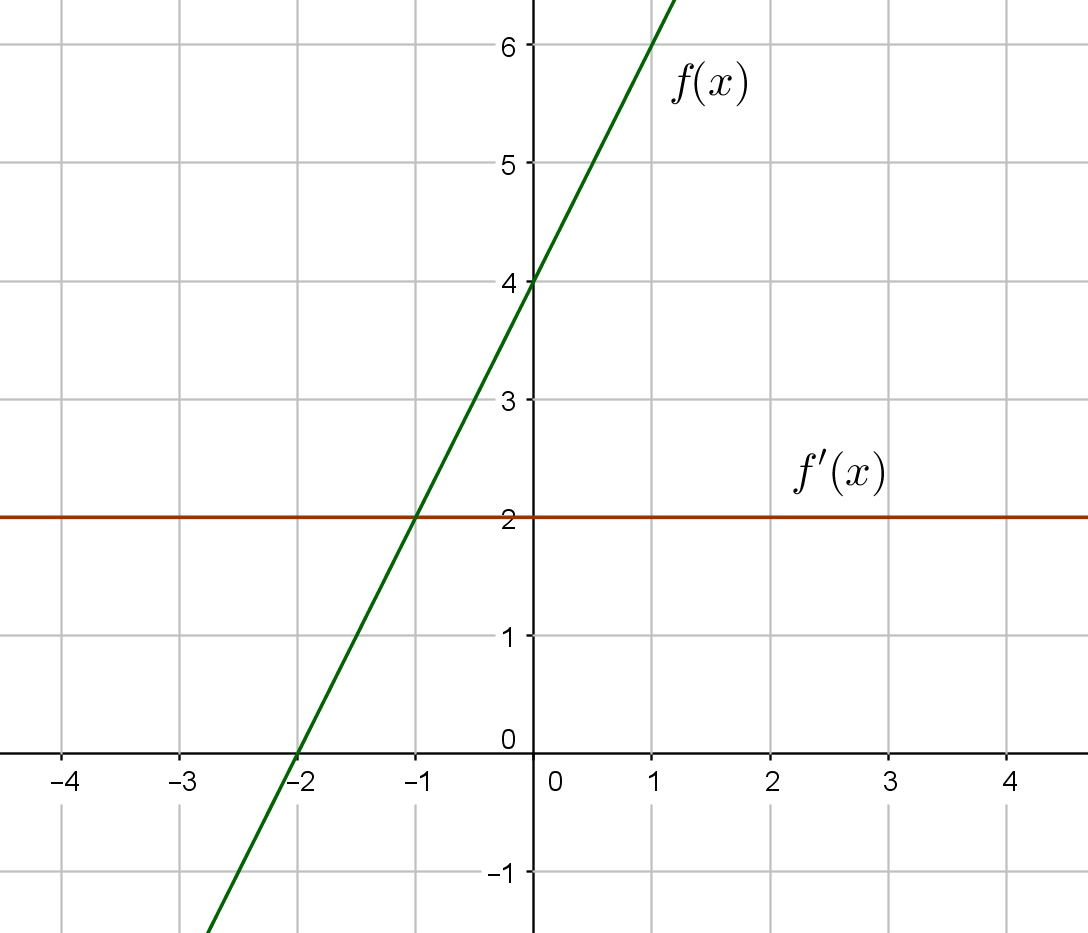
Derivaattafunktion kuvaaja oikein (1 p.)
Funktion kuvaaja kulkee pisteen $(0,4)$ kautta (1 p.)
Funktion kuvaaja oikein (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
