Testi on tarkoitettu kisallioppiminen.fi -sivun MAA6-kurssin itsearviointiin.
Ohessa on funktion $f(x)$ kuvaaja. Vastaa sen avulla seuraaviin kysymyksiin. Perustele sanallisesti.
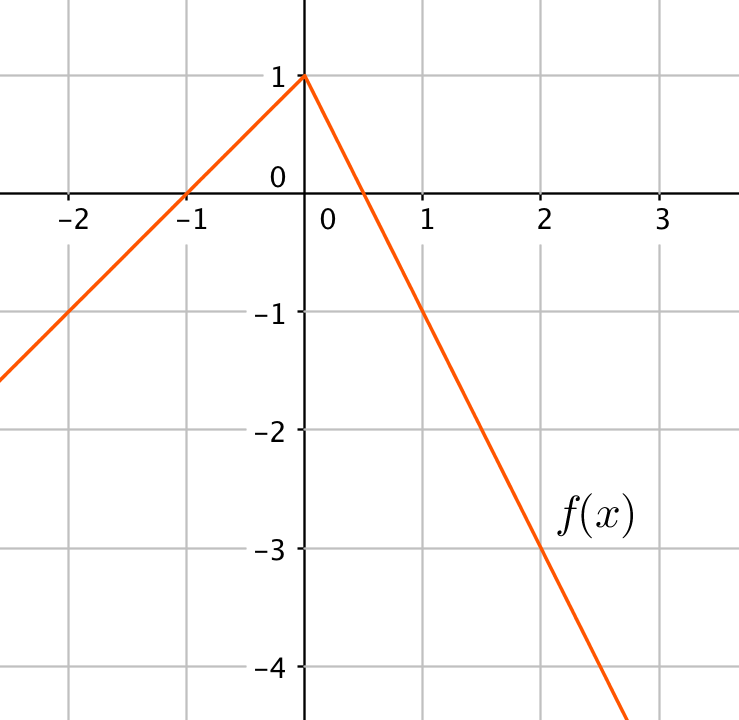
a) Onko funktiolla raja-arvo kohdassa $x=0$?
b) Onko funktio jatkuva kohdassa $x=0$?
c) Onko funktio derivoituva kohdassa $x=0$?
a) Funktiolla on raja-arvo kohdassa $x=0$ (1 p.), koska lähestyttäessä kohtaa $x=0$ sekä vasemmalta että oikealta funktio arvot menevät kohti lukua $1$. (1 p.)
b) Funktio on jatkuva kohdassa $x=0$ (1 p.), koska funktion arvo nollassa on sama kuin funktion raja-arvo nollassa, eli $\lim_{x\rightarrow0}f(x)=f(0)=1$. (1 p.)
c) Funktio ei ole derivoituva kohdassa $x=0$ (1 p.), koska lähestyttäessä vasemmalta kohtaa $x=0$ tangentin kulmakertoimet ovat $1$ ja oikealta lähestyttäessä tangentin kulmakertoimet ovat $-2$. (1 p.) Toinen tapa perustella on näyttää, että kohtaan $x=0$ ei voi piirtää yksikäsitteistä tangenttia.
Tutki laskemalla, onko funktiolla
\(f(x)=\begin{cases} x^2+3x, x<-1\\ 2x-2, x\geq-1 \end{cases}\)raja-arvo kohdassa $x=-1$. Myönteisessä tapauksessa määritä se.
Koska funktio on paloittain määritelty kohdan $x=-1$ ympäristössä, tulee tutkia toispuolisia raja-arvoja kohdassa $x=-1$. (1 p.)
Vasemmanpuoleinen raja-arvo on
$$\lim_{x\rightarrow (-1)-}f(x)=\lim_{x\rightarrow (-1)-} (x^2+3x)=(-1)^2+3\cdot (-1)=1-3=-2.$$ (Sijoitus oikeaan lausekkeeseen (1 p.) ja arvo oikein (1 p.))
OIkeanpuoleinen raja-arvo on
$$f(x)=2x-2\rightarrow2\cdot (-1)-2=-4, \text{ kun } x\rightarrow (-1)+.$$ (Sijoitus oikeaan lausekkeeseen ja arvo oikein (1 p.))
Koska vasemman- ja oikeanpuoleiset raja-arvot eivät olleet yhtä suuret, eli $\lim_{x\rightarrow (-1)-}f(x)=-2\neq-4= \lim_{x\rightarrow (-1)+}$, niin funktiolla ei ole raja-arvoa kohdassa $x=-1$. (1 p.)
(Merkinnät oikein raja-arvolaskuissa, eli joko $\lim_{x\rightarrow (-1)-} f(x)$, tai nuoli $\rightarrow$ ja loppuun merkintä $x\rightarrow (-1)-$ (1 p.))
Osoita, että funktiolla $f(x)=x^5-4x+1$ on ainakin yksi nollakohta.
Funktio $f(x)=x^5-4x+1$ on polynomifunktiona jatkuva. (1 p.) Tutkitaan aluksi funktion kuvaajaa.
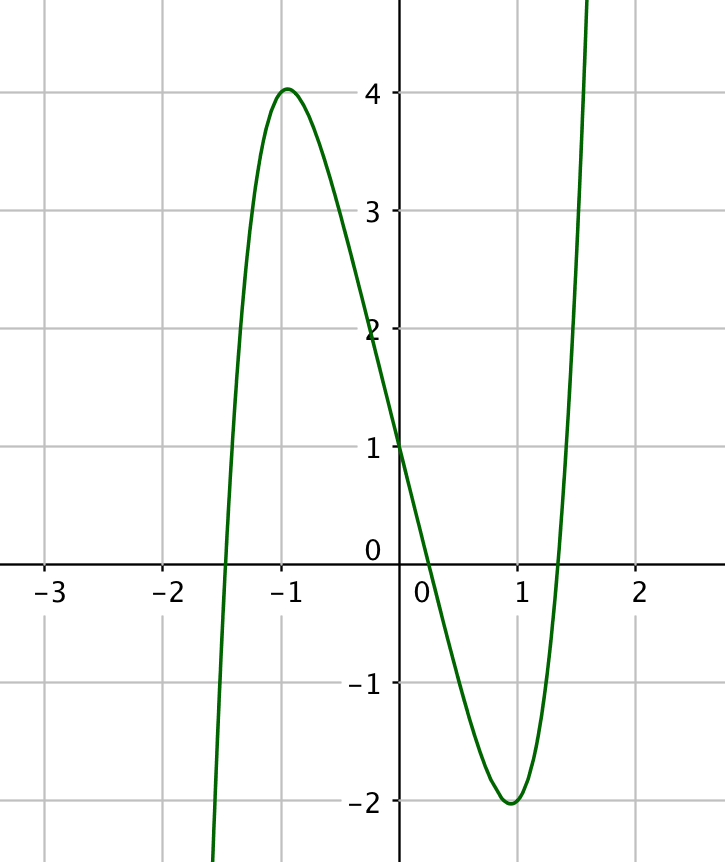
Huomataan, että esimerkiksi välillä $[0,1]$ näyttäisi olevan yksi nollakohta. (Joku järkevä väli valittu (1 p.))
Lasketaan funktion arvot välin päätepisteissä. Saadaan $f(0)=0^5-4\cdot 0+1=1$ ja $f(1)=1^5-4\cdot 1+1=-2$. (2 p.)
Koska funktion arvot välin päätepisteissä ovat eri merkkiset, niin Bolzanon lauseen nojalla funktiolla on ainakin yksi nollakohta välillä $]0,1[$. (2 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
