Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA6-kurssin itsearviointiin.
Millä muuttujan $x$ arvoilla funktio $f(x)=x^4-x^3+2$ on aidosti kasvava?
Funktion $f(x)$ derivaatta on $f'(x)=4x^3-3x^2$. (1 p.)
Lasketaan derivaatan nollakohdat. Saadaan
\(\begin{align*} 4x^3-3x^2&=0\\ x^2(4x-3)&=0\\ x&=0 \text{ tai }x=\dfrac{3}{4} \end{align*}\)(2 p.)
Laaditaan derivaatan merkkikaavio ja täydennetään se funktion kulkukaavioksi.
Määritetään derivaatan merkit testipisteiden avulla.
$f'(-1)=-7<0$
$f'(\frac{1}{2})=-\dfrac{1}{4}<0$
$f'(2)=20>0$. (1 p.)
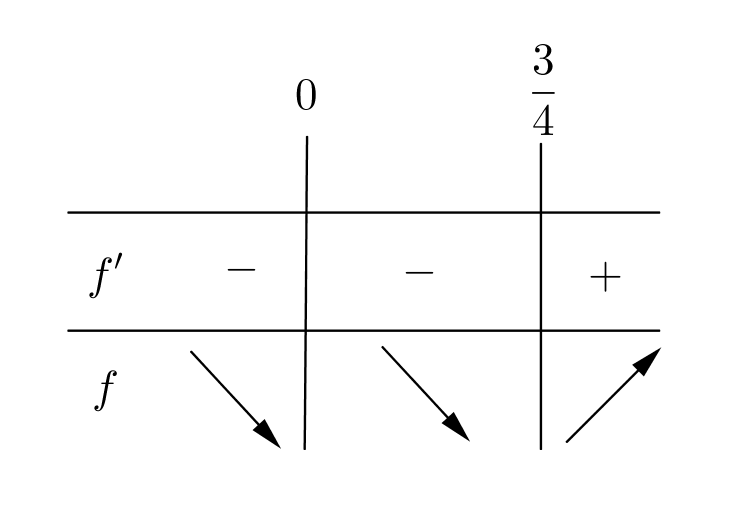(1 p.)
Kulkukaavion perusteella funktio on aidosti kasvava, kun $x\geq \dfrac{3}{4}$. (1 p.)
Ohessa on funktion $f(x)$ derivaattafunktion $f'(x)$ kuvaaja. Vastaa sen avulla oheisiin kysymyksiin.
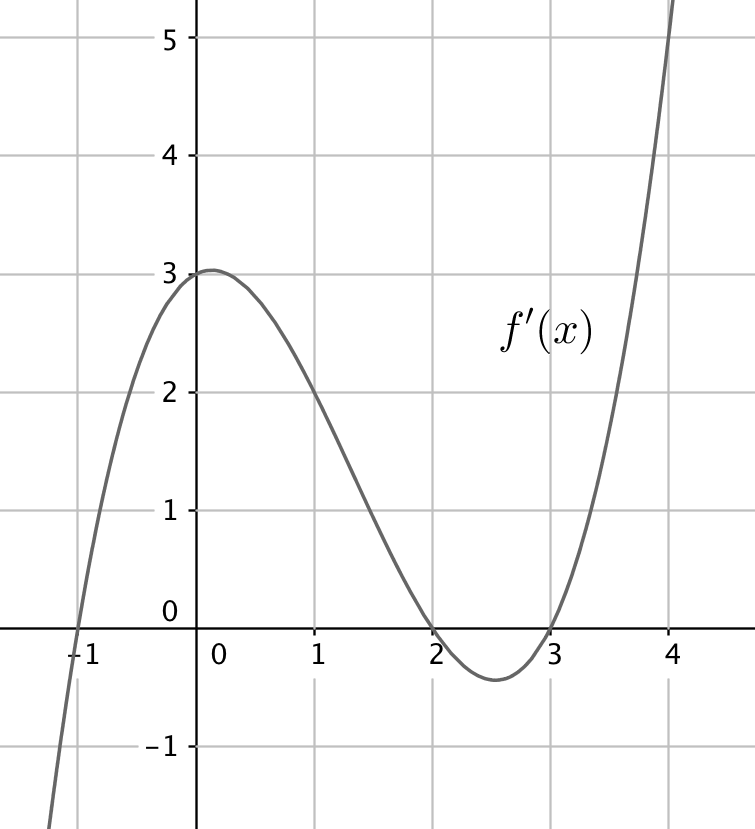
a) Millä muuttujan $x$ arvoilla $f(x)$ on vähenevä?
b) Määritä funktion $f(x)$ ääriarvokohdat.
c) Tiedetään, että $f(-1)>0$. Mitä tiedät funktion $f(x)$ nollakohtien enimmäismäärästä?
a) Funktio on vähenevä, kun $f'(x)\leq 0$ (1 p.), eli kun $x\leq -1$ tai $2\leq x\leq 3$. (1 p.)
b) Laaditaan derivaatan merkkikaavio ja laajennetaan se funktion kulkukaavioksi derivaattafunktion kuvaaajan perusteella.
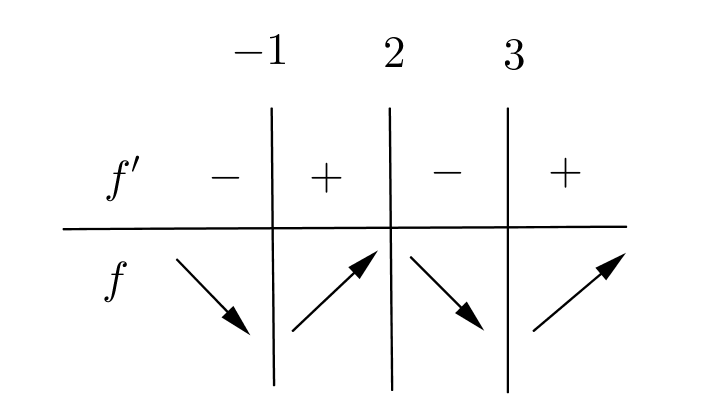
Kulkukaavion perusteella funktiolla on minimikohdat $x=-1$ ja $x=3$ (1 p.) sekä maksimikohta $x=2$. (1 p.)
c) Koska $f(-1)>0$, niin $f(x)>0$ kaikilla $x$, $x\leq 2$. (1 p.)
Näin ollen välillä $]2,3]$ voi olla korkeintaan yksi nollakohta ja välillä $]3,\infty[$ korkeintaan yksi nollakohta, koska ko. väleillä funktio on jatkuva ja aidosti monotoninen. (1 p.)
HUOM. Jos lisäksi oltaisiin tiedetty, että $f(3)>0$, niin kulkukaavion perusteella oltaisiin tiedetty, että funktiolla ei ole yhtään nollakohtaa. Jos $f(3)=0$, niin nollakohtia olisi tasan yksi ja jos $f(3)<0$, niin nollakohtia olisi tasan kaksi.
Suorakulmion kärjistä yksi on origossa, yksi pisteessä $(x,0)$, $0\leq x\leq 9$, ja yksi käyrällä $y=9x-x^2$. Määritä suorakulmion suurin mahdollinen pinta-ala.
Hahmotellaan tilanteesta kuva.
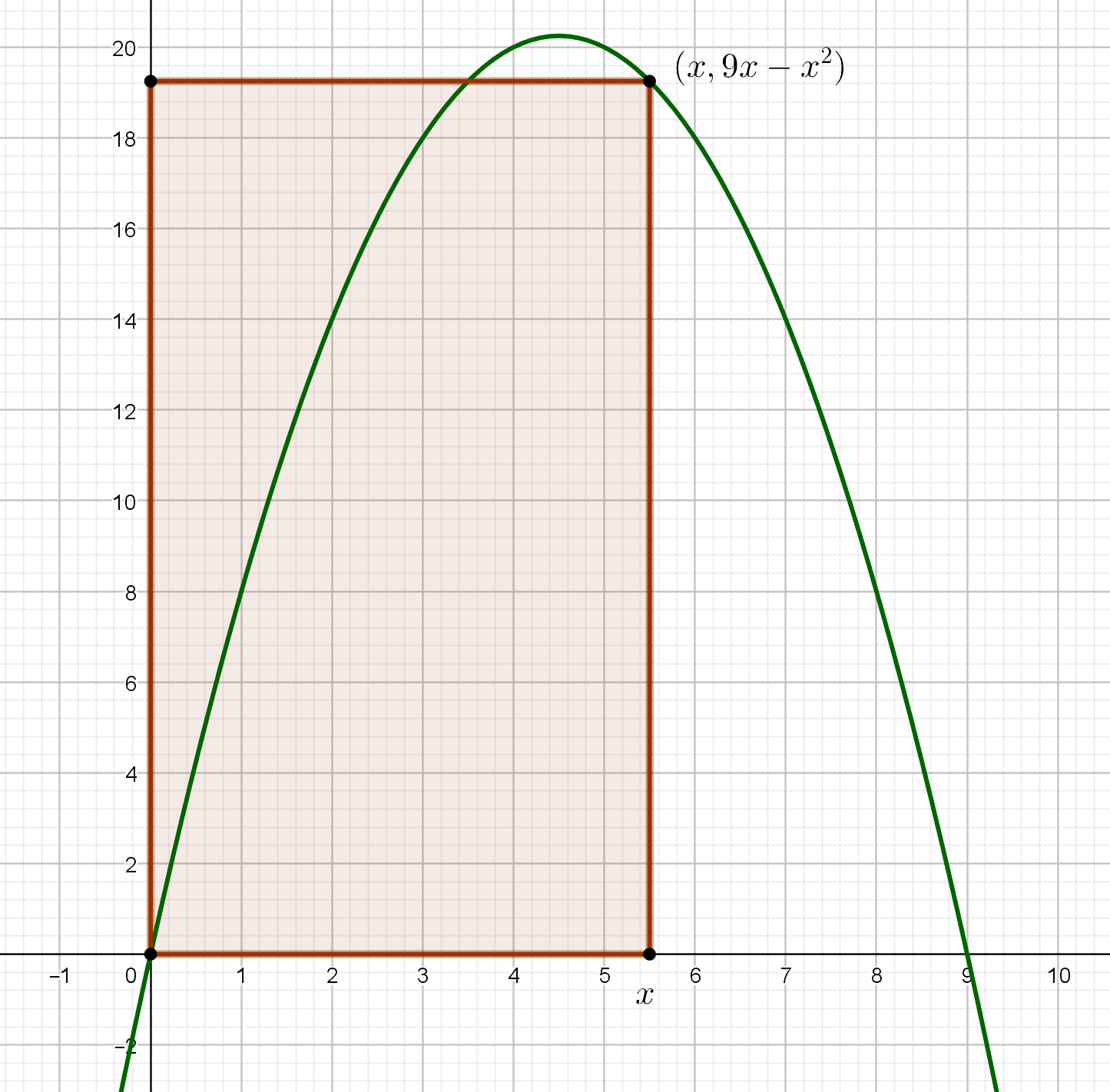
(1 p.)
Suorakulmion kanta on siis $x$ ja korkeus $9x-x^2$. (1 p.)
Näin ollen suorakulmion pinta-ala on $A(x)=x(9x-x^2)=9x^2-x^3$. (1 p.)
Pinta-alafunktio on jatkuva suljetulla välillä $[0,9]$ ja derivoituva vastaavalla avoimella välillä $]0,9[$, joten se suurimman arvonsa välin päätepisteissä tai niissä derivaatan nollakohdissa, jotka kuuluvat välille $]0,9[$. (1 p.)
Derivoidaan $A(x)$ ja lasketaan derivaatan nollakohdat.
$A'(x)=9\cdot 2x-3x^2=18x-3x^2$, jonka nollakohdat saadaan yhtälöstä $18x-3x^2=0$.
\(\begin{align*} 18x-3x^2&=0\\ 3x(6-x)&=0\\ x&=0 \text{ tai } x=6. \end{align*}\)
Lasketaan pinta-alan arvo kohdissa $x=0, x=6$ ja $x=9$.
$A(0)=9\cdot 0^2-0^3=0$
$A(6)=9\cdot 6^2-6^3=108$
$A(9)=9\cdot 9^2-9^3=0$. (1 p.)
Pinta-alan suurin arvo on siis $108$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: