Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA7-kurssin itsearviointiin.
a) Muuta seuraavat asteet radiaaneiksi: $90^{\circ}, 30^{\circ}$ ja $156^{\circ}$. (2 p.)
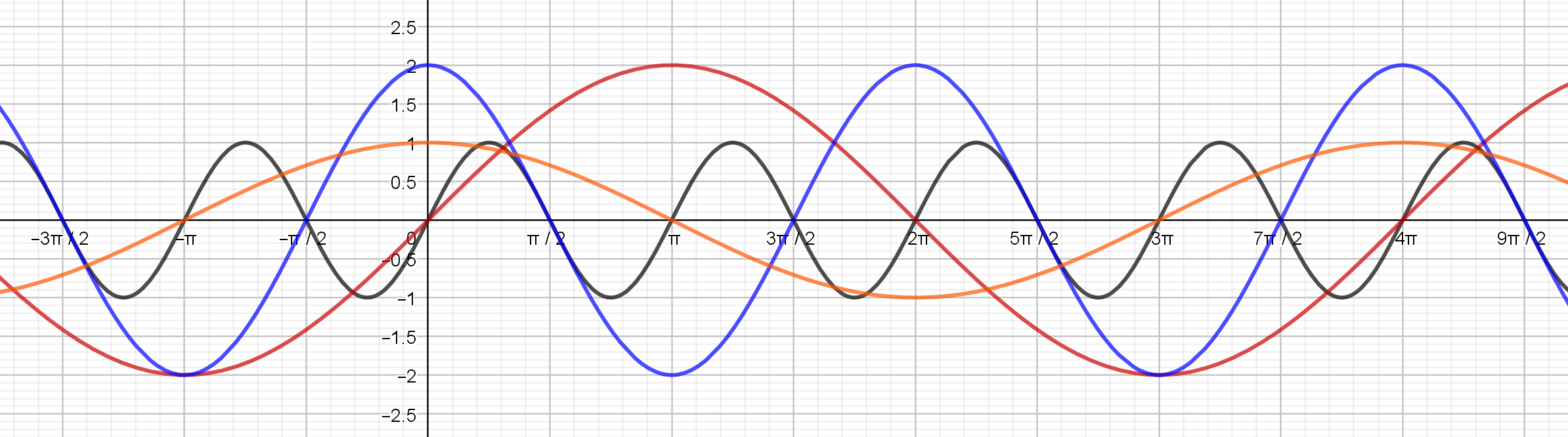
b) Yhdistä oikea funktion lauseke oikeaan kuvaajaan. Osa lausekkeista jää käyttämättä. (4 p.)
- $\sin (2x)$
- $\sin \left(\frac{1}{2}x\right)$
- $2\sin x$
- $2\sin \left(\frac{1}{2}x\right)$
- $\cos (2x)$
- $\cos \left(\frac{1}{2}x\right)$
- $2\cos x$
- $2\cos \left(\frac{1}{2}x\right)$
a) Koska $180^{\circ}=\pi$ radiaania, niin $90^{\circ}=\dfrac{\pi}{2}$ radiaania. Samaan tapaan $30^{\circ}=\dfrac{\pi}{6}$ radiaania ja $156^{\circ}=156\cdot \dfrac{\pi}{180}=\dfrac{13\pi}{15}$ radiaania. (Yksi oikein (1 p.), kaksi muuta oikein (1 p.))
b) Päättelyä voi tehdä monella eri tavalla. Eräs tapa on päätellä alkuun, onko kyseessä sini- vai kosinifunktio. Koska $\sin 0=0$, niin punainen ja musta kuvaaja ovat sinifunktion kuvaaija ja toisaalta sininen ja oranssi ovat kosinifunktion kuvaajia. Koska musta kuvaaja saa arvoja välillä $[-1,1]$, ei sinifunktiolla ole kerrointa edessä. Koska mustan kuvaajan jakson pituus on $\pi$, niin kyseessä on $\sin (2x)$ eli numero 1.
Punaisen kuvaajan arvot ovat välillä $[-2,2]$, joten sinifunktion kerroin on $2$. Koska punaisen kuvaajan jakson pituus on $4\pi$, on oikea vastaus $2\sin \left( \frac{1}{2}x\right)$ eli numero 4.
Samaan tapaan päätellään kosinifunktion kuvaajat, jolloin oranssi kuvaaja on $\cos \left( \frac{1}{2}x\right)$ eli numero 6 ja sininen kuvaaja on $2 \cos x$ eli numero 7.
(1 p. oikeasta vastauksesta, yht. 4 p.)
a) Määritä $\sin \alpha$ tarkka arvo, kun $\cos \alpha=\dfrac{5}{9}$ ja $\dfrac{3\pi}{2}\leq\alpha\leq 2\pi$.
b) Ratkaise yhtälö $\sin 2x+2\cos x=0$ radiaaneina.
a) Koska kosinin arvo $\cos \alpha$ tunnetaan, niin selvitetään sinin arvo yhtälöstä $\sin^2\alpha+\cos^2\alpha=1$. Saadaan
\(\begin{align*} \sin^2\alpha+\left( \dfrac{5}{9}\right)^2&=1\\ \sin^2\alpha+\dfrac{25}{81}&=1\\ \sin^2\alpha&=1-\dfrac{25}{81}\\ \sin^2\alpha&=\dfrac{56}{81}. \end{align*}\)(Yhtälö oikein (1 p.))
Ottamalla neliöjuuri yhtälön molemmilta puolilta saadaan
\(\begin{align*} \sin \alpha=\sqrt{\dfrac{56}{81}}=\dfrac{2\sqrt{14}}{9} \text{ tai } \sin \alpha=-\sqrt{\dfrac{56}{81}}=-\dfrac{2\sqrt{14}}{9}. \end{align*}\)(1 p.)
Koska kulma $\alpha$ sijaitsee neljännessä neljänneksessä ( $\dfrac{3\pi}{2}\leq\alpha\leq 2\pi$), on sinin arvo negatiivinen, joten $\sin \alpha=-\dfrac{2\sqrt{14}}{9}$. (1 p.)
b) Koska yhtälössä $\sin 2x+2\cos x=0$ esiintyy sekä siniä että kosinia ja näiden kulmat ovat eri suuruiset ($2x$ ja $x$), niin yhtälöä pitää muokata. Käytetään tietoa $\sin 2x=2\sin x\cos x$. Tällöin yhtälö saa muodon
\(\begin{align*} &2\sin x\cos x+2\cos x=0, \\ &\text{josta ottamalla yhteinen tekijä } \cos x \text{ saadaan}\\ &\cos x(2\sin x+2)=0. \end{align*}\) (Yhtälö saatu tulomuotoon (1 p.))
Tulon nollasäännön mukaan yhtälö on tosi, kun $\cos x=0$ tai $2\sin x+2=0$. Ratkaistaan nämä yhtälöt. Saadaan
\(\begin{align*} \cos x&=0\\ x&=\pm\dfrac{\pi}{2}+n\cdot 2\pi\\ x&=\dfrac{\pi}{2}+n\cdot \pi. \end{align*}\)
\(\begin{align*} 2\sin x+2&=0\\ 2\sin x&=-2\\ \sin x&=-1\\ x&=\dfrac{3\pi}{2}+n\cdot 2\pi. \end{align*}\)(Jompikumpi yhtälön ratkaisuista oikein (1 p.))
Huom. Sinin tapauksessa toinen ratkaisu olisi $x=\pi-\dfrac{3\pi}{2}=-\dfrac{\pi}{2}$, jolla on sama loppukylki kuin kulmalla $\dfrac{3\pi}{2}$. Tämän takia sitä ei ole kirjoitettu näkyviin, mutta sen voisi hyvin kirjoittaa ja huomata asian siinä kohtaa.
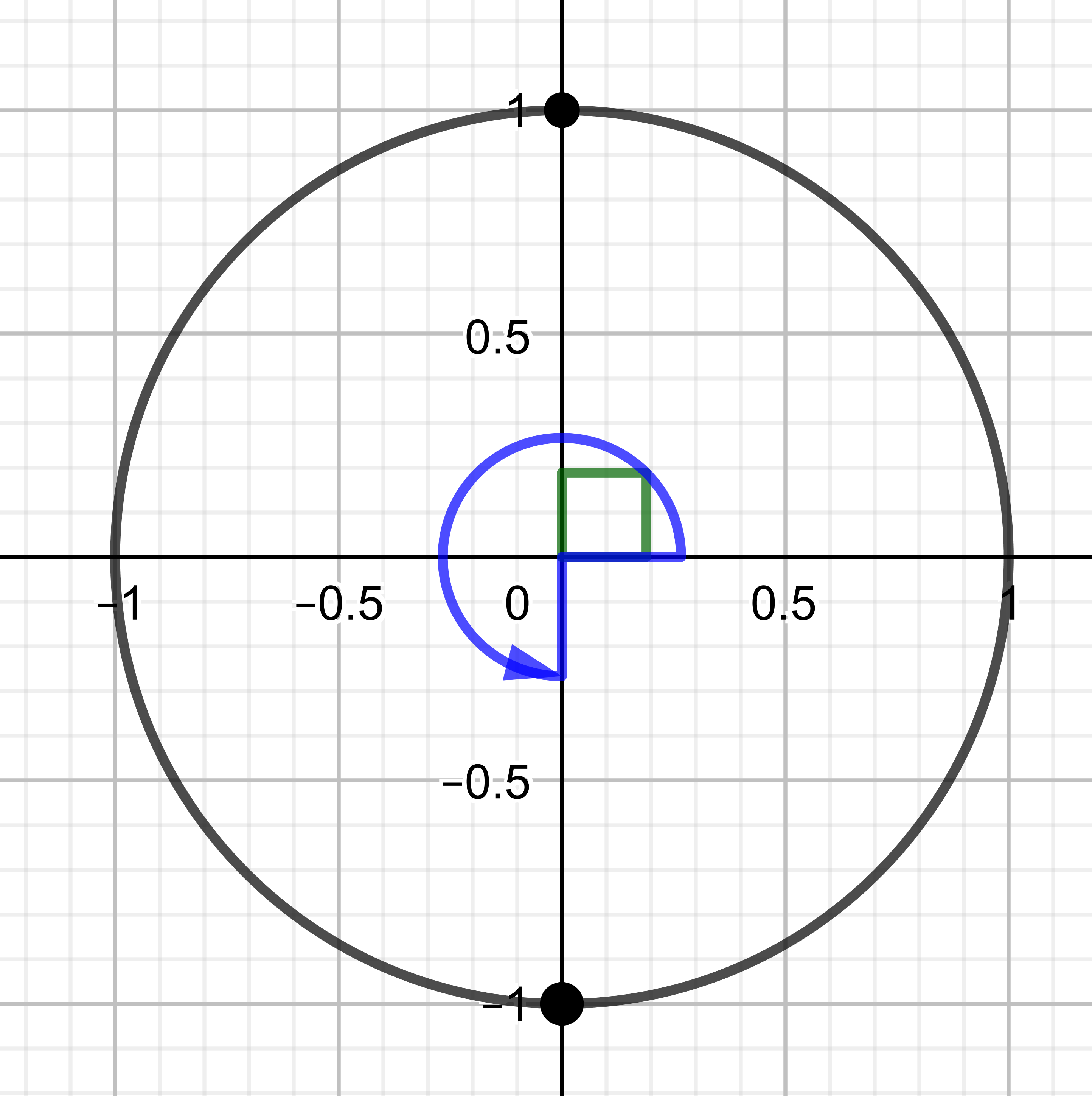
Kun alkuperäisen yhtälön $\sin 2x+2\cos x=0$ ratkaisut sijoittaa yksikköympyrään, niin huomaa, että kosiniyhtälöstä tulleet ratkaisut sisältävät jo siniyhtälönkin ratkaisut, joten yhtälön $\sin 2x+2\cos x=0$ ratkaisut ovat $x=\dfrac{\pi}{2}+n\cdot \pi$, missä $n$ on kokonaisluku. (1 p.)
a) Derivoi $h(x)=\cos^2x$.
b) Määritä funktion $f(x)=\tan(x)$ kuvaajalle pisteeseen $\left(\frac{\pi}{3},\sqrt{3}\right)$ piirretyn tangentin yhtälö.
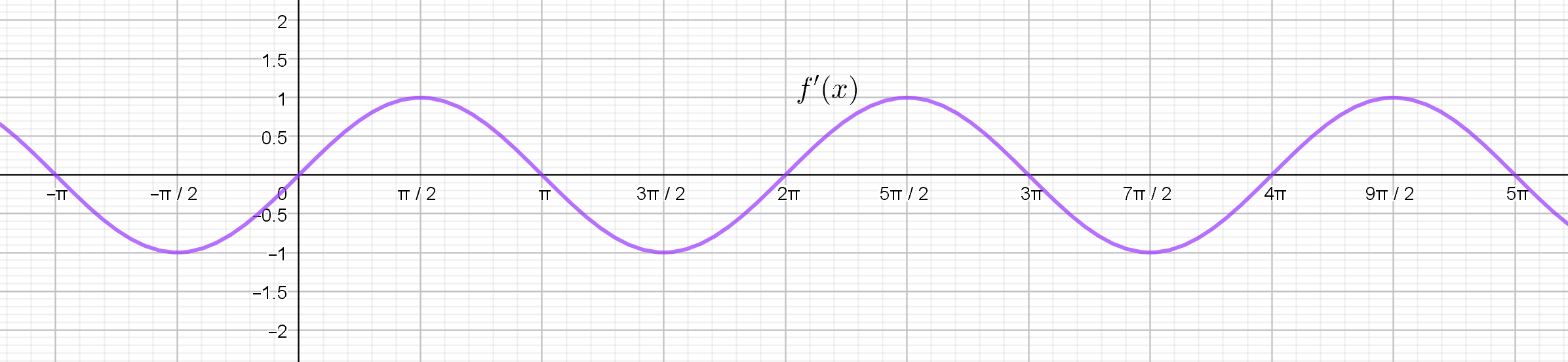
c) Ohessa on erään trigonometrisen funktion $f(x)$ derivaattafunktion $f'(x)$ kuvaaja. Määritä sen avulla alkuperäisen funktion $f(x)$ maksimikohdat.
a) $h(x)=\cos^2x=(\cos x)^2$, jolloin $h'(x)=2\cos x\cdot (D(\cos x))=2\cos x\cdot (-\sin x)=-2\sin x\cos x=-\sin 2x$. (Saatu oikein sisäfunktion derivaatta (1 p.), vastaus (1 p.) (Myös muoto $-2\sin x\cos x$ kelpaa).)
b) Tangentin kulmakerroin on derivaatan arvo ko. kohdassa. Derivoidaan $f(x)$.
$f'(x)=\dfrac{1}{\cos^2(x)}$ tai $f'(x)=1+\tan^2(x)$, jolloin $f'\left( \frac{\pi}{3}\right)=1+\left(\tan\left(\frac{\pi}{3}\right)\right)^2=1+\left( \sqrt{3} \right)^2=4$. (1 p.)
Tangentin yhtälö on siis $y-\sqrt{3}=4(x-\frac{\pi}{3})$ eli $y=4x+\sqrt{3}-\frac{4\pi}{3}.$ (1 p.)
c) Derivaattafunktion nollakohdat ovat alkuperäisen funktion ääriarvokohtia. (1 p.) Näistä ne, joissa derivaatan arvo muuttuu positiivisesta negatiiviseksi, ovat funktion maksimikohtia. Kyseisessä kuvaajassa näitä ovat $\ldots,-\pi, \pi, 3\pi,\ldots$ eli maksimikohdat ovat muotoa $x=\pi+n\cdot 2\pi$, missä $n$ on kokonaisluku. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
