Testi on tarkoitettu kisallioppiminen.fi-sivun MAA7-kurssin itsearviointiin.
a) Olkoon $f(x)=x^2-1$ ja $g(x)=3x+5$. Määritä $(f\circ g)(x)$ ja $(g\circ f)(x)$.
b) Olkoon $h(x)=\dfrac{3}{\sin^2x}$. Määritä funktiosta sisä- ja ulkofunktiot kahdella eri tavalla.
c) Ohessa on eräiden funktioiden $f(x)$ ja $g(x)$ kuvaajat. Määritä kuvaajien avulla $f(g(2))$ ja $(g\circ f)(1)$.


a) $(f\circ g)(x)=f(g(x))=f(3x+5)=(3x+5)^2-1=9x^2+30x+24$ (1 p.) ja
$(g\circ f)(x)=g(f(x))=g\left(x^2-1\right)=3\left(x^2-1\right)+5=3x^2-3+5=3x^2+2$. (1 p.)
b) Tutkitaan funktiota $h(x)=\dfrac{3}{\sin^2x}$. Ulko- ja sisäfunktiot voi määrittää esimerkiksi seuraavasti:
$u(x)=\dfrac{3}{x}$ ja $s(x)=\sin^2x$ tai $u(x)=\dfrac{3}{x^2}$ ja $s(x)=\sin x$. (Toimiva sisä- ja ulkofunktio (1 p.)/pari.)
c) Määritetään aluksi $f(g(2))$. Etsitään aluksi sisäfunktion $g(x)$ arvo kohdassa $x=2$: $g(2)=1$. Tämä on funktion $f(x)$ muuttuja, eli etsitään sitten funktion $f(x)$ arvo kohdassa $x=1$: $f(1)=0.$ Siis $f(g(2))=0.$ (1 p.)
Samaan tapaan määritetään $(g\circ f)(1)=g(f(1))$. $f(1)=0$, joten $g(f(1))=g(0)=-3$. (1 p.)
Olkoon $f(x)=3x^2-1$ ja $g(x)=\cos x$. Määritä
a) $(f\circ g)'(x)$
b) $(g\circ f)'(x)$.
a) Määritetään aluksi funktioiden $f(x)$ ja $g(x)$ derivaattafunktiot.
$f'(x)=3\cdot 2x=6x$ ja $g'(x)=-\sin x$.
$(f\circ g)'(x)=D(f(g(x)))=D(3\cos^2x-1)=6\cos x\cdot (-\sin x)=-6\sin x\cos x$. (Yhdistetty funktio muodostettu oikein (1 p.), $6\cos x$ (1 p.), vastaus (1 p.))
b) $(g\circ f)'(x)=D(g(f(x)))=D(\cos \left(3x^2-1\right))=-\sin\left( 3x^2-1\right)\cdot 6x=-6x\sin\left( 3x^2-1\right)$. (Yhdistetty funktio muodostettu oikein (1 p.), $-\sin \left(3x^2-1\right)$ (1 p.), vastaus (1 p.))
Tehtävänä on määrittää funktion $f(x)=3\sin(2x)-5$ suurin ja pienin arvo.
a) Määritä funktion $f(x)$ suurin ja pienin arvo käyttämällä tietoa sinifunktion ominaisuuksista.
b) Määritä funktion $f(x)$ suurin ja pienin arvo derivaatan avulla.
Tehtävänä on määrittää funktion $f(x)=3\sin(2x)-5$ suurin ja pienin arvo.
a) Käytetään tietoa sinifunktiosta. Sini saa arvot väliltä $[-1,1]$, eli $$-1\leq \sin (2x)\leq1.$$ (1 p.)
Kertomalla kaksoisepäyhtälöä luvulla $3$ saadaan $$-3\leq 3\sin (2x)\leq 3.$$ (1 p.)
Lisäämällä kaksoisepäyhtälöön luvun $-5$ saadaan $$-8\leq 3\sin (2x) -5\leq -2,$$ eli funktion $f(x)=3\sin(2x) -5$ suurin arvo on $-2$ ja pienin arvo on $-8$. (1 p.)
b) Hahmotellaan funktion $f(x)$ kuvaaja.
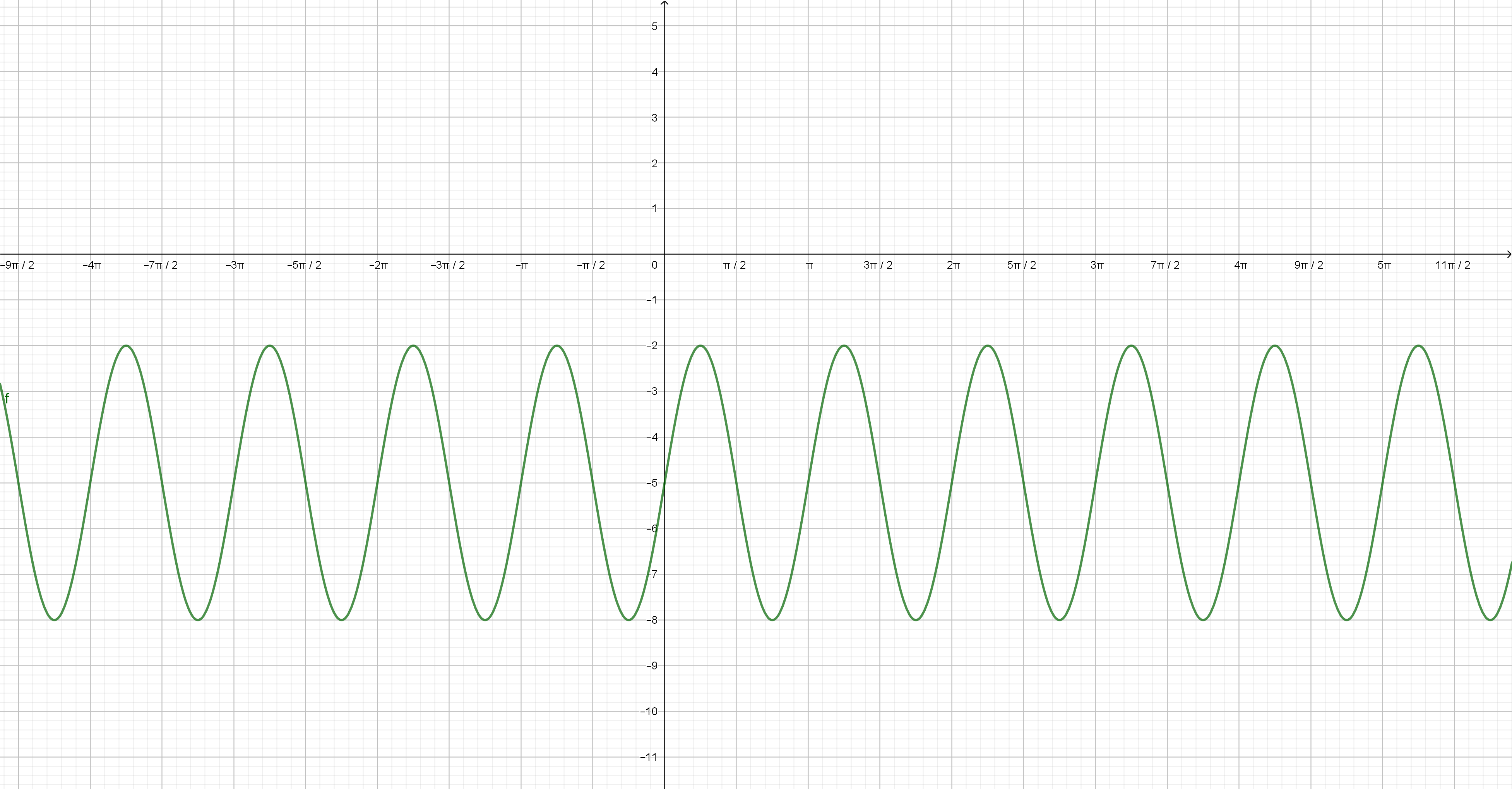
Huomataan, että funktio $f(x)$ on jaksollinen funktio. Riittää siis tarkastella funktiota jollain jakson sisältävällä välillä, esim. välillä $[0,\pi]$. (1 p.)
Suljetulla välillä jatkuva ja vastaavalla avoimella välillä derivoituva funktio saa suurimman ja pienimmän arvonsa välin päätepisteissä tai derivaatan nollakohdissa, jotka kuuluvat tarkasteluvälille. Derivoidaan $f(x)$ ja määritetään derivaatan nollakohdat, jotka kuuluvat välille $]0,\pi[$.
$f'(x)=3\cos(2x)\cdot 2=6\cos (2x)$ ja yhtälön $f'(x)=0$ ratkaisut ovat $2x=\pm \frac{\pi}{2}+n2\pi$, eli $2x=\frac{\pi}{2}+n\pi$, joten $x=\frac{\pi}{4}+n\frac{\pi}{2}$. Näistä välille $]0,\pi[$ kuuluvat $x=\frac{\pi}{4}$ ja $x=\frac{3\pi}{4}$ ($n$:n arvoja 0 ja 1 vastaavat ratkaisut). Muita ei ole, koska jos $n=-1$, niin $x=-\frac{\pi}{4}$ ja toisaalta jos $n=2$, niin $x=\frac{5\pi}{4}$. (1 p.)
Lasketaan funktion $f(x)$ arvo kohdissa $x=0, x=\frac{\pi}{4}$, $x=\frac{3\pi}{4}$ ja $x=\pi$ ja katsotaan, mikä arvoista on suurin ja mikä pienin.
$f(0)=3\sin(2\cdot 0)-5=3\cdot 0-5=-5$
$f\left( \frac{\pi}{4}\right)=3\sin\left( 2\cdot \frac{\pi}{4}\right)-5=3\sin\left( \frac{\pi}{2}\right)-5=3\cdot 1-5=-2$
$f\left( \frac{3\pi}{4}\right)=3\sin\left( 2\cdot \frac{3\pi}{4}\right)-5=3\left( \frac{3\pi}{2} \right)-5=3\cdot (-1)-5=-8$
$f(\pi)=3\sin(2\pi)-5=3\cdot 0-5=-5.$
Suurin ja pienin arvo näyttävät järkeviltä, kun niitä verrataan ratkaisun alussa piirrettyyn kuvaajaan.
Vastaus: Suurin arvo on $-2$ ja pienin arvo on $-8$. (1 p.)
Huom. Jälkimmäinen tapa on aika paljon työläämpi kuin a-kohdan tapa. Kuitenkin jos funktion lauseke on monimutkaisempi funktio, on b-kohdan tapa ainoa toimiva.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
