Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA8-kurssin itsearviointiin.
a) Millä muuttujan $x$ arvoilla lauseke $\sqrt{-x^2+9}$ on määritelty?
b) Ratkaise yhtälö $$\sqrt{x+1}=x-1.$$
a) Parillinen juurifunktio on määritelty, kun juurrettava on epänegatiivinen. Siis $-x^2+9\geq 0$. (1 p.)
Ratkaistaan lausekkeen $-x^2+9$ nollakohdat. Saadaan
\(\begin{align*} -x^2+9&=0\\ x^2&=9\\ x&=\pm\sqrt{9}\\ x&=\pm3. \end{align*}\)
Hahmotellaan kuvaaja.
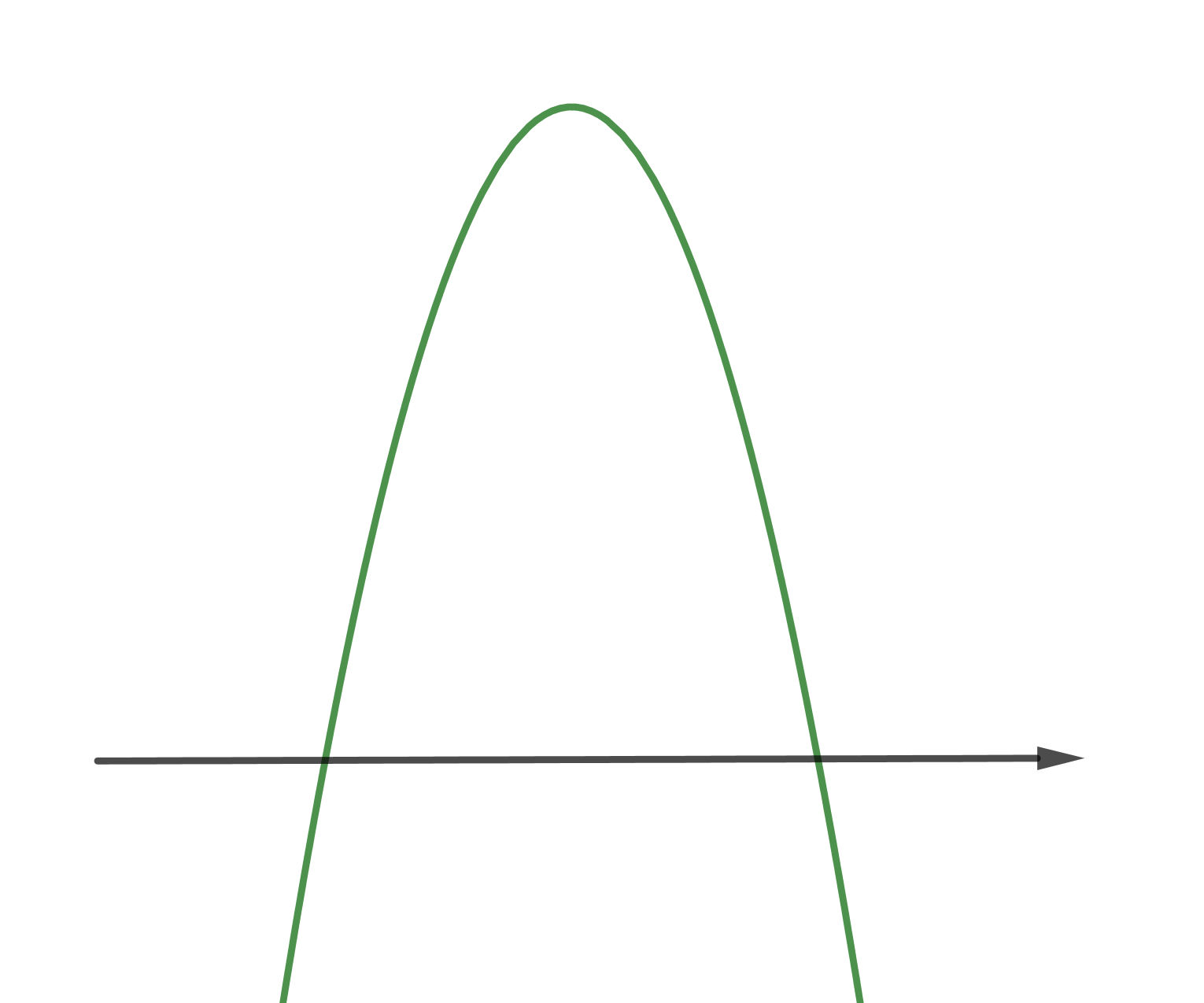
(1 p.)
$-x^2+9\geq0$, kun $-3\leq x\leq 3$, eli $\sqrt{-x^2+9}$ on määritelty, kun $-3\leq x\leq 3$. (1 p.)
b) Yhtälön voi ratkaista joko tarkastelemalla ensin määrittely- ja neliöönkorotusehdot tai tarkistamalla lopuksi, kelpaako ratkaisukandidaatit todella ratkaisuiksi. Tehdään nyt jälkimmäinen tapa.
\(\begin{align*} \sqrt{x+1}&=x-1 \quad || ()^2\\ x+1&=(x-1)^2\\ x+1&=x^2-2x+1\\ x^2-3x&=0. \\ x(x-3)&=0\\ x&=0 \text{ tai }x-3=0 \text{ eli }x=3. \end{align*}\)(Neliöönkorotus oikein (1 p.)
Tarkistus: $x=0$:
$\sqrt{0+1}=0-1$ eli $1=-1$ epätosi. Siis $x=0$ ei ole ratkaisu. (1 p.) Pisteen saisi myös määrittely- ja neliöönkorotusehdoista.
$x=3$:
$\sqrt{3+1}=3-1$ eli $2=2$ tosi.
Vastaus: $x=3$. (1 p.)
Olkoon $f(x)=\sqrt{3x-1}$ ja $g(x)=x^2-1$.
a) Määritä $f'(3)$.
b) Määritä $D((f\circ g)(x))$.
a) Lausutaan $f(x)$ murtopotenssina. $f(x)=(3x-1)^{\frac{1}{2}}$. (1 p.)
Derivoidaan $f(x)$. $f'(x)=\frac{1}{2}\cdot (3x-1)^{-\frac{1}{2}}\cdot 3=\dfrac{3}{2\sqrt{3x-1}}$. (1 p.)
$f'(3)=\dfrac{3}{2\sqrt{3\cdot 3-1}}=\dfrac{3}{2\sqrt{8}}=\dfrac{3}{4\sqrt{2}}.$ (1 p.)
b) Muodostetaan $(f\circ g)(x)$. $f(g(x))=\sqrt{3(x^2-1)-1}=\sqrt{3x^2-3-1}=\sqrt{3x^2-4}$. (1 p.)
Derivaatta on $D((f\circ g)(x))=D(\sqrt{3x^2-4})=\frac{1}{2}(3x^2-4)^{-\frac{1}{2}}\cdot 6x=\dfrac{6x}{2\sqrt{3x^2-4}}=\dfrac{3x}{\sqrt{3x^2-4}}$. (Muistettu sisäfunktion derivaatta (1 p.), vastaus (1 p.))
Määritä funktion $f(x)=x^2\sqrt{-2x+1}$ ääriarvokohdat,
a) tutkimalla funktion $f(x)$ derivaattaa
b) käyttämällä tietoa, että $x^2=\sqrt{x^4}$, soveltamalla juuren laskusääntöjä ja käyttämällä tietoa, että yhdistetyn funktion $\sqrt{g(x)}$ ääriarvokohdat ovat samat kuin sisäfunktion $g(x)$.
a) Funktio $f(x)$ on määritelty, kun $-2x+1\geq 0$ eli $x\leq \frac{1}{2}$. Derivoidaan $f(x)$.
$f'(x)=2x\sqrt{-2x+1}+x^2\cdot\frac{1}{2}(-2x+1)^{-\frac{1}{2}}\cdot (-2)=^{\sqrt{-2x+1})}2x\sqrt{-2x+1}-\dfrac{x^2}{\sqrt{-2x+1}}=\dfrac{2x(-2x+1)-x^2}{\sqrt{-2x+1}}=\dfrac{-4x^2+2x-x^2}{\sqrt{-2x+1}}=\dfrac{-5x^2+2x}{\sqrt{-2x+1}}$, $x<\frac{1}{2}$. (1 p.)
Määritetään derivaatan nollakohdat. Osamäärä on nolla, kun osoittaja on nolla.
\(\begin{align*} -5x^2+2x&=0\\ x(-5x+2)&=0\\ x&=0 \text{ tai }-5x+2=0 \text{ eli } x=\dfrac{2}{5}. \end{align*}\)
Laaditaan merkki- ja kulkukaavio. Koska derivaattafunktion nimittäjä on aina positiivinen, niin osoittaja määrää derivaatan merkit. Osoittaja on alaspäin aukeava paraabeli, joka saa positiivisia arvoja nollakohtien välissä. Muualla arvot ovat negatiivisia.
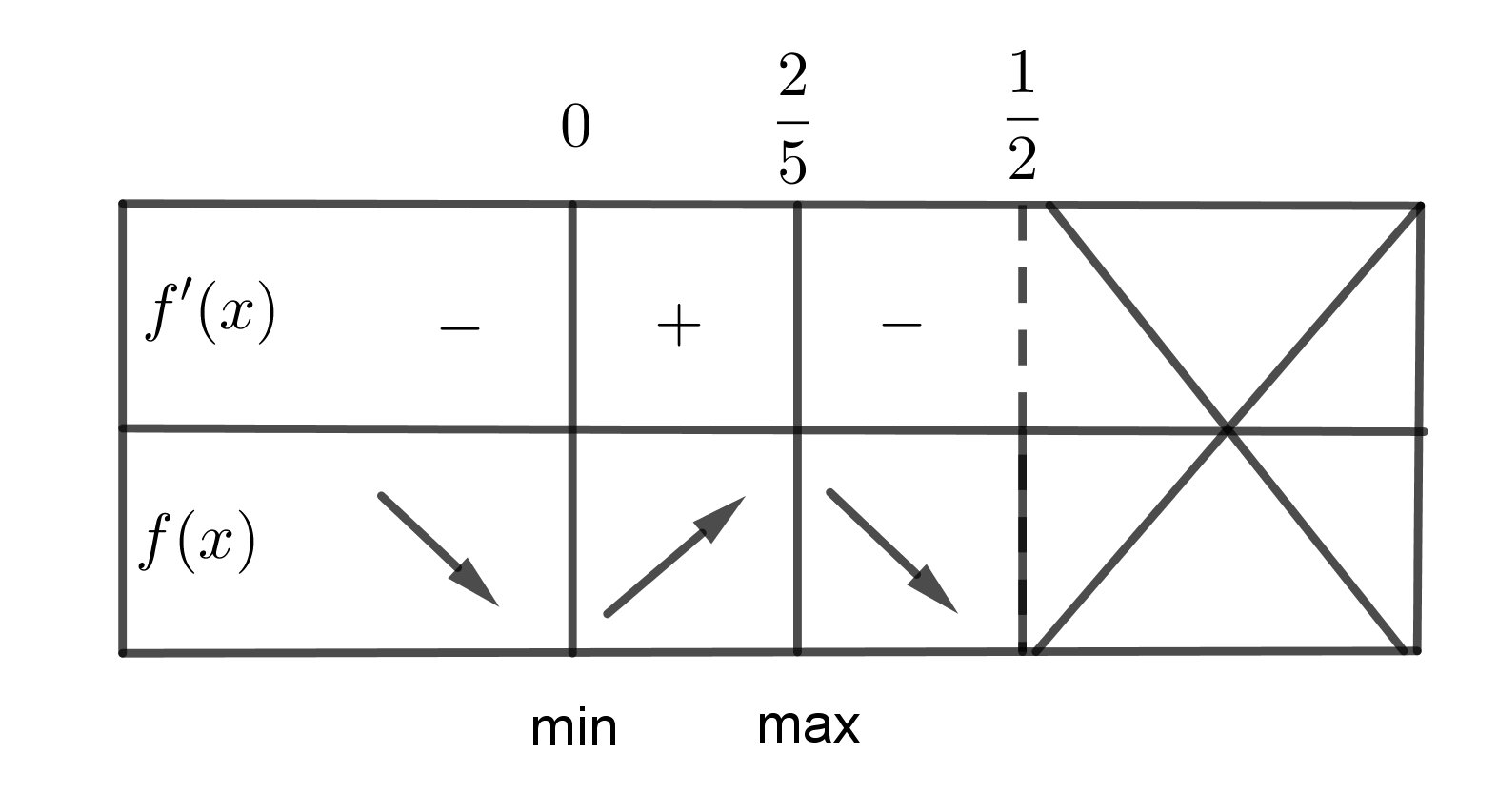(1 p.)
Kulkukaavion perusteella funktiolla on minimikohdat $x=0$ (derivaatan nollakohta) ja $x=1/2$ (välin päätepiste) ja maksimikohta $x=\frac{2}{5}$. (1 p.)
b) Muokataan funktion $f(x)$ lauseketta. $$f(x)=x^2\sqrt{-2x+1}=\sqrt{x^4}\sqrt{-2x+1}=\sqrt{x^4(-2x+1)}=\sqrt{-2x^5+x^4}.$$ (1 p.)
Tarkastellaan sisäfunktiota $g(x)=-2x^5+x^4$. $g'(x)=-2\cdot5x^4+4x^3=-10x^4+4x^3$. Derivaatan nollakohdat:
\(\begin{align*} -10x^4+4x^3&=0\\ x^3(-10x+4)&=0\\ x^3&=0 \text{ tai } -10x+4=0\\ x&=0 \text{ tai } x=\dfrac{2}{5}. \end{align*}\)
Perustellaan derivaatan merkit testipisteillä.
$g'(-1)=-14<0$
$g'(\frac{1}{5}=0{,}016>0$
$g'(0{,}45)=-0{,}045\ldots<0$. (1 p.)
Merkki- ja kulkukaavio:
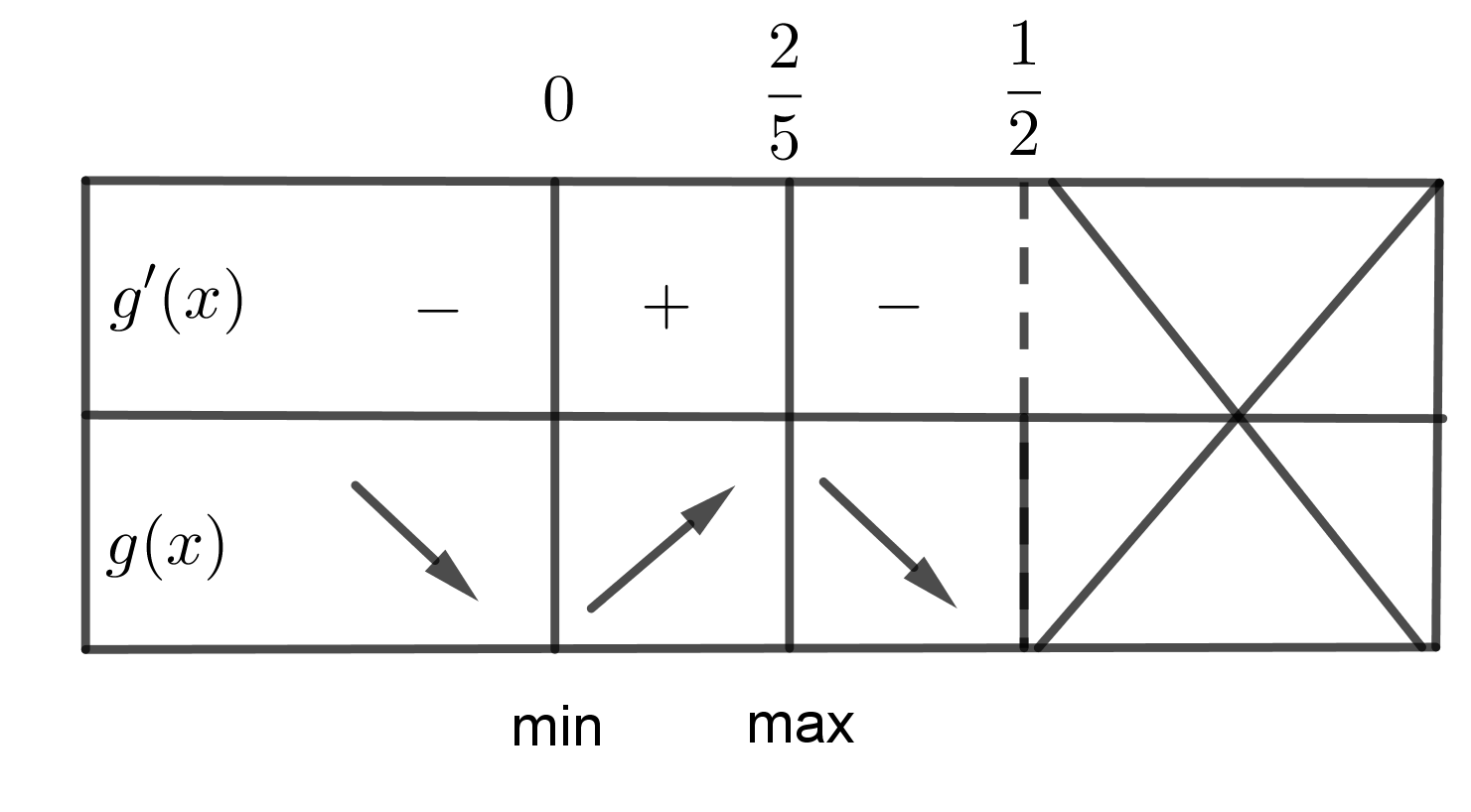
Kulkukaavion perusteella funktiolla $g(x)$ eli myös funktiolla $f(x)$ on minimikohdat $x=0$ ja $x=1/2$ ja maksimikohta $x=\frac{2}{5}$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: