Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA8-kurssimateriaalin itsearviointiin.
Tarkastellaan funktiota $f(x)=\ln(x)+2x$.
a) Osoita, että funktiolla $f(x)$ on olemassa käänteisfunktio.
b) Piirrä funktion ja sen käänteisfunktion kuvaajat samaan koordinaatistoon.
c) Onko käänteisfunktion kuvaajalla piste $(2e,e)$? Perustele.
a) Funktio on määritelty, kun $x>0$. Osoitetaan, että funktio on aidosti monotoninen, koska tällöin sillä on olemassa käänteisfunktio.
$f'(x)=\frac{1}{x}+2$. Koska $x>0$, niin $\frac{1}{x}>0$, joten $\frac{1}{x}+2=f'(x)>0$. (1 p.)
Siis $f$ on aidosti kasvava ja käänteisfunktio on olemassa. (1 p.)
b) Piirretään kuvaajat. Käänteisfunktion kuvaaja saadaan peilaamalla funktion kuvaaja suoran $y=x$ suhteen.
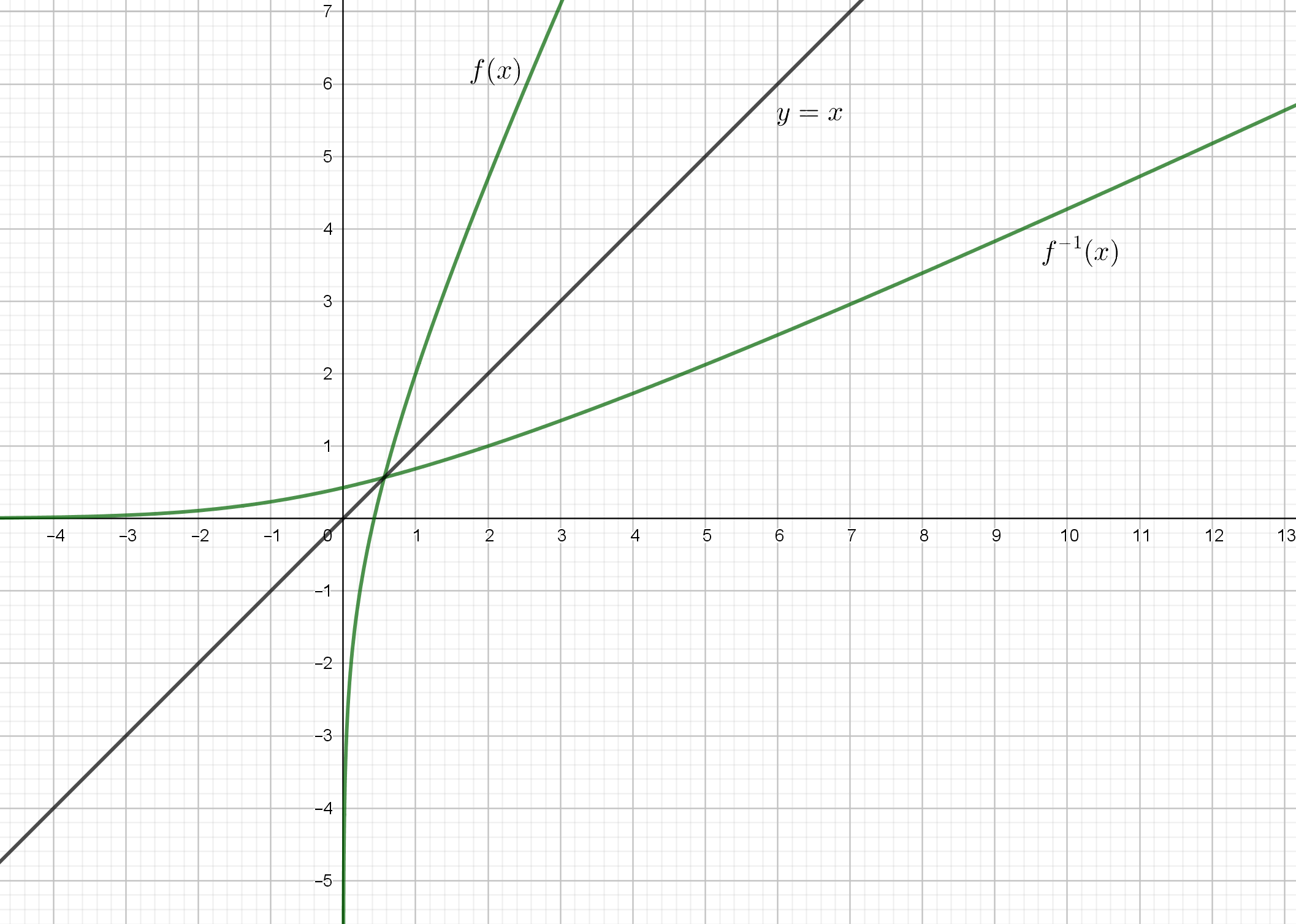(2 p.)
c) Jos käänteisfunktion kuvaajalla on piste $(2e,e)$, niin tällöin funktion kuvaajalla on piste $(e,2e)$. (1 p.)
Lasketaan funktion arvo kohdassa $x=e$.
$f(e)=\ln(e)+2\cdot e=1+2e\neq 2e$, eli ei ole. (1 p.)
a) Tutki, onko $g(x)=\frac{1}{1+x}$ funktion $f(x)=\frac{x}{1-x}$ käänteisfunktio.
b) Muodosta funktion $f(x)=\sqrt[3]{4x+1}$ käänteisfunktion lauseke.
a) Tutkitaan, päteekö $g(f(x))=x$ ja $f(g(x))=x$.
$g(f(x))=\frac{1}{1+ \frac{x}{1-x}}=\frac{1}{\frac{1-x+x}{1+x}}=1+x\neq x$ eli ei ole. (Yhdistetyn funktion muodostamisen idea (1 p.), sijoitus oikein (1 p.), vastaus (1 p.))
b) Muodostetaan käänteisfunktion lauseke ratkaisemalla yhtälöstä $f(a)=b$ kirjain $a$. Saadaan
\(\begin{align*} \sqrt[3]{4a+1}&=b\\ 4a+1&=b^3\\ 4a&=b^3-1\\ a&=\frac{b^3-1}{4}. \end{align*}\)(Muodosta $4a+1=b^3$ (1 p.), ratkaisu (1 p.))
Käänteisfunktion lauseke on $f^{-1}(x)=\frac{x^3-1}{4}$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: