Tämä testi suositellaan tehtäväksi tietokoneella tai tablet-laitteella.
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Tutki alla olevien liukukytkimien avulla funktion $f(x)=kx+b$ kuvaajan muotoa muuttujien $k$ ja $b$ eri lukuarvoilla.
a) Kuvaile sanallisesti, miten muuttujien $k$ ja $b$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin.
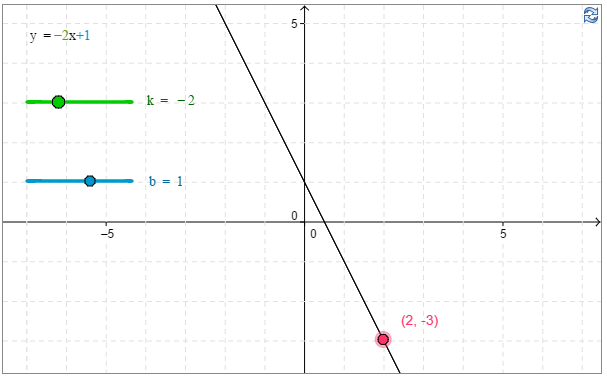
b) Ratkaise graafisesti (liikuttamalla punaista pistettä käyrällä) yhtälö $-3=-2x+1$.
c) Määritä graafisesti $f(2,\!5)$, kun $f(x)=3x-4$.
a)
- Muotoa $f(x)=kx+b$ olevan funktion kuvaaja on suora.
- Ensimmäisen asteen termin kerroin $k$ (jota kutsutaan kulmakertoimeksi) vaikuttaa suoran "jyrkkyyteen". Kun $k>0$, suora on nouseva suora, ja kun $k<0$, suora on laskeva suora. \(\require{color}\color{red}{\text{(+1p)}}\)
- Vakiotermi $b$ vaikuttaa siihen, millä "korkeudella" suora on. Havaitaan, että suora leikkaa $y$-akselin aina pisteessä$(0,b)$. \(\require{color}\color{red}{\text{(+1p)}}\)
b) Kuvaajan avulla havaitaan, että yhtälön $-3=-2x+1$ ratkaisu on \(\underline{\underline{x \approx 2}}\). \(\require{color}\color{red}{\text{(+2p)}}\)
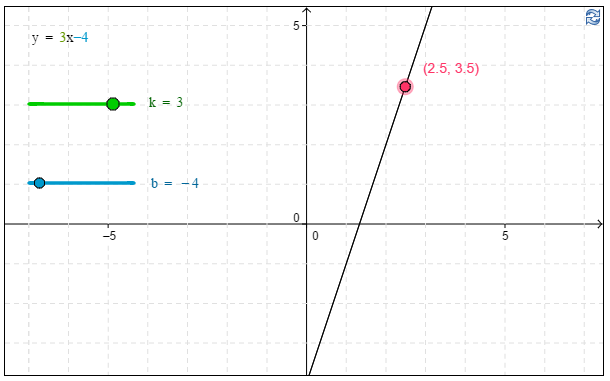
c) Kuvaajan avulla havaitaan, että funktion arvo \(f(2,\!5)\approx\underline{\underline{3,\!5}}\), kun $f(x)=3x-4$ (hyväksytään vastaus väliltä $[3,\!4;3,\!6]$). \(\require{color}\color{red}{\text{(+2p)}}\)
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Tutki alla olevien liukukytkimien avulla funktion $f(x)=ax^2+bx+c$ kuvaajan muotoa muuttujien $a$, $b$ ja $c$ eri lukuarvoilla.
a) Kuvaile sanallisesti, miten muuttujien $a$, $b$ ja $c$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin.
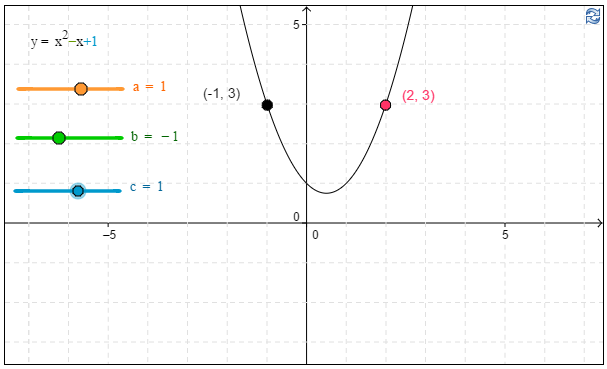
b) Ratkaise graafisesti (liikuttamalla punaista pistettä käyrällä) yhtälö $3=x^2-x+1$.
c) Määritä graafisesti $f(-1)$, kun $f(x)=-2x^2+3x+5$.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a)
- Muotoa $f(x)=ax^2+bx+c$ olevan funktion kuvaaja on paraabeli.
- Toisen asteen termin kerroin $a$ vaikuttaa paraabelin aukeamissuuntaan. Kun $a>0$, paraabeli on ylöspäin aukeava, ja kun $a<0$, paraabeli on alaspäin aukeava. \(\require{color}\color{red}{\text{(+1p)}}\)
- Ensimmäisen asteen termin kerroin $b$ vaikuttaa paraabelin sijaintiin sekä pysty- että sivusuunnassa. Vakiotermi $c$ vaikuttaa paraabelin sijaintiin vain pystysuunnassa. \(\require{color}\color{red}{\text{(+1p)}}\)
- Havaitaan, että paraabeli leikkaa $y$-akselin aina pisteessä$(0,c)$.
b) Kuvaajan avulla havaitaan, että yhtälön $3=x^2-x+1$ ratkaisu on \(\underline{\underline{x \approx -1}}\) tai \(\underline{\underline{x \approx 2}}\). \(\require{color}\color{red}{\text{(+2p)}}\)
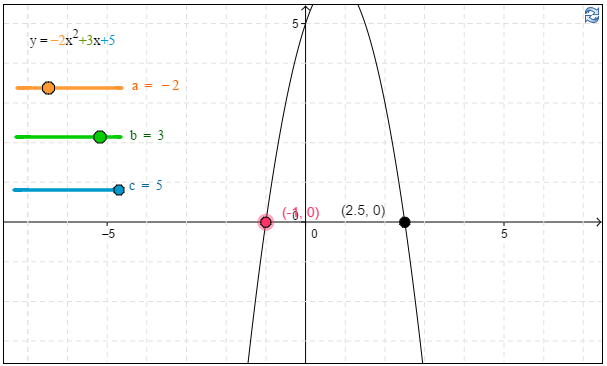
c) Kuvaajan avulla havaitaan, että funktion $f(x)=-2x^2+3x+5$ arvo \(f(-1)\approx\underline{\underline{\ 0\ }}\). \(\require{color}\color{red}{\text{(+2p)}}\)
Yökaudet tietokoneita pelaileva opiskelija huomasi, että energiajuomien nauttiminen iltaisin vaikuttaa siihen, kuinka monta tuntia pelejä jaksaa pelata. Pelaamisaika noudatti likimain funktiota $T(j)=-0,5j^2+1,6j+2,8$, missä $j$ on juotujen juomatölkkien lukumäärä.
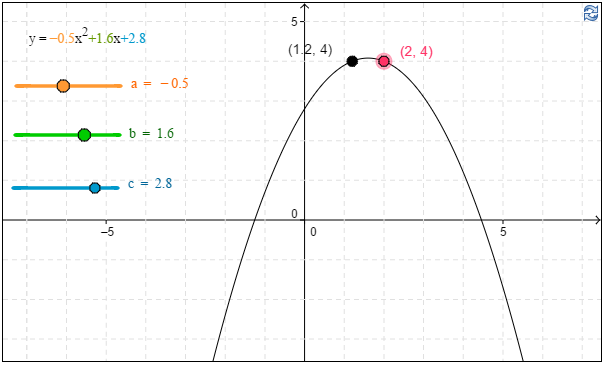
a) Kuinka monta tuntia opiskelija jaksoi yöllä pelata, jos hän joi kaksi energiajuomatölkkiä?
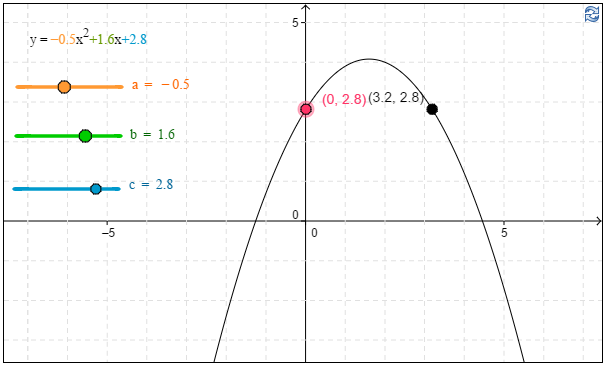
b) Kuinka monta tuntia opiskelija jaksoi pelata ilman energiajuomaa?
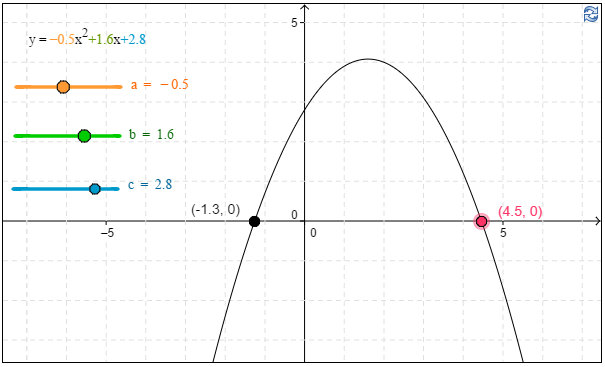
c) Kuinka monen tölkillisen nauttiminen aiheuttaa niin kovat pärinät, ettei opiskelija pysty pelaamaan ollenkaan (eli $T(j)=0$)?
Laske vastaukset, mutta käytä alla olevaa kuvaajaa tilanteen hahmottamiseen ja vastauksesi tarkistamiseen.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
\( \require{color} \begin{align*} \textbf{a) }T(2)&=-0,5\cdot2^2+1,6 \cdot 2 +2,8 \qquad \color{red} \text{(+1p)}\\ &=4 \end{align*}\)
Vastaus: Neljä tuntia. \(\require{color}\color{red} \text{(+1p)}\)
\( \require{color} \begin{align*} \textbf{b) }T(0)&=-0,5\cdot0^2+1,6 \cdot 0 +2,8 \qquad \color{red} \text{(+1p)}\\ &=2,8 \end{align*}\)
Vastaus: 2,8 tuntia (2 tuntia 48 minuuttia). \(\require{color}\color{red} \text{(+1p)}\)
\( \require{color} \begin{align*} \textbf{c) }\qquad \qquad \qquad \quad T(j)&=0\\-0,5j^2+1,6j+2,8&=0 & &\Big|\Big|j=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\\ & && \Big|\Big| a=-0,5\ ;\ b=1,6\ ;\ c=2,8 \end{align*}\)
\( \require{color} \begin{align*} j&=\dfrac{-1,6 \pm \sqrt{1,6^2 -4 \cdot (-0,5) \cdot 2,8}}{2 \cdot (-0,5)} \qquad \color{red} \text{(+1p)} \\ j&=\dfrac{-1,6 \pm \sqrt{8,16}}{-1} \\ j&=\dfrac{-1,6 \pm 2,856...}{-1} \\ j&=-1,256... \ \text{ tai }\ j=4,456... \end{align*}\)
Vastaus: Juotuaan noin 4,5 tölkkiä opiskelija ei pysty enää pelaamaan. \(\require{color}\color{red} \text{(+1p)}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
