Tämä testi mittaa osaamistasi tasaisen ja muuttuvan liikkeen mallin tunnistamisesssa sekä molempiin liiketiloihin liittyvien suureyhtälöiden käytössä.
Kuvassa on esitetty suoraviivaisesti liikkuvan kappaleen paikka ajan funktiona.
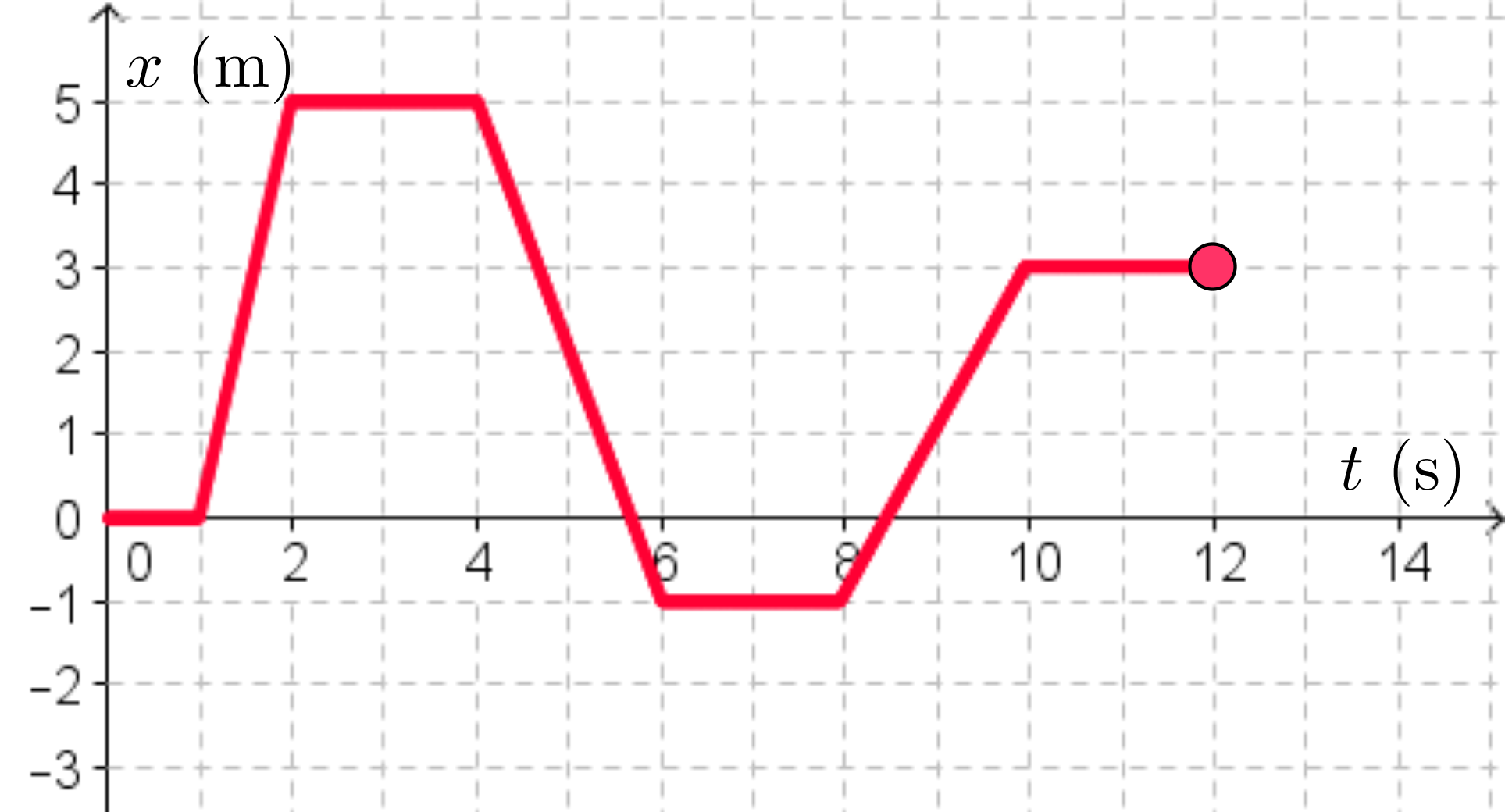
Selvitä kuvaa tarkastelemalla
a) kappaleen siirtymä aikavälillä \(0,0 \text{ s} \ldots 10 \text{ s}\)
b) kappaleen aikavälillä \(0,0 \text{ s} \ldots 12 \text{ s} \) kulkema matka.
c) kappaleen suurin nopeus.
a)
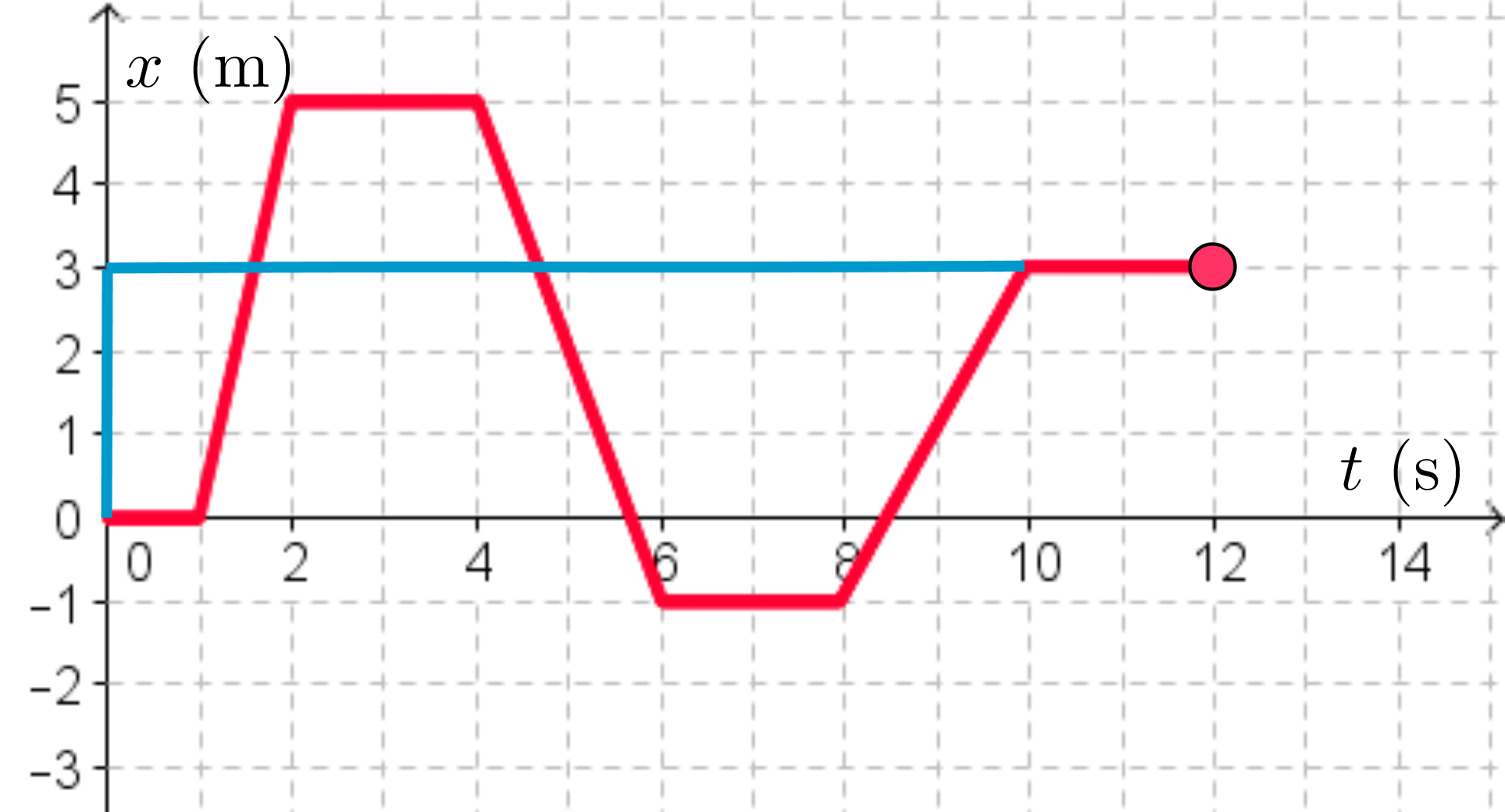
Kuvaajasta huomataan, että
\(\Delta x = x_1 - x_0 \qquad \qquad \color{Red}{\text{(+1p)}} \\ \quad \ \ = 3,0 \text{ m} - 0,0 \text{ m} \\ \quad \ \ = \underline{\underline{3,0 \text{ m}}} \qquad \ \ \qquad \color{Red}{\text{(+1p)}}\)
b) Katsojaan kuvaajasta kappaleen etenemä matka oheisilla aikaväleillä
\(0,0 \text{ s} \ldots 1,0 \text{ s},\ \ \ \quad s_1=0,0 \text{ m} \\ 1,0 \text{ s} \ldots 2,0 \text{ s},\ \ \ \quad s_2=5,0 \text{ m} \\ 2,0 \text{ s} \ldots 4,0 \text{ s}, \ \ \ \quad s_3=0,0 \text{ m} \\ 4,0 \text{ s} \ldots 6,0 \text{ s}, \ \ \ \quad s_4=6,0 \text{ m} \\ 6,0 \text{ s} \ldots 8,0 \text{ s}, \ \ \ \quad s_5=0,0 \text{ m} \\ 8,0 \text{ s} \ldots 10 \text{ s}, \ \ \ \ \ \quad s_6=4,0 \text{ m} \\ 10,0 \text{ s} \ldots 12 \text{ s}, \ \ \ \quad s_7=0,0 \text{ m} \quad \color{Red}{\text{(+1p)}}\)
Kappale etenee aikaväillä \(0,0 \text{ s} \ldots 12 \text{ s}\)yhteensä
\(s_{kok}=5,0 \text{ m} + 6,0 \text{ m} +4,0 \text{ m} = \underline{\underline{15 \text{ m}}} \quad \color{Red}{\text{(+1p)}}\)
c) Kappaleen nopeus on suurimmillaan, kun suoran fysikaalinen kulmakerroin on suurin.
Huomataan, että suoran kulmakerroin on suurin ajanjaksolla \(0,0 \text{ s} \ldots 2,0 \text{ s}\)
\(v=\dfrac{\Delta v}{\Delta t} \qquad \qquad \color{Red}{\text{(+1p)} \color{Black}{\\ \ \ =\dfrac{x_2-x_1}{t_2-t_1}} \\ \ \ \color{Black}{= \dfrac{5,0 \text{ m} - 0,0 \text{ m}}{2,0 \text{ s } - 1,0 \text{ s } } }\\ \ \ \color{Black}{= \underline{\underline{ 5,0 \text{ m/s}}} }\qquad \qquad \color{Red}{\text{(+1p)}}}\)
Autoa jarrutetaan 13 sekunnin ajan, jolloin sen nopeus pienenee arvosta 100 km/h arvoon 60 km/h.
Jos jarrutus tapahtuu tasaisesti, niin kuinka pitkän matkan auto etenee jarrutuksen aikana?

Tapa 1.
Kirjataan lähtöarvot ylös.
\(t=13 \text{ s}, v_0 = 100 \text{ km/h}, v_1=60 \text{ km/h}\)
Lasketaan auton kiihtyvyys
\(a=\dfrac{\Delta v}{\Delta t} \\ =\dfrac{v_1-v_0}{t_1-t_0} \\ =\dfrac{\frac{60}{3,6}\frac{\text{m}}{\text{s}}-\frac{100}{3,6} \frac{\text{m}}{\text{s}}}{13 \text{ s}} \)\(\quad \color{red}{\text{(+1p)}}\)
\(\\\approx \underline{ \underline{-0,855 \frac{\text{m}}{\text{s}}}}\)\(\quad \color{red}{\text{(+1p)}}\)
Jarrutus tapahtuu tasaisesti, joten auto on tasaisesti kiihtyvässä liikkeessä. \(\quad \color{red}{\text{(+1p)}}\)
Kappaleen paikka tasaisesti kiihtyvässä liikkeessä on
\(x=x_0+v_0t+\dfrac{1}{2}at^2\)\(\quad \color{red}{\text{(+1p)}}\)
Sijoitetaan paikan yhtälöön tunnetut arvot.
\(x=0,0 \text{ m}+\dfrac{100}{3,6}\frac{\text{m}}{\text{s}} \cdot 13 \text{ s} + \dfrac{1}{2} (-0,855\frac{\text{m}}{\text{s}^2}) \cdot (13 \text{ s})^2\)\(\quad \color{red}{\text{(+2p)}}\)
\(x\approx 289 \text{ m}\)
Vastaus: Auto etenee noin 290 metriä jarrutuksen aikana. \(\quad \color{red}{\text{(+1p)}}\)
Tapa 2.
Hahmotellaan auton nopeuden kuvaaja (t, v)-koordinaatistoon.
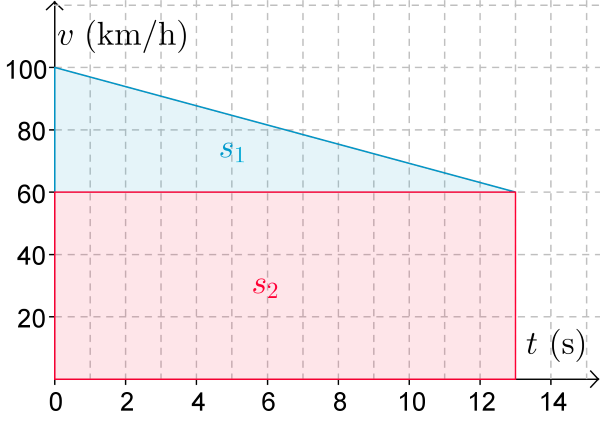 \(\quad \color{red}{\text{(+1p)}}\)
\(\quad \color{red}{\text{(+1p)}}\)
Auton kulkema matka saadaan laskettua graafisesti integroimalla (t, v) -kuvaajan alle jäävä pinta-ala. \(\quad \color{red}{\text{(+1p)}}\)
Kolmiota vastaava matka
\(s_{1}=\dfrac{1}{2}\cdot 13 \text{ s} \dot (\dfrac{100}{3,6} \dfrac{\text{m}}{\text{s}}-\dfrac{60}{3,6}\frac{\text{m}}{\text{s}})\) \(\quad \color{red}{\text{(+1p)}}\)
\(s_1 \approx 72,2 \text{ m}\)
Suorakulmiota vastaava matka
\(s_2=\dfrac{60}{3,6} \frac{\text{m}}{\text{s}} \cdot 13 \text{ s} \approx 216,7 \text{ m}\) \(\quad \color{red}{\text{(+1p)}}\)
Kokonaismatka
\(s_{kok}=s_1+s_2\) \(\quad \color{red}{\text{(+1p)}}\)
\(s_{kok}=72,2 \text{ m} + 216,7 \text{ m}\)
\(s_{kok}\approx 289 \text{ m}\)
Vastaus: Auto etenee noin 290 metriä jarrutuksen aikana. \(\quad \color{red}{\text{(+1p)}}\)
Tennispallo pomppaa lattiasta suoraan ylöspäin nopeudella 5,0 m/s.
Milloin pallo on 1,0 metrin korkeudella?

Kirjataan lähtöarvot ylös.
\(v_0=5,0 \text{ m/s}, \ y=1,0 \text{ m}, \ g=-9,81 \text{ m/s}^2\)
Tennispallo on tasaisesti kiihtyvässä liikkeessä ja sen kiihtyvyys on sama kuin putoamiskiihtyvyys. \(\quad \color{red}{\text{(+1p)}}\)
Kappaleen paikka tasaisesti kiihtyvässä liikkeessä
\(y=v_0t-\dfrac{1}{2}gt^2\) \(\quad \color{red}{\text{(+1p)}}\)
\(-\dfrac{1}{2}gt^2+v_0t-y=0\)
Ratkaistaan paikan yhtälöstä aika \(t\) toisen asteen yhtälön ratkaisukaavan avulla.
\(t=\dfrac{-v_0 \pm \sqrt{v_o^2-4\cdot (-\frac{1}{2}g )\cdot (-y)}}{2 \cdot \frac{1}{2}g}\)\(\quad \color{red}{\text{(+1p)}}\)
\(t= \dfrac{-5,0 \frac{\text{m}}{\text{s}} \pm \sqrt{(5,0\frac{\text{m}}{\text{s}})^2-2 \cdot 9,81\frac{\text{m}}{\text{s}^2} \cdot 1,0 \text{ m}}}{9,81\frac{\text{m}}{\text{s}^2}}\)\(\quad \color{red}{\text{(+1p)}}\)
\(\underline{t_1 \approx 0,273 \text{ s ja } t_2 \approx 0,746 \text{ s}}\) \(\quad \color{red}{\text{(+1p)}}\)
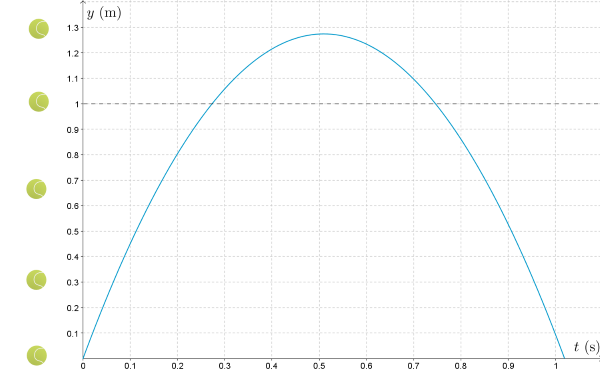
Vastaus: Pallo on korkeudella 1,0 metriä ajanhetkillä 0,27 s ja 0,75 s. \(\quad \color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
