Teoria
Gravitaatiolaki
Newtonin gravitaatiolaki
\(F=\gamma \dfrac{m_1m_2}{r^2}\), jossa
\(\gamma = 6,67384 \cdot 10^{-11} \text{ Nm}^2\text{kg}^{-2}\) gravitaatiovakio.
\(r\) on painopisteiden välinen etäisyys.
\(m_1, \ m_2\) ovat kappaleiden massat.
Gravitaation aiheuttama ympyräliike
Kun Kuu kulkee Maata kiertävällä radalla, niin siihen vaikuttavista voimista ainoa merkityksellinen on
Maan gravitaativoima.
Tarkastellaan Kuun liikettä tasaisena ympyräliikkeenä ja ratkaistaan Kuun ratanopeus Maapallon suhteen.
Gravitaatiovoima \(F_G\)aiheuttaa Maata kiertävälle Kuulle normaalikiihtyvyyden \(a_n = \dfrac{v^2}{r}\).
Olkoon M Maapallon massa ja m Kuun massa.
Maan ja Kuun välinen keskietäisyys on 384 400 km.
Maan säde on noin 6371 km ja Kuun säde 1737 km.
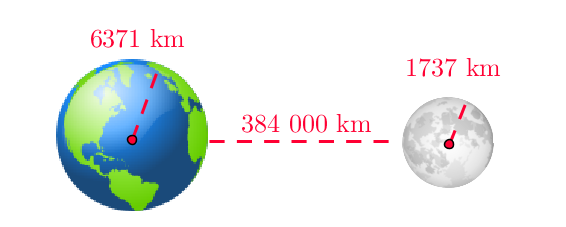
Maan ja Kuun painopisteiden välinen etäisyys on
\(\begin{align*} r&=384 \ 400 \text{ km} + 6371 \text{ km} + 1737 \text{ km} \\ r&=392 \ 508 \text{ km} \\ r&=392 \ 508 \ 000 \text{ m} \end{align*}\)
Newtonin 2. lain eli dynamiikan peruslain mukaan Kuun liikeyhtälö on:
\(\begin{align*} \sum \overline{F}&=m\overline{a} \\ F_G &= ma_n \qquad &&||a_n=\frac{v^2}{r}\\ \gamma \dfrac{mM}{r^2}&=m\dfrac{v^2}{r} \qquad &&||:m \\ \gamma \dfrac{M}{r^2}&=\dfrac{v^2}{r} \qquad &&||\cdot r \\ \gamma\dfrac{M}{r}&=v^2 &&||\sqrt{} \\ v&=\sqrt{\dfrac{\gamma M}{r}} \end{align*}\)
Sijoitetaan lukuarvot.
\(v = \sqrt{\dfrac{6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{ kg}^2} \cdot 5,974 \cdot 10^{24} \text{ kg}}{392 \ 508 \ 000 \text{ m}}}\)
\(v \approx 1007 \text{ m/s}\)
Kuun ratanopeus Maan ympäri on noin 1,007 km/s.
\(\)
Videot
Esimerkit
Esimerkki 1

Apollo 11 oli ensimmäinen Kuun kamaralle laskeutunut miehitetty avaruuslento.
Ennen laskeutumistaan Kuun pinnalle Apollo 11 kiersi Kuuta noin 100 km korkeudella Kuun pinnasta.
Kuinka suuri oli komentoalukseen, jonka massa oli noin 30 000 kg, kohdistuvan gravitaatiovoiman suuruus tällä korkeudella?
Ratkaisu
Kirjataan lähtöarvot
\(r_{kuu} = 1737 \text{ km}, \\ m_{kuu} = 7,342 \cdot 10^{22}\text{ kg}, \\ m_1=30 \ 000 \text{ kg}, \\ h=100 \text{ km}\)
Lasketaan gravitaatiovoiman suuruus
\(F=\gamma \dfrac{m_1 \cdot m_{kuu}}{r^2}\)
\(F=6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{ kg}^2} \cdot \dfrac{30 \ 000 \text{ kg} \cdot 7,342 \cdot 10^{22}\text{ kg}}{(1737 \ 000 \text{ m} + 100 \text{ m})^2}\)
\(F \approx 49 \text{ kN}\)
Vastaus: noin 49 kN
Esimerkki 2
Laske kuinka suuri on omenan putoamiskiihtyvyys Kuun pinnalla.
Ratkaisu
Kirjataan lähtöarvot
\(r_{kuu} = 1737 \text{ km}, \\ m_{kuu} = 7,342 \cdot 10^{22}\text{ kg}\)
Olkoon omenan massa m.
Newtonin 2. lain mukaan omenan liikeyhtälö Kuun pinnalla on:
\(\begin{align*} \sum \overline{F}&=m\overline{a} \\ F&=ma \\ \gamma \dfrac{m\cdot m_{kuu}}{r_{kuu}^2}&=ma \qquad ||:m \\ \gamma \dfrac{m_{kuu}}{r_{kuu}^2}&=a \end{align*}\)
Sijoitetaan tunnetut lukuarvot.
\(a=\gamma \dfrac{m_{kuu}}{r_{kuu}^2}\)
\(a=6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{ kg}^2} \cdot \dfrac{7,342 \cdot 10^{22}\text{ kg}}{(1737 \ 000 \text{ m} )^2}\)
\(a \approx 1,6 \text{ m/s}^2\)
Vastaus: Omenan putoamiskiihtyvyys Kuun pinnalla on noin \(1,6 \text{ m/s}^2\)
