Kaasusäiliön tilavuus on 25 litraa ja paine on 6,0 baaria.
Kuinka suuren tilavuuden kaasu ottaisi normaalissa ilmanpaineessa?

Kirjataan lähtöarvot
\(V_1=25 \text{ l}, \ p_1=6,0 \text{ bar} \\ p_2=1,01325 \text{ bar}\)
Oletetaan, että prosessi on isoterminen. (+1p)
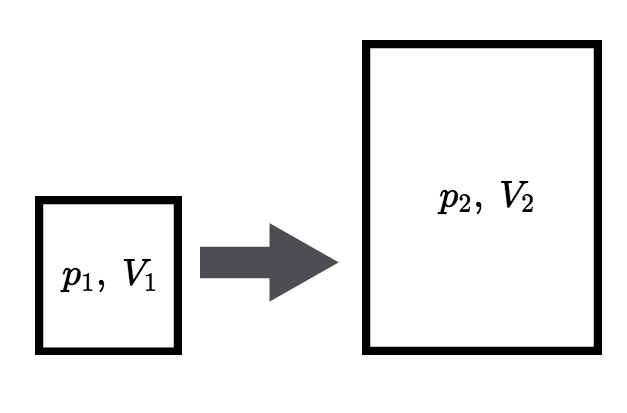
Sovelletaan Boylen lakia \(pV=\text{vakio}\). (+1p)
\(\begin{align} p_1V_1&=p_2V_2 \quad &&||:p_2 \\ V_2 & = \dfrac{p_1V_1}{p_2} \end{align}\) (+2p)
Sijoitetaan lukuarvot ja lasketaan kaasun tilavuus normaalissa ilmanpaineessa.
\(V_2 = \dfrac{6,0 \text{ bar} \cdot 25 \text{ l}}{1,01325 \text{ bar}} \\ V_2 \approx 148 \text{ l}\) (+1p)
Vastaus: Kaasun tilavuus on noin 150 litraa. (+1p)
Saunan, jonka tilavuus on 21 m3 , lämpötila kohoaa tunnin aika +20 celsiusasteesta +75 celsiusasteeseen.
Kuinka paljon saunasta poistuu ilmaa lämmityksen aikana, jos saunassa vallitseva paine pysyy vakiona?

Kirjataan lähtöarvot.
\(V_1=21 \text{ m}^3, \ T_1=(20+273,15)\text{ K}=293,15 \text{ K} \)
\(T_2=(75+273,15)\text{ K} = 348,15 \text{ K}\)
Oletetaan, että prosessi on isobaarinen. (+1p)
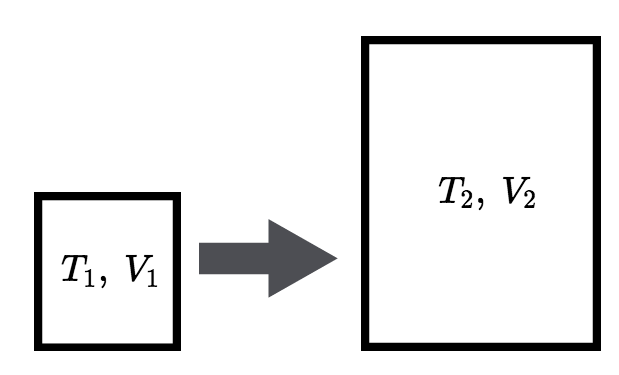
Sovelletaan Gay-Lussacin lakia. (+1p)
\(\begin{align} \dfrac{V_1}{T_1}&=\dfrac{V_2}{T_2} \quad &&|| \cdot T_2 \\ \dfrac{V_1T_2}{T_1}&=V_2 \\ V_2&=\dfrac{V_1T_2}{T_1} \end{align}\) (+2p)
Sijoitetaan tunnetut lukuarvot ja lasketaan ilman tilavuus lopuksi.
\(V_2=\dfrac{21 \text{ m}^3 \cdot 348,15 \text{ K}}{293,15 \text{ K}} \\ V_2 \approx 24,9 \text{ m}^3\) (+1p)
Lasketaan kuinka paljon ilmaa poistuu saunasta.
\(\Delta V=V_2 - V_1 \\ \Delta V = 24,9 \text{ m}^3 - 21 \text{ m}^3\\ \Delta V = 3,9 \text{ m}^3\)
Vastaus: Ilmaa poistuu 3,9 m3 (+1p)
Ilmapallossa on 2,3 litraa ilmaa +22˚C lämpötilassa ja 0,980 baarin paineessa. Mikä on kaasun tilavuus NTP-olosuhteissa?

Kirjataan lähtöarvot
\(V_1=2,3 \text{ l}, \ T_1=(22+273,15)\text{ K}=295,15 \text{ K}, p_1=98 \ 000 \text{ Pa}\)
\(T_2=273,15 \text{ K}, \ p_2 = 101 \ 325 \text{ Pa}\)
Sovelletaan ideaalikaasun tilanyhtälöä \(\dfrac{pV}{T}=\text{vakio}\). (+1p)
\(\begin{align} \dfrac{p_1V_1}{T_1}&=\dfrac{p_2V_2}{T_2} \quad &&|| \cdot T_1T_2\\ p_1V_1 T_2 &=p_2 V_2 T_1 \quad &&||:p_2T_1 \\ \dfrac{p_1 V_1 T_2}{p_2T_1}&=V_2 \end{align}\) (+2p)
Sijoitetaan tunnetut lukuarvot.
\(V_2 = \dfrac{98 \ 000 \text{ Pa} \cdot 2,3 \text{ l} \cdot 273,15 \text{ K}}{101 \ 325 \text{ Pa} \cdot 295,15 \text{ K}} \\ V_2 \approx 2,059 \text{ l}\) (+2p)
Vastaus: Ilmapallon tilavuus on noin 2,1 litraa. (+1p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
