a) Määrittele seuraavat käsitteet
- lämpökapasiteetti (1p)
- ominaislämpökapasiteetti (1p)
b) Kappaletta lämmitettiin 5,0 W teholla 3,0 minuuttia, jolloin sen lämpötila kasvoi 15 astetta.
Mikä on kappaleen lämpökapasiteetti, kun lämpövuodot ympäristöön oletetaan vähäisiksi? (+4p)
Ratkaisut a-kohtaan
Lämpökapasiteetti C kuvaa miten paljon kappaleeseen sitoutuu tai miten paljon kappaleesta vapautuu energiaa yhden asteen lämpötilamuutosta kohti. (+1p)
\([C]=1 \ \dfrac{\text{J}}{\text{K}}\)
Ominaislämpökapasiteetti c kuvaa miten paljon aineeseen sitoutuu tai miten paljon kappaleesta vapautuu energiaa yhden asteen lämpötilamuutosta ja kilogrammaa kohti. (+1p)
\([c]=1\ \dfrac{\text{J}}{\text{kg} \cdot \text{ K}}\)
Ratkaisu b-kohtaan
Kirjataan lähtöarvot
\(P=5,0 \text{ W}, \ t=180 \text{ s}, \Delta T=15 \text{ K}\)
Oletetaan, että lämpövuodot ympäristöön ovat vähäisiä.
Nyt lämmityksessä tehty työ on yhtä suuri, kuin kappaleen vastaanottama lämpöenergia. (+1p)
\(\begin{align} W&=Q &&||W=Pt\\ Pt&=C\Delta T \quad &&||:\Delta T \\ \dfrac{Pt}{\Delta T}&=C \end{align}\) (+2p)
Sijoitetaan tunnetut lukuarvot.
\(C=\dfrac{5,0 \text{ W} \cdot 180 \text{ s}}{15 \text{ K}} \\ C= 60 \dfrac{\text{J}}{\text{K}}\) (+1p)
Vastaus: 60 J/K.
lähde: Ylioppilastutkintolautakunta
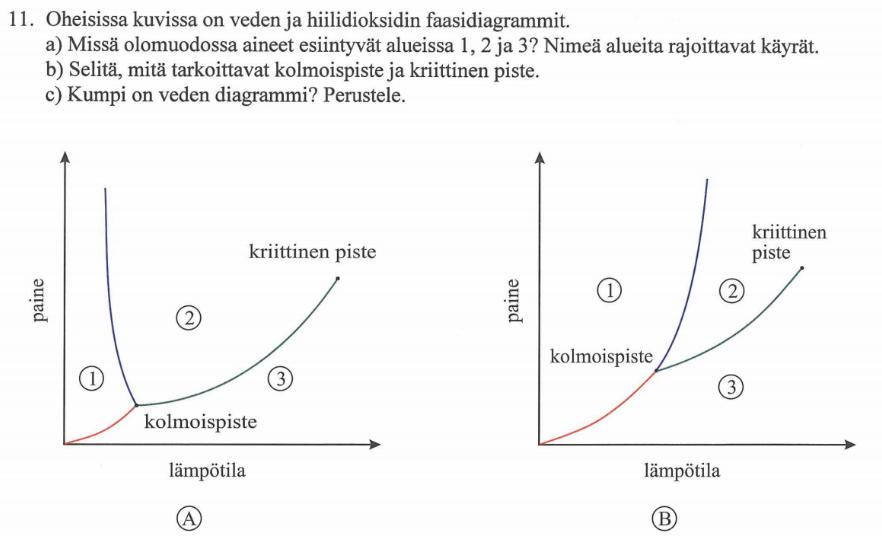
Ratkaisu a-kohtaan
1 Kiinteä, 2 Neste, 3 Kaasu (+1p)
Sublimoitumiskäyrä, Sulamiskäyrä, Höyrystymiskäyrä (+1p)
Ratkaisu b-kohtaan
Kolmoispisteen paineessa ja lämpötilassa aine esiintyy kiinteänä, nesteenä ja kaasuna. (+1p)
Kaikki kolme olomuotoa ovat tasapainossa.
Kriittistä pistettä korkeammassa lämpötilassa aine ei nesteydy painetta kasvattamalla. (+1p)
Ratkaisu c-kohtaan
Diagrammi A on veden faasidiagrammi. (+1p)
Vedelle on ominaista, että sulamispiste laskee paineen kasvaessa. (+1p)
a) Jääpalan massa on 200 g ja sen lämpötila on -15 celsiusastetta. Kuinka paljon energiaa tarvitaan jääpalan sulattamiseen? (2p)
b) Edellisen kohdan jääpala laitettiin vesikannuun, jossa oli 1,5 l vettä +12 celsiusasteen lämpötilassa. Mihin lämpötilaan vesi jäähtyy? (4p)

Ratkaisu a-kohtaan
Kirjataan lähtöarvot.
\(s=333 \text{ kJ/kg}, \ c_j=2,09 \dfrac{\text{kJ}}{\text{kg} \cdot \text{ K}}\)
\(\Delta T_{\text{j}}=15 \text{ K}, \ m=0,200 \text{ kg}\)
Energiaa kuluu jääpalan lämmittämiseen ja jääpalan sulattamiseen (+0,5p)
\(\begin{align} Q_{kok}&=Q_1+Q_2 \\ Q_{kok}&=c_jm\Delta T_j + sm \\ Q_{kok}&=2,09 \frac{\text{kJ}}{\text{kg} \cdot \text{K}}\cdot 0,200 \text{ kg} \cdot 15 \text{ K}+333 \frac{\text{ kJ}}{\text{ K}} \cdot 0,200 \text{ kg} \\ Q_{kok}&= 72,87\text{ kJ} \end{align}\)(+1p)
Vastaus: Energiaa tarvitaan noin 73 kJ. (+0,5p)
Ratkaisu b-kohtaan
Tarkastellaan vesikannussa olevan veden ja sinne laitettujen jääpalojen muodostamaa systeemiä eristettynä. (+0,5p)
Tapa 1.
Kirjataan lähtöarvot
\(c_v=4,19 \frac{\text{kJ}}{\text{kg} \cdot \text{K}}, \ m_v=1,5 \text{ kg}, \Delta T_{v}=12 \ \text{K}, \ {Q_j}=72,87 \text{ kJ}, \ c_j=2,09 \frac{\text{kJ}}{\text{kg} \cdot \text{K}}\)
Lasketaan kuinka paljon vesikannussa oleva vesi kykenee luovuttamaan lämpöenergiaa, kun se jäähtyy sulamispisteeseen.
\(Q_\text{1}=c m_v\Delta T_v \\ Q_\text{1}= 4,19 \dfrac{\text{kJ}}{\text{kg} \cdot \text{K}} \cdot 1,5 \text{ kg} \cdot 12 \text{ K} \\ Q_\text{1} = 75,42 \text{ kJ}\)
Jääpalan lämmittämiseen ja sulattamiseen kuluu a-kohdan perusteella 72,87 kJ, joten kaikki jää sulaa.
Vaihe 1. Vesikannussa oleva vesi jäähtyy, kun jää lämpenee ja sulaa.
Lasketaan vesikannussa olevan veden lämpötila, kun jääpala on lämmennyt ja sulanut kokonaan.
\(\begin{align} c_vm_v\Delta t&=Q_j \\ \Delta t&=\dfrac{Q_j}{c_vm_v} \qquad \qquad \qquad \qquad ||\text{ a-kohdasta }Q_j=72,87 \text{ kJ}\\ \Delta t&=\dfrac{72,87 \text{ kJ}}{4,19 \frac{\text{kJ}}{\text{kg} \cdot ^\circ\text{C}}\cdot 1,50\text{ kg}} \\ \Delta t&\approx 11,594 \ ^\circ\text{C} \end{align} \) (+1p)
Vesi jäähtyy lämpötilaan \(t_1=12\ ^\circ\text{C}-11,594\ ^\circ\text{C}=0,406 \ ^\circ \text{C}\)
Vaihe 2. Vesikannussa oleva vesi jatkaa jäähtymistään, kun sulanut jää lämpenee.
Jäähtyneen veden luovuttama energia on yhtä suuri kuin sulaneen jään vastaanottama energia.
\(\begin{align}Q_2&=Q_3 \\ c_vm_j\Delta t_1&=c_vm_v\Delta t_2 \\ c_vm_j(t_\text{loppu}-0\ ^\circ \text{C})&=c_vm_v(t_1-t_\text{loppu})\\ c_vm_jt_\text{loppu}&=c_vm_vt_1-c_vm_vt_\text{loppu} \\ c_vm_jt_\text{loppu}+c_vm_vt_\text{loppu}&=c_vm_vt_1 \\ (c_vm_j+c_vm_v)t_\text{loppu}&=c_vm_vt_1 \\ t_\text{loppu}&=\dfrac{c_vm_v}{c_vm_j+c_vm_v} \cdot t_1 \\ t_\text{loppu}&=\dfrac{m_v}{m_j+m_v}\cdot t_1\end{align} \) (+1p)
Sijoitetaan lukuarvot.
\(t_\text{loppu}=\dfrac{m_v}{m_j+m_v}\cdot t_1 \\ t_\text{loppu}=\dfrac{1,50 \text{ kg}}{0,200 \text{ kg} + 1,50 \text{ kg}} \cdot 0,406\ ^\circ \text{C} \\ t_\text{loppu} \approx 0,358 \ ^\circ \text{C}\) (+1p)
Vastaus: Vesikannun ja jään muodostaman systeemin loppulämpötila on noin 0,36 celsiusastetta. (+0,5p)
Tapa 2.
Kirjataan lähtöarvot
\(c_j=2090 \frac{\text{J}}{\text{kg}\cdot ^\circ\text{C}}, \ m_j=0,200\text{ kg}, \ \Delta T_j=15 \text{ K}\)
\(c_v=4190 \frac{\text{J}}{\text{kg}\cdot ^\circ\text{C}}, \ m_v=1,50\text{ kg}, \ T_{v0}=12^\circ \text{C}\)
Jääpalan vastaanottama energia on yhtä suuri kuin veden luovuttama energia. (+0,5p)
\(\begin{align} Q_\text{vastaanotettu}&=Q_\text{luovutettu} \\ c_jm_j\Delta T_j + sm+c_vm_j(T_\text{loppu}-0^\circ\text{ C})&=c_vm_v(T_{v0}-T_\text{loppu}) \\ c_jm_j\Delta T_j + sm_j+c_vm_jT_\text{loppu}&=c_vm_vT_{v0}-c_vm_vT_\text{loppu} \\ c_vm_jT_\text{loppu}+c_vm_vT_\text{loppu}&=c_vm_vT_{v0}-sm_j-c_jm_j\Delta T_j \\ (c_vm_j+c_vm_v)T_\text{loppu}&=c_vm_vT_{v0}-sm_j-c_jm_j\Delta T_j \\ T_\text{loppu}&=\dfrac{c_vm_vT_{v0}-sm_j-c_jm_j\Delta T_j}{c_vm_j+c_vm_v}\\ T_\text{loppu}&=\dfrac{c_vm_vT_{v0}-sm_j-c_jm_j\Delta T_j}{c_v(m_j+m_v)}\\ T_\text{loppu}&=\dfrac{4190 \frac{\text{J}}{\text{kg} \cdot \text{ K}} \cdot 1,50 \text{ kg} \cdot 12 \text{ K}-333 \ 000 \frac{\text{J}}{\text{ kg}} \cdot 0,200 \text{ kg}-2090 \frac{\text{J}}{\text{kg}}\cdot 0,200 \text{ kg}\cdot 15 \text{ K}}{4190 \frac{\text{J}}{\text{kg} \cdot \text{ K}}(0,200 \text{ kg} + 1,50 \text{ kg})} \\ T_\text{loppu}&\approx 0,36^\circ \text{C} \end{align} \) (+3p)
Vastaus: Veden ja sulaneen jään muodostaman systeemin loppulämpötila on 0,36 celsiusastetta. (+0,5p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
