Piirrä vihkoosi koordinaatisto ja merkitse siihen pisteet
$A=(-2,4)$
$B=(3,-2)$
$C=(-6,0)$
$D=(-4,3)$
$E=(0,0)$
$F=(5,1)$
Harjoittele myös, miten pisteet merkitään koordinaatistoon GeoGebran avulla syöttämällä syöttökenttään seuraavat komennot:
- A=(-2,4) tai pelkästään (-2,4)
- B=(3,-2)
- jne...
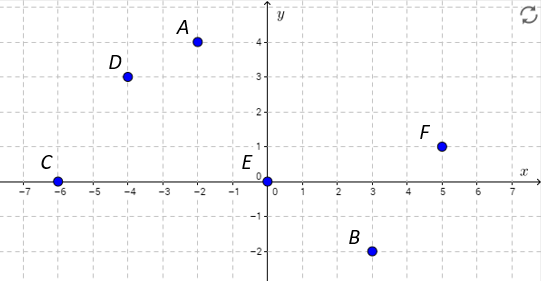
Jokaisesta oikeaan kohtaan koordinaatistoon piirretystä pisteestä (+1p.)
Piirrä vihkoosi samaan koordinaatistoon suoran $y=2x+3$ ja funktion $f(x)=-x+1$ kuvaajat.
Harjoittele myös suoran ja funktion kuvaajan piirtämistä alla olevan GeoGebran avulla syöttämällä syöttökenttään seuraavat komennot:
- y=2x+3
- f(x)=-x+1
Suoran yhtälön ja funktion kuvaajat piirretään esimerkiksi etsimällä muutamia koordinaattipisteiden arvoja, jotka toteuttavat kyseiset yhtälöt.
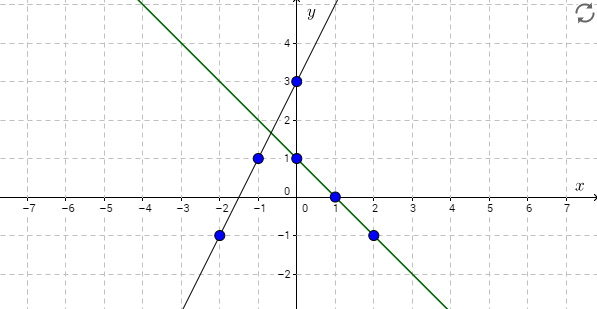
Koska sekä suoran yhtälö että funktion lauseke ovat ensimmäistä astetta, molempien kuvaaja on suora. Tällöin piirtämiseen tarvitaan vähintään kaksi koordinaattipistettä. (+1p)
Etsitään pisteet esim. taulukoimalla
\(\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|} \hline x & y=2x+3 & \begin{array}{c}\text{Koordinaatti-} \\ \text{piste} \end{array} \T \\ \hline -2 & y=2\cdot(-2)+3=-1 \phantom{\Big|} & (-2,-1) \\ \hline -1 & y=2\cdot(-1)+3=1 \phantom{\Big|} & (-1,1) \\ \hline 0 & y=2\cdot0+3=3 \phantom{\Big|} & (0,3) \\ \hline \end{array}\) (+1p)
\(\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|} \hline x & f(x)=-x+1 & \begin{array}{c}\text{Koordinaatti-} \\ \text{piste} \end{array} \T \\ \hline 0 & f(0)=-0+1=1 \phantom{\Big|} & (0,1) \\ \hline 1 & f(1)=-1+1=0 \phantom{\Big|} & (1,0) \\ \hline 2 & f(2)=-2+1=-1 \phantom{\Big|} & (2,-1) \\ \hline \end{array}\) (+1p)
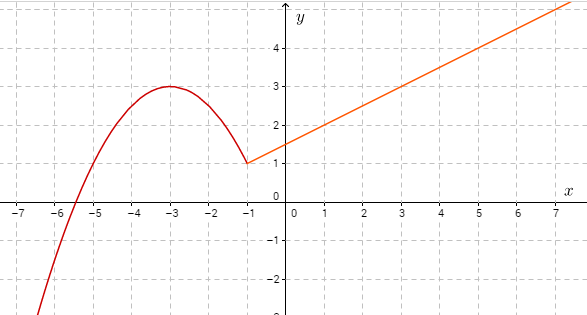
Alla on erään funktion $f(x)$ kuvaaja. Määritä kuvaajan avulla
a) $f(0)$
b) $f(x)=0$
c) $f(x)=1$
d) $f(1)$
e) $f(5)$
f) $f(x)=-2$
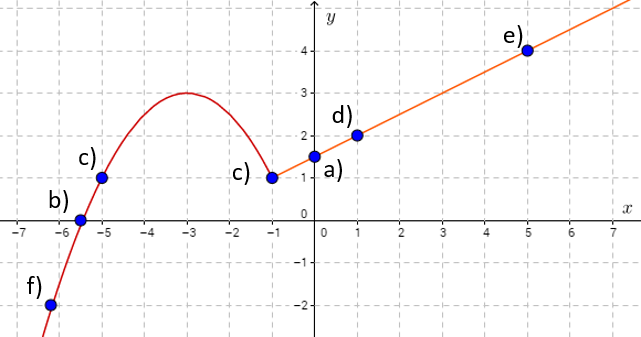
Kuvaajasta voidaan havaita, että
a) \(f(0)\approx\underline{\underline{1,5}}\). (+1p)
b) $f(x)=0$, kun \(\underline{\underline{x\approx-5,5}}\). (+1p)
c) $f(x)=1$, kun \(\underline{\underline{x\approx-5}}\) ja \(\underline{\underline{x\approx-1}}\). (+1p)
d) \(f(1)\approx\underline{\underline{\ 2\ }}\). (+1p)
e) \(f(5)\approx\underline{\underline{\ 4\ }}\). (+1p)
f) $f(x)=-2$, kun \(\underline{\underline{x\approx-6,2}}\). (+1p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
