Käyräparven $y=ax^2+(1-4a)x+3a$, missä $a\in\mathbb{R}$, kaikki käyrät leikkaavat kahdessa kiinteässä pisteessä. Mitkä nämä pisteet ovat?
Valitaan ensin käyräparvesta kaksi käyrää antamalla parametrille $a$ kaksi eri arvoa. Näiden käyrien yhteiset pisteet ovat ainoita mahdollisia koko käyräparven yhteisiä pisteitä.
$a=0:\quad y=x;$
$a=1:\quad y=x^2-3x+3$. (+1p)
Ratkaistaan näiden kahden käyrän yhteiset pisteet yhtälöparilla
\(\begin{cases} y=x\\ y=x^2-3x+3 \end{cases}\) (+1p)
Tästä saadaan sijoittamalla ylempi yhtälö alempaan yhtälö
$x=x^2-3x+3,$
jonka juuret ovat $x=1$ ja $x=3$. (+1p)
Yhtälöparin ratkaisuina ovat siis pisteet $(1,1)$ ja $(3,3)$. (+1p)
Sijoitetaan nämä pisteet vielä alkuperäiseen käyräparven yhtälöön:
\(\begin{align} y&=ax^2+(1-4a)x+3a \quad || x=1, y=1\\ 1&=a+1-4a+3a\\ 0&=0\quad \mbox{aina tosi} \end{align}\)(+1p)
\(\begin{align} y&=ax^2+(1-4a)x+3a \quad || x=3, y=3\\ 3&=9a+3-12a+3a\\ 0&=0\quad \mbox{aina tosi} \end{align}\)
Näin ollen koko käyräparvelle yhteisiä pisteitä ovat $(1,1)$ ja $(3,3)$. (+1p)
Tutki piirtämällä, montako yhteistä tangenttia on ympyröillä $x^2+y^2=1$ ja $x^2+(y-6)^2=4$. Määritä yhteisten tangenttien yhtälöt.
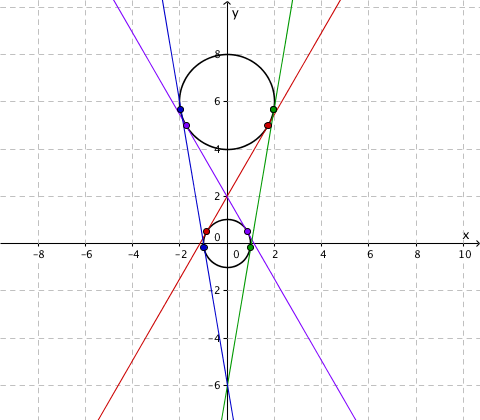
Yhteisiä tangentteja on neljä. (+1p)
Olkoon tangentin yhtälö $y=kx+b$. Nyt tällä tangentilla on yksi yhteinen piste ympyrän $x^2+y^2=1$ kanssa, eli yhtälöparilla
\(\begin{cases} x^2+y^2=1\\ y=kx+b \end{cases}\)
on täsmälleen yksi ratkaisu. (+1p)
Tästä saadaan sijoittamalla alempi yhtälö ylempään $x^2+(kx+b)^2=1$, eli $(k^2+1)x^2+2kbx+(b^2-1)=0$, jolla on yksi ratkaisu täsmälleen silloin, kun sen diskriminantti on nolla, eli kun
$(2kb)^2-4(k^2+1)(b^2-1)=0.$ Tämä yhtälö voidaan sieventää muotoon $k^2=b^2-1.$ (+1p)
Vastaavasti tangetilla $y=kx+b$ on täsmälleen yksi yhteinen piste ympyrän $x^2+(y-6)^2=4$ kanssa, minkä vuoksi yhtälöparilla
\(\begin{cases} x^2+(y-6)^2=4\\ y=kx+b \end{cases}\)
on myös oltava täsmälleen yksi ratkaisu. Vastaava sijoitus ylempään yhtälöön tuottaa nyt yhtälön $x^2+(kx+(b-6))^2=4$, eli $(k^2+1)x^2+2k(b-6)x+((b-6)^2-4)=0$, jolla on yksi ratkaisu silloin, kun
$(2k(b-6))^2-4(k^2+1)((b-6)^2-4)=0$. Tämä yhtälö sievenee vielä muotoon $4k^2-b^2+12b-32=0$ (+1p)
Olemme saaneet siis yhtälöparin
\(\begin{cases} k^2=b^2-1\\ 4k^2-b^2+12b-32=0\end{cases}\)
josta laskimella saadaan ratkaisulukuparit $k=\pm \sqrt{35}$, $b=-6$ ja $k=\pm\sqrt{3}$, $b=2$. Siis ratkaisutangentit ovat $y=\pm\sqrt{35}x-6$ ja $y=\pm\sqrt{3}x+2$. (+2p)
(Tehtävässä voi hyödyntää myös tavallista tasogeometriaa seuraavasti: Tangentit sijaitsevat symmetrisesti ympyröiden eri puolilla. Tangenttipisteet ovat ympyröiden keskipisteiden kautta kulkevalla suoralla. Yhdenmuotoisten kolmioiden avulla voidaan osoittaa, että ympyröiden välissä oleva tangenttipiste jakaa keskipisteiden yhdysjanan ympyröiden säteiden suhteessa. Samoin tekee janan ulkopuolisesti pienemmän ympyrän takana oleva tangettipiste. Näin saadaan ratkaistuksi vakion $b$ arvot $b=2$ ja $b=-6$. Kulmakertoimet voidaan sitten ratkaista analyyttisen geometrian menetelmin.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
