Paraabeli on määritelmänsä mukaan niiden pisteiden joukko, jotka ovat yhtä kaukana annetusta pisteestä (polttopiste) ja annetusta suorasta (johtosuora). Määritä yhtälö paraabelille, jonka polttopiste on $P(2,3)$ ja johtosuora $y=-2x+1$.
Tutki tehtävää myös Geogebran avulla käyttäen seuraavia komentoja syöttökentässä (paina jokaisen komennon jälkeen ENTER):
- a:y=–2x+1 [tämä luo suoran, jonka nimi on a]
- P=(2,3) [tämä luo pisteen P]
- Paraabeli[P,a]
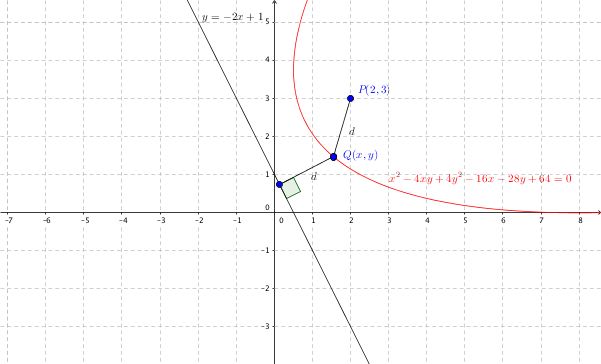
Olkoon $Q(x,y)$ mielivaltainen kysytyn paraabelin piste. Sen etäisyys pisteestä $P(2,3)$ on
$d=\sqrt{(x-2)^2+(y-3)^2}.$ (+1p)
Muunnetaan suora $y=-2x+1$ normaalimuotoon $2x+y-1=0$. Pisteen $Q(x,y)$ etäisyys tästä suorasta on
$d=\displaystyle\frac{|2x+y-1|}{\sqrt{2^2+1^2}}.$ (+1p)
Nämä etäisyydet ovat samat, joten saadaan yhtälö
$\displaystyle\sqrt{(x-2)^2+(y-3)^2} =\frac{|2x+y-1|}{\sqrt{2^2+1^2}}.$ (+2p)
Puolittain neliöimällä ja lausekkeet auki kertomalla saadaan paraabelin yhtälö sievennettyä muotoon
\(\begin{align} (x-2)^2+(y-3)^2 &=\frac{(2x+y-1)^2}{5} \\ 5(x^2-4x+4+y^2-6y+9)&=4x^2+y^2+4xy-4x-2y+1\\ x^2-4xy+4y^2-16x-28y+64&=0. \quad \color{red}{\mbox{(+2p)}}\end{align}\)
Mistä pisteistä ympyrä $x^2+y^2-2y=0$ näkyy suorassa kulmassa?
Voit tutkia tehtävää oheisen Geogebra-appletin avulla. Syötä ympyrän yhtälö muodossa x^2+y^2-2y=0 syöttökenttään. Sen jälkeen voit työkalupalkin työkalujen avulla luoda pisteitä ja tangentteja sekä laskea tangenttien välisiä kulmia.
Muokataan ensin ympyrän yhtälöä:
\(\begin{align} x^2+y^2-2y&=0\\ x^2+y^2-2\cdot y\cdot 1+1&=1\\ x^2+(y-1)^2&=1^2 \end{align}\)
Ympyrän keskipiste on siis $(0,1)$ ja säde $1$. (+2p)
Piirretään ympyrälle tangentit, jotka ovat toisiaan vastaan kohtisuorassa:
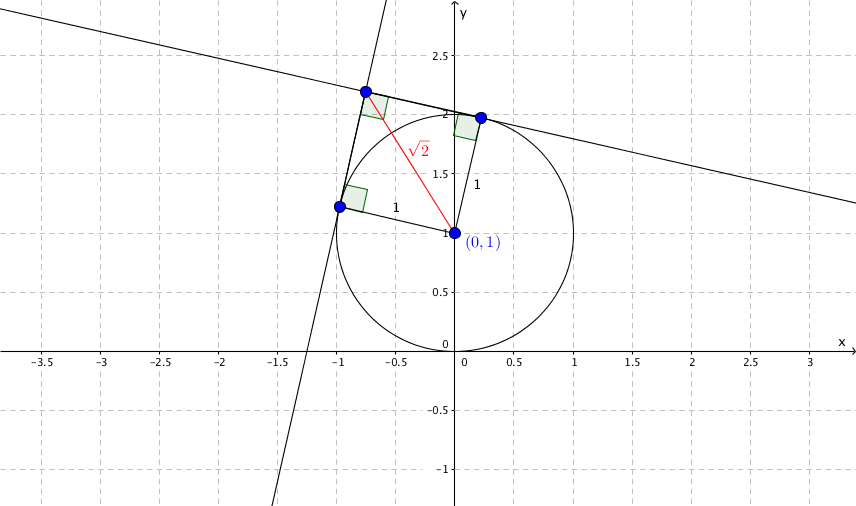
Koska tangentti ja sivuamispisteeseen piirretty säde ovat kohtisuorassa, muodostuu säteistä sekä sivuamispisteiden ja tangenttipisteen välisistä janoista välttämättä neliö, jonka sivun pituus on $1$, joten sen lävistäjän pituus on $\sqrt{2}$. (+2p)
Ympyrän symmetrian vuoksi tilanne on samanlainen riippumatta siitä, mistä suoran kulman tuottavasta tangenttipisteestä on kyse. Siispä ratkaisukäyrä on ympyrä, jonka keskipiste on $(0,1)$ ja säde $\sqrt{2}$. (+1p)
Tämän käyrän yhtälö on $x^2+(y-1)^2=2$. (+1p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
