a) Ratkaise yhtälö \(x^4=16\).
b) Ratkaise yhtälö \(x^5=-32\).
c) Ratkaise yhtälö \(3x^6=15\).
Tutki alla olevien liukukytkimien avulla funktion $f(x)=x^n$ kuvaajan muotoa eksponentin $n$ eri lukuarvoilla ja ratkaise alla olevat tehtävät kuvaajan avulla.
d) Määritä graafisesti $f(-1)$, kun $f(x)=x^6$.
e) Ratkaise graafisesti yhtälö $x^4=3$.
f) Ratkaise graafisesti yhtälö $x^5=-2$.
\( \require{color} \begin{align*} \textbf{a)}\ x^4&=16\\ x&=\pm\sqrt[4]{16}\\ x&= \pm 2 \end{align*}\)
Vastaus: \(x=2\) tai \(x=-2\). \(\require{color}\color{red}{\text{(+1p)}}\)
\( \require{color} \begin{align*} \textbf{b)}\ x^5&=-32\\ x&=\sqrt[5]{-32}\\ x&= -2 \end{align*}\)
Vastaus: \(x=-2\). \(\require{color}\color{red}{\text{(+1p)}}\)
\( \require{color} \begin{align*} \textbf{c)}\ 3x^6&=15 \quad || :3 \\ \ x^6&=5 \\ x&=\pm \sqrt[6]{5} \approx\pm1,31 \end{align*}\)
Vastaus: \(x=\sqrt[6]{5}\approx1,31\) tai \(x=-\sqrt[6]{5}\approx-1,31\). \(\require{color}\color{red}{\text{(+1p)}}\)
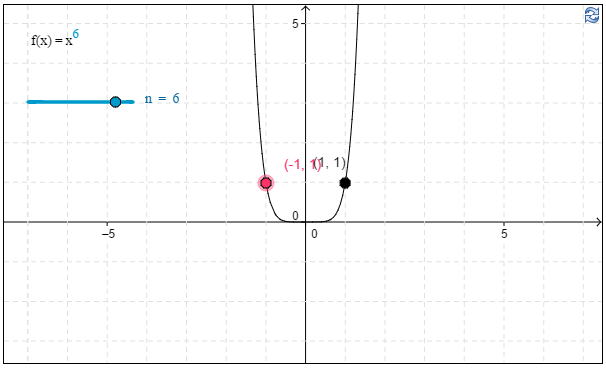
d) Kuvaajan avulla havaitaan, että \(f(-1)=\underline{\underline{\ 1\ }}\). \(\require{color}\color{red}{\text{(+1p)}}\)
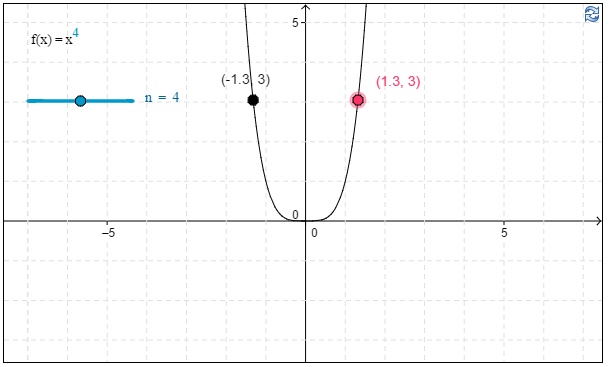
e) Kuvaajan avulla havaitaan, että yhtälön $x^4=3$ ratkaisut ovat \(x\approx\underline{\underline{-1,3}}\) ja \(x\approx\underline{\underline{1,3}}\). \(\require{color}\color{red}{\text{(+1p)}}\)
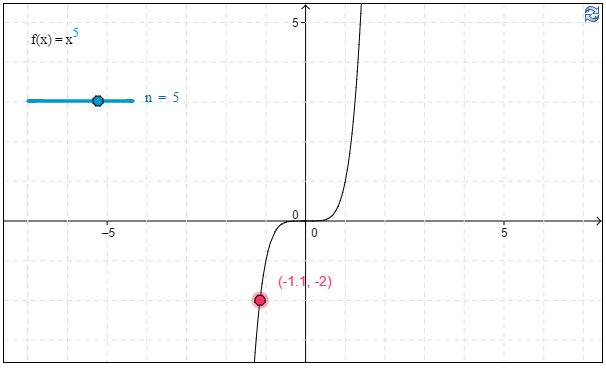
f) Kuvaajan avulla havaitaan, että yhtälön $x^5=-2$ ratkaisu on \(x\approx\underline{\underline{-1,1}}\). \(\require{color}\color{red}{\text{(+1p)}}\)
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Tutki alla olevien liukukytkimien avulla funktion $f(x)=a^x$ kuvaajan muotoa kantaluvun $a$ eri lukuarvoilla (kun $a>0$).
a) Kuvaile sanallisesti, miten kantaluvun $a$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon.
b) Määritä graafisesti (liikuttamalla punaista pistettä käyrällä) funktion $f(x)=2^x$ arvo kohdassa $x=2$.
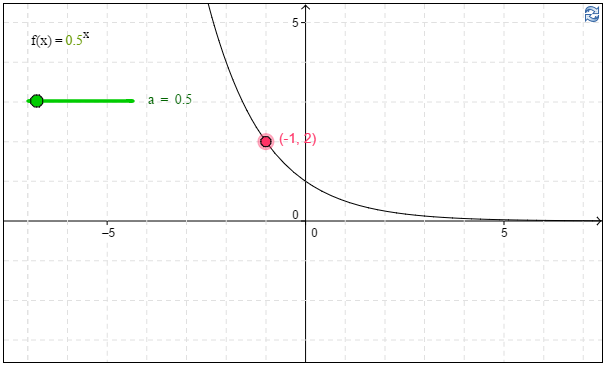
c) Määritä graafisesti $f(-1)$, kun $f(x)=0,\!5^x$.
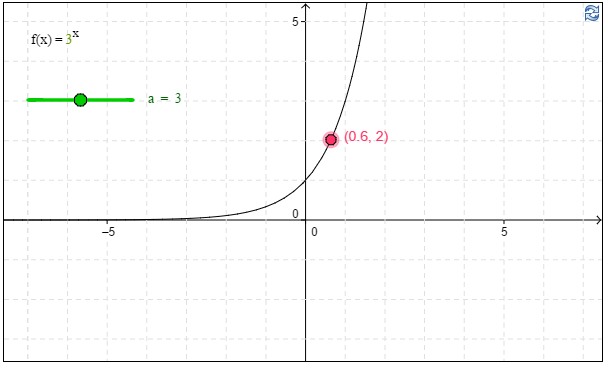
d) Ratkaise graafisesti yhtälö $3^x=2$.
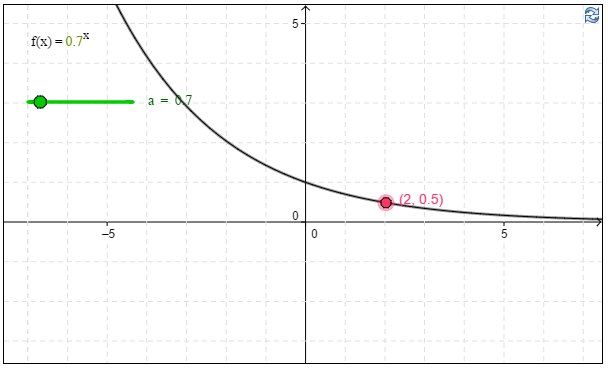
e) Ratkaise graafisesti yhtälö $0,\!7^x=0,5$.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a)
- Eksponenttifunktion kuvaaja kulkee aina pisteen $(0,1)$ kautta riippumatta kantaluvun arvosta, sillä $f(0)=a^0=1$.
- Kun $a>1$, funktion $f(x)=a^x$ arvot kasvavat muuttujan $x$ kasvaessa. \(\require{color}\color{red}{\text{(+1p)}}\)
- Kun $0<a<1$, funktion $f(x)=a^x$ arvot pienenevät muuttujan $x$ kasvaessa. \(\require{color}\color{red}{\text{(+1p)}}\)
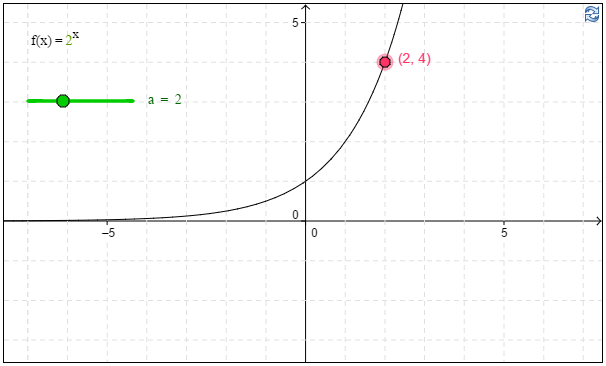
b) Kuvaajan avulla havaitaan, että funktion $f(x)=2^x$ arvo \(f(x)=\underline{\underline{\ 4\ }}\), kun $x=2$. \(\require{color}\color{red}{\text{(+1p)}}\)
c) Kuvaajan avulla havaitaan, että funktiolle $f(x)=0,\!5^x$ pätee \(f(-1)=\underline{\underline{\ 2\ }}\). \(\require{color}\color{red}{\text{(+1p)}}\)
d) Kuvaajan avulla havaitaan, että yhtälön $3^x=2$ ratkaisu on \(x\approx\underline{\underline{0,6}}\). \(\require{color}\color{red}{\text{(+1p)}}\)
e) Kuvaajan avulla havaitaan, että yhtälön $0,\!7^x=0,\!5$ ratkaisu on \(x\approx\underline{\underline{\ 2\ }}\) (hyväksytään ratkaisut väliltä $[1,\!8;2,\!2]$). \(\require{color}\color{red}{\text{(+1p)}}\)
a) Ratkaise ilman logaritmia yhtälö \(2^{x-2}=8\).
b) Ratkaise logaritmin avulla yhtälö \(3^x=10\).
c) Ratkaise yhtälö \(2\cdot5^x=50\).
\( \require{color} \begin{align*} \textbf{a)}\ 2^{x-2}&=8\\ 2^{x-2}&=2^3\\ x-2&= 3&&\color{red}\text{(+1p)}\\x&=5 \end{align*}\)
Vastaus: $x=5$. (+1p)
\( \require{color} \begin{align*} \textbf{b)}\ 3^x&=10\\ \text{lg }3^x&=\text{lg }10\\ x\cdot\text{ lg }3&= \text{lg }10&&\color{red}\text{(+1p)}\\x&=\frac{\text{lg }10}{\text{lg }3}\approx2,\!0959... \end{align*}\)
Vastaus: $x=2,\!10$. (+1p)
\( \require{color} \begin{align*} \textbf{c)}\ 2\cdot5^x&=50&&|| :2\\ 5^x&=25\\ 5^x&= 5^2&&\color{red}\text{(+1p)}\\x&=2 \end{align*}\) (tai logaritmin avulla ratkaistuna)
Vastaus: $x=2$. (+1p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
