Värähdysliike:
Ymmärrän, millaista liikettä värähdysliike on ja miten se eroaa etenevästä liikeestä.
Oppimisen tueksi:
Värähdysliike on jaksollisesti tapahtuvaa liikettä tasapainoaseman ympärillä.
Mekaaninen aaltoliike on toisiinsa kytkettyjen värähtelijöiden liikettä.
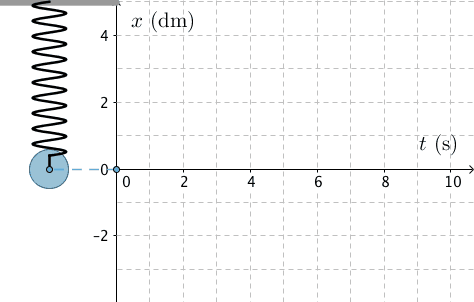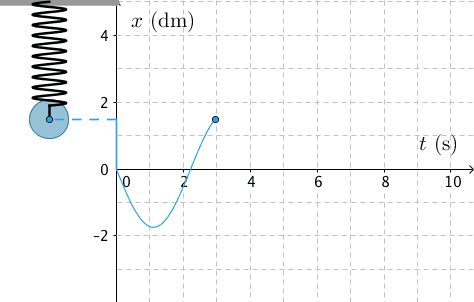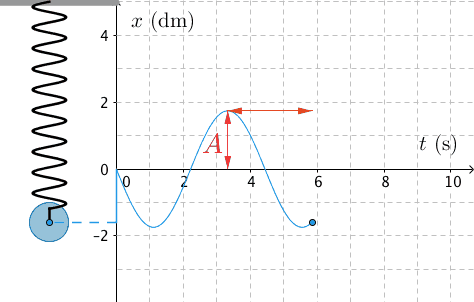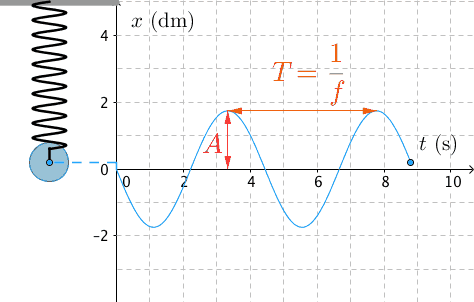
Muistiinpanot
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Aaltoliike:
Ymmärrän, mitä yhteistä ja mitä eroa on värähdysliikkeellä ja aaltoliikkeellä.
Oppimisen tueksi:

Värähdysliike on jaksollisesti tapahtuvaa liikettä tasapainoaseman ympärillä.
Mekaaninen aaltoliike on toisiinsa kytkettyjen värähtelijöiden liikettä.
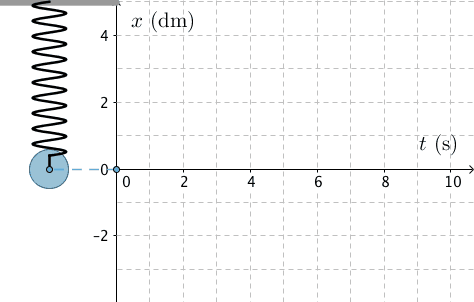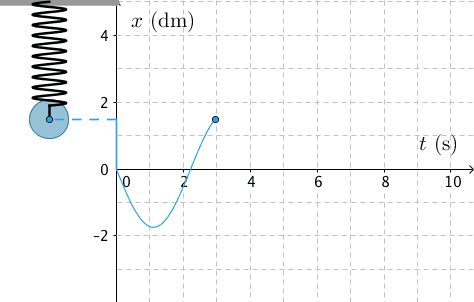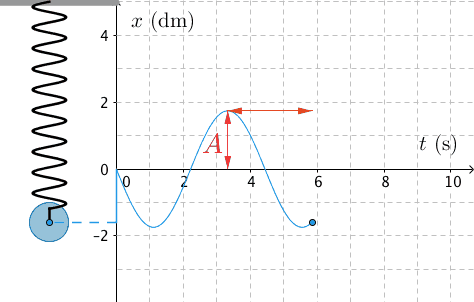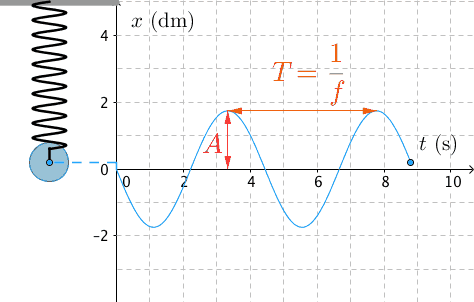
Muistiinpanot:
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Aaltoliikkeen käsitteitä:
Ymmärrän käsitteet amplitudi, taajuus, jaksonaika.
Oppimisen tueksi
Amplitudi A on aaltoliikkeen suurin poikkeama sen tasapainoasemasta.
Aallonpituus \(\lambda\) on peräkkäisten aallonharjojen (tai pohjien) välinen etäisyys.
Jaksonaika T on yhteen värähdykseen kuluva aika.
Jaksonajan käänteisarvo on taajuus \(f=\dfrac{1}{T}\) , jonka yksikkö on 1 Hz.
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Harmoninen voima:
Ymmärrän, millainen voima on harmonista voimaa. Ymmärrän myös sanan “harmoninen” merkityksen käsitteessä.
Oppimisen tueksi:
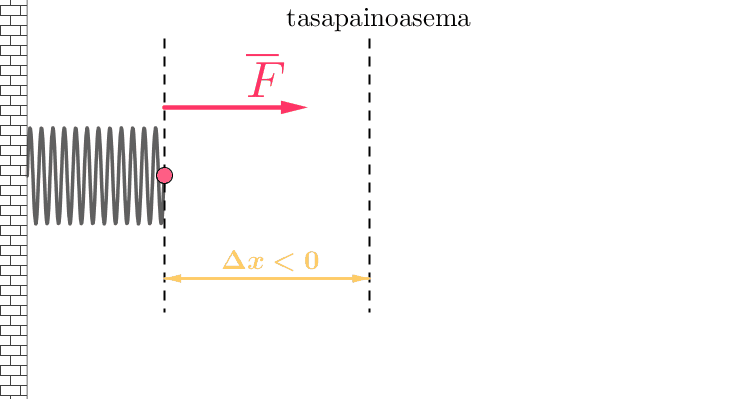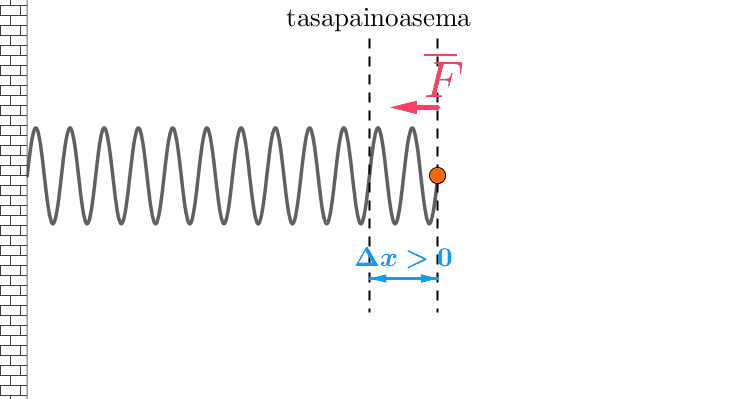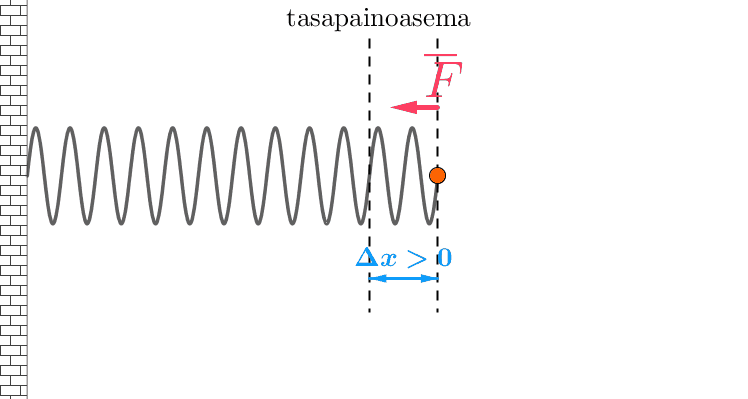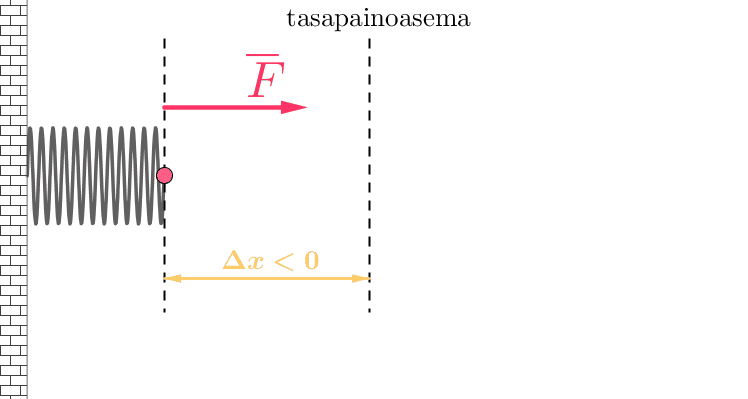
Harmoninen voima
- suoraan verrannollinen poikkeamaan tasapainoasemasta
- suunta on aina kohti tasapainoasemaa.
Harmonisen voiman suuruutta ja suuntaa kuvaa Hooken laki
\(F=-kx\),
jossa \(k\) on jousivakio ja \(x\) on poikkeama tasapainoasemasta.
Jousivoima on esimerkki harmonisesta voimasta.
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Harmonisen voiman käsitteitä:
Ymmärrän käsitteet jousivakio, jousivoima ja jaksonaika. Osaan myös määrittää kokeellisesti jousen jousivakion.
Oppimisen tueksi:
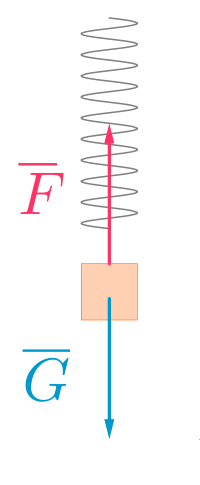
Ripustetaan punnus jouseen roikkumaan ja odotetaan, että punnus on levossa.
Punnukseen vaikuttaa ainoastaan punnuksen paino \(G\) ja jousivoima \(F\).
Tasapainotilanteessa punnus on levossa jolloin punnukseen vaikuttava kokonaisvoima on nolla.
Newtonin 2. lain mukaan
\(\begin{align} \sum \overline{F}&=0 \\ \overline{F}+\overline{G}&=0 \\ F&=G \end{align}\)
Ripustetaan jouseen erimassaisia punnuksia ja tutkitaan jousen venymää.
Punnuksen paino \(G\) on yhtä suuri kuin jousen punnukseen kohdistama jousivoima \(F\).
Sijoitetaan mittaustulokset \((x, \ F)-\)koordinaatistoon, jossa \(x\) on jousen venymä ja \(F\) on punnukseen kohdistuva jousivoima.
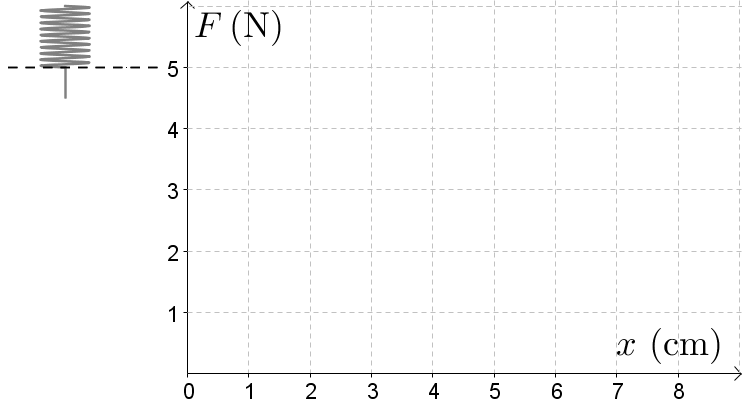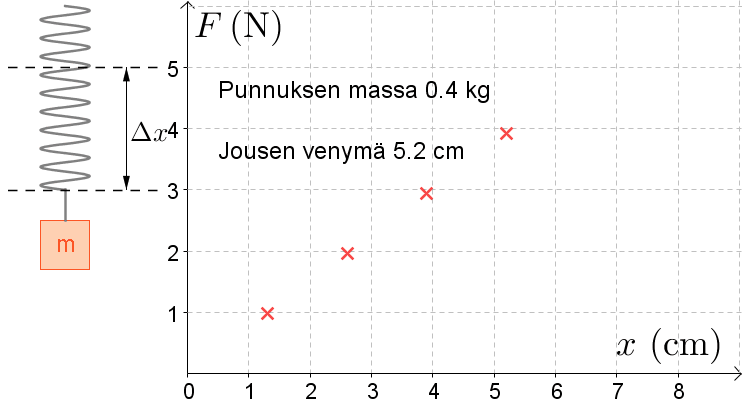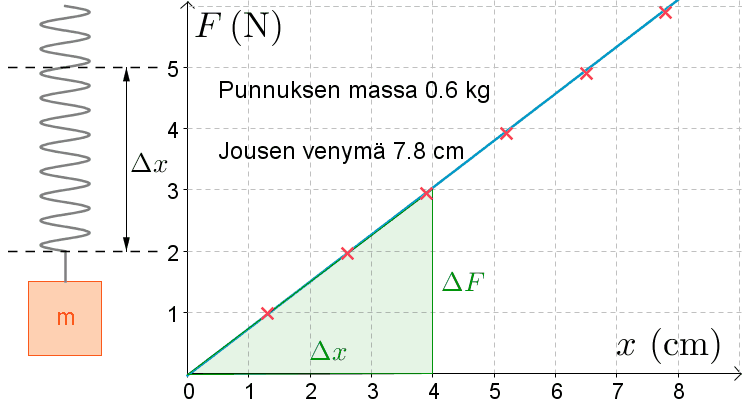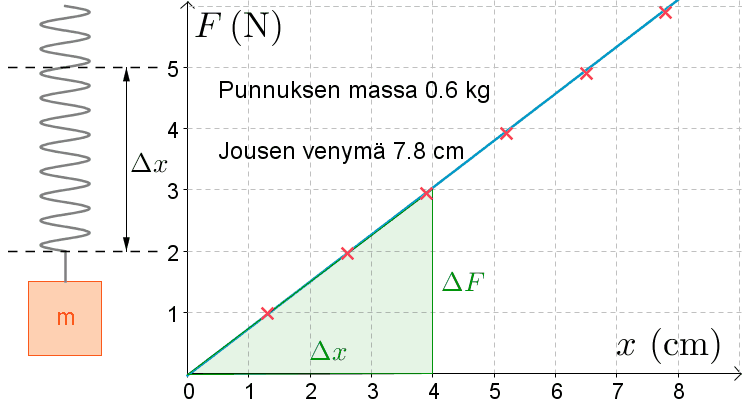
Huomataan, että jousivoima \(F\) ja jousen venymä \(x\) ovat suoraan verrannollisia eli \(F=k \cdot x\).
Ratkaistaan suoran fysikaalinen kulmakerroin.
\(k=\dfrac{\Delta F}{\Delta x}=\dfrac{3,0 \text{ N}}{0,04 \text{ m}}=75 \text{ N/m}\)
\((x, \ F)-\)koordinaatistoon piirretyn suoran fysikaalinen kulmakerroin on jousen jousivakio, joka kuvaa jousen jäykkyyttä.
Mitä suurempi jousivakion arvo on, niin sitä jäykempi jousi on.
Jousivoima on esimerkki harmonisesta voimasta.
Harmonisen voiman aiheuttamaa liikettä sanotaan harmoniseksi värähdysliikkeeksi.
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
