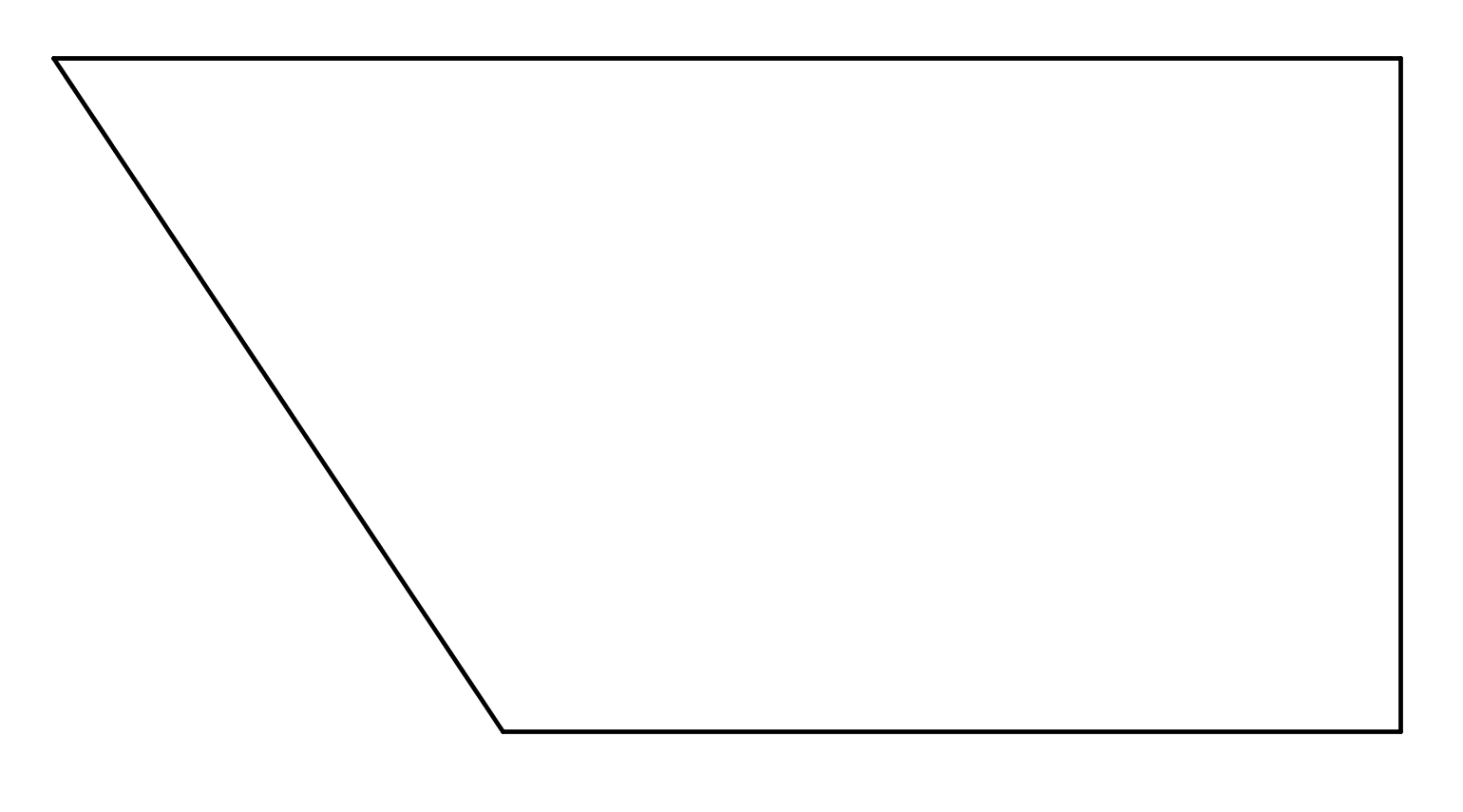
Anna monikulmiolle mahdollisimman tarkasti kuvaava nimi.
a)

b)
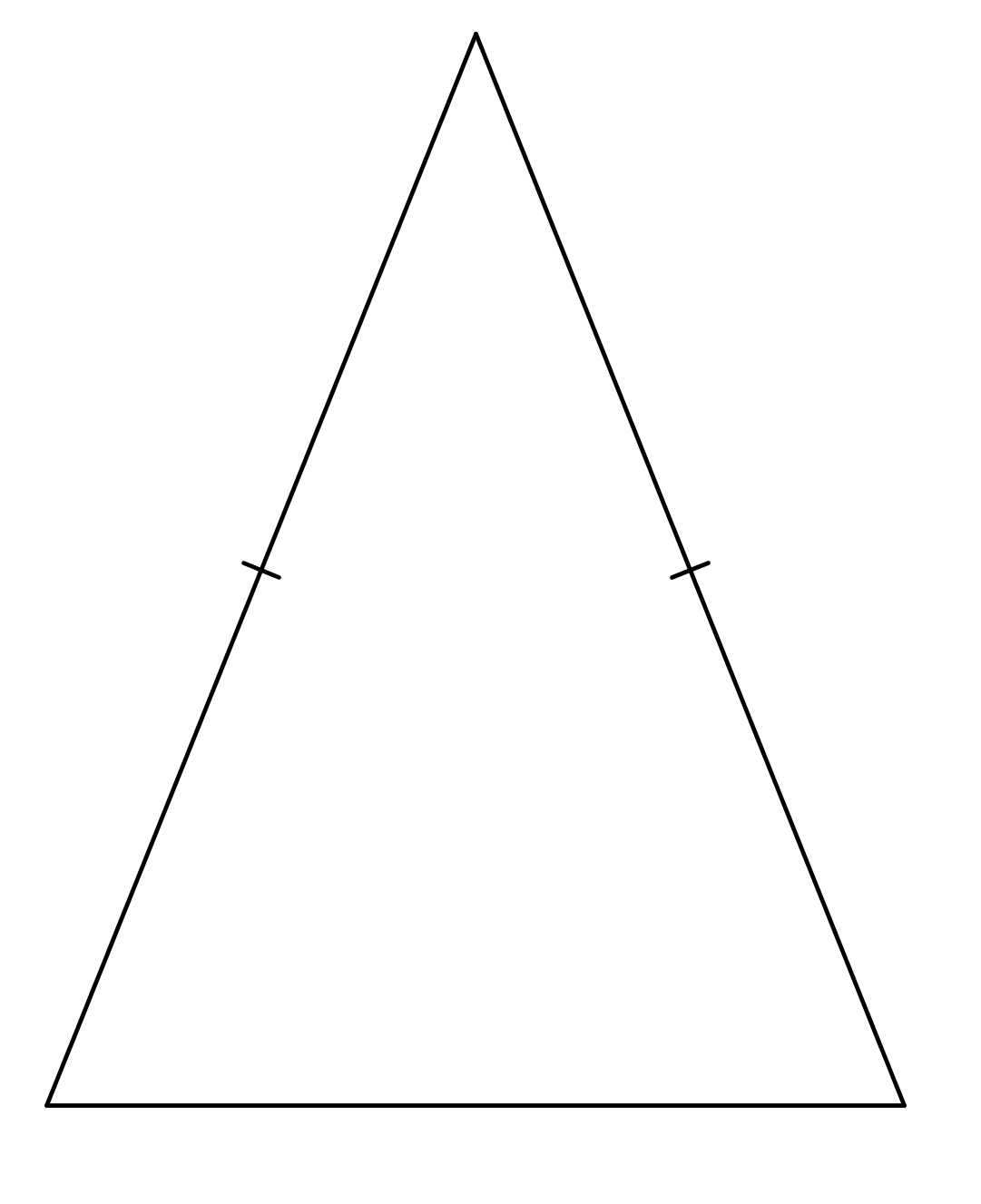
c)
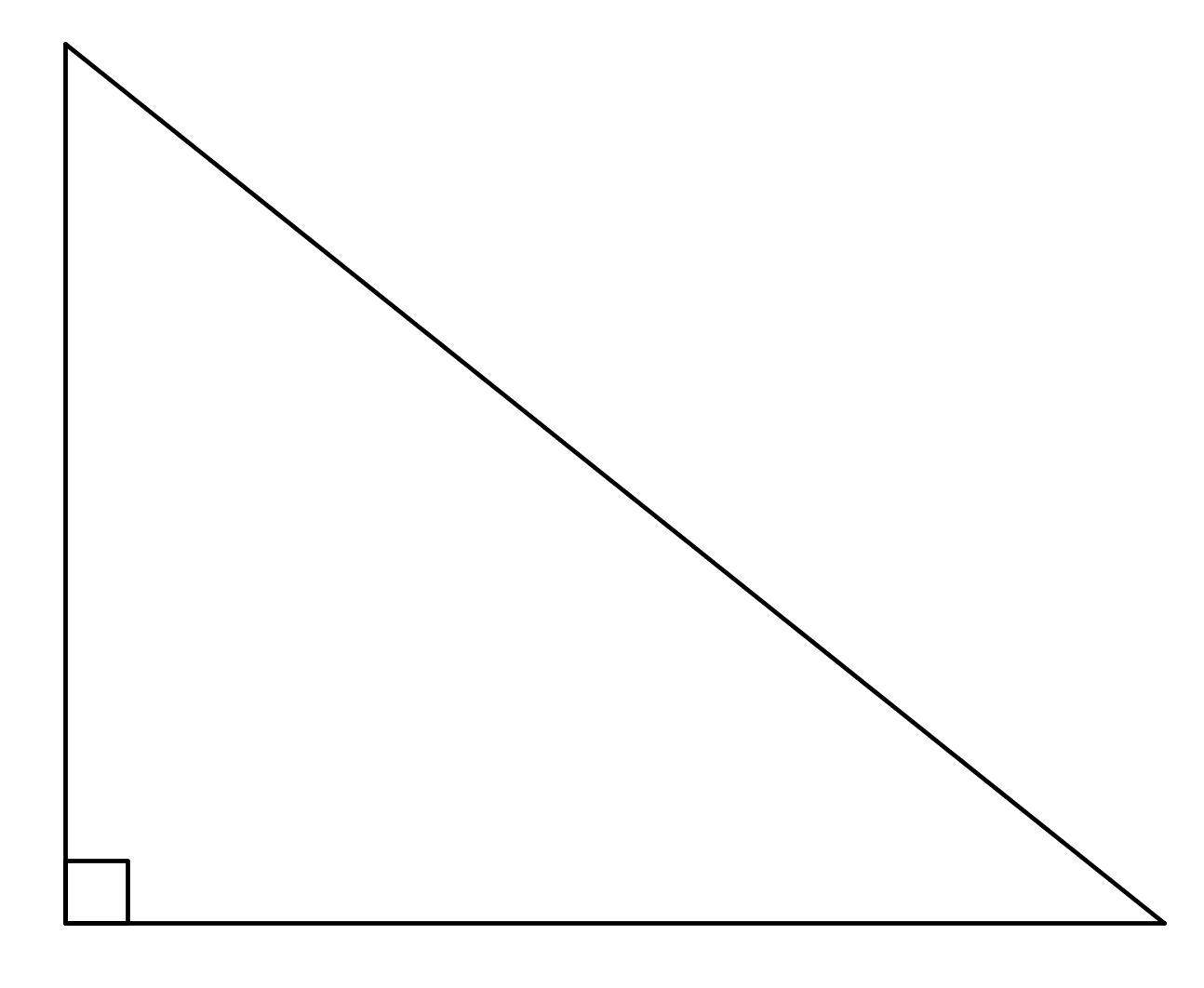
d)
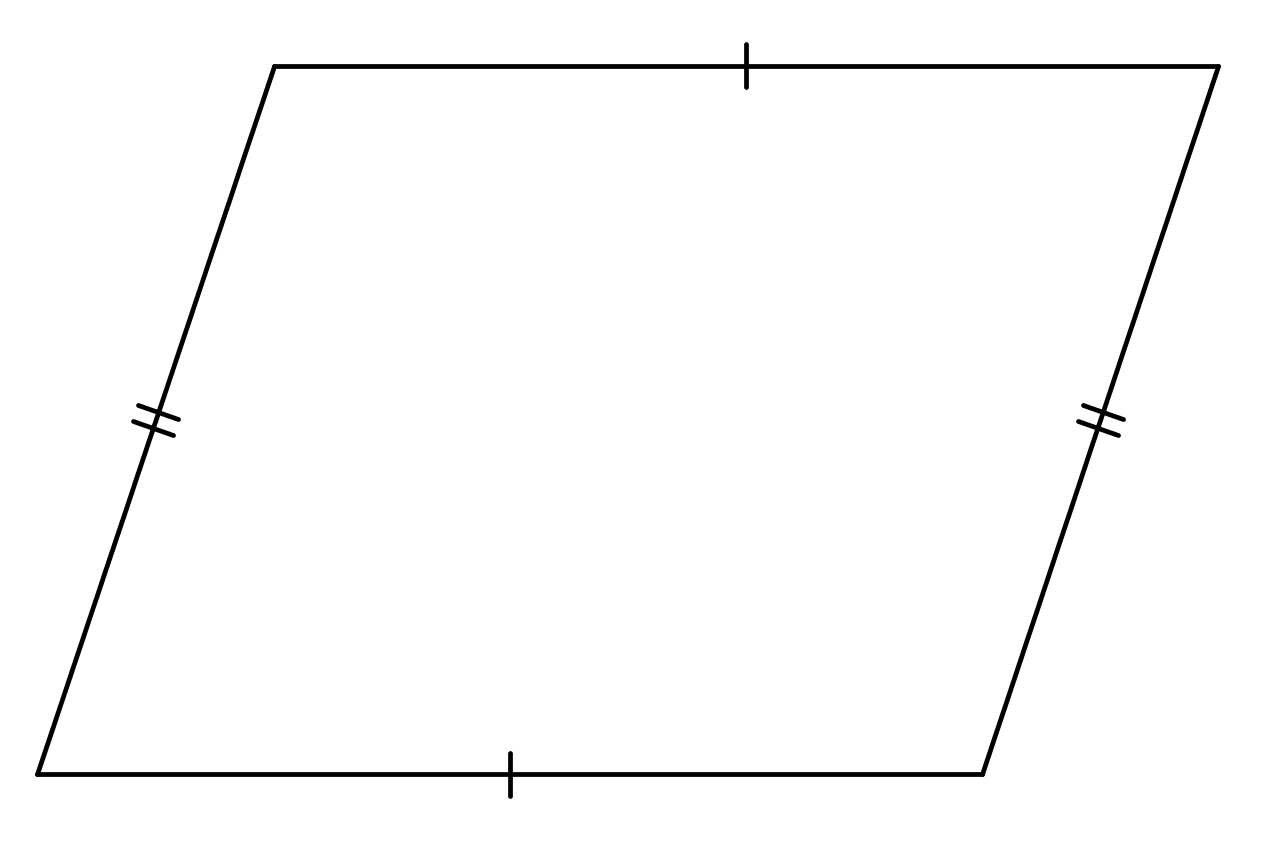
e)
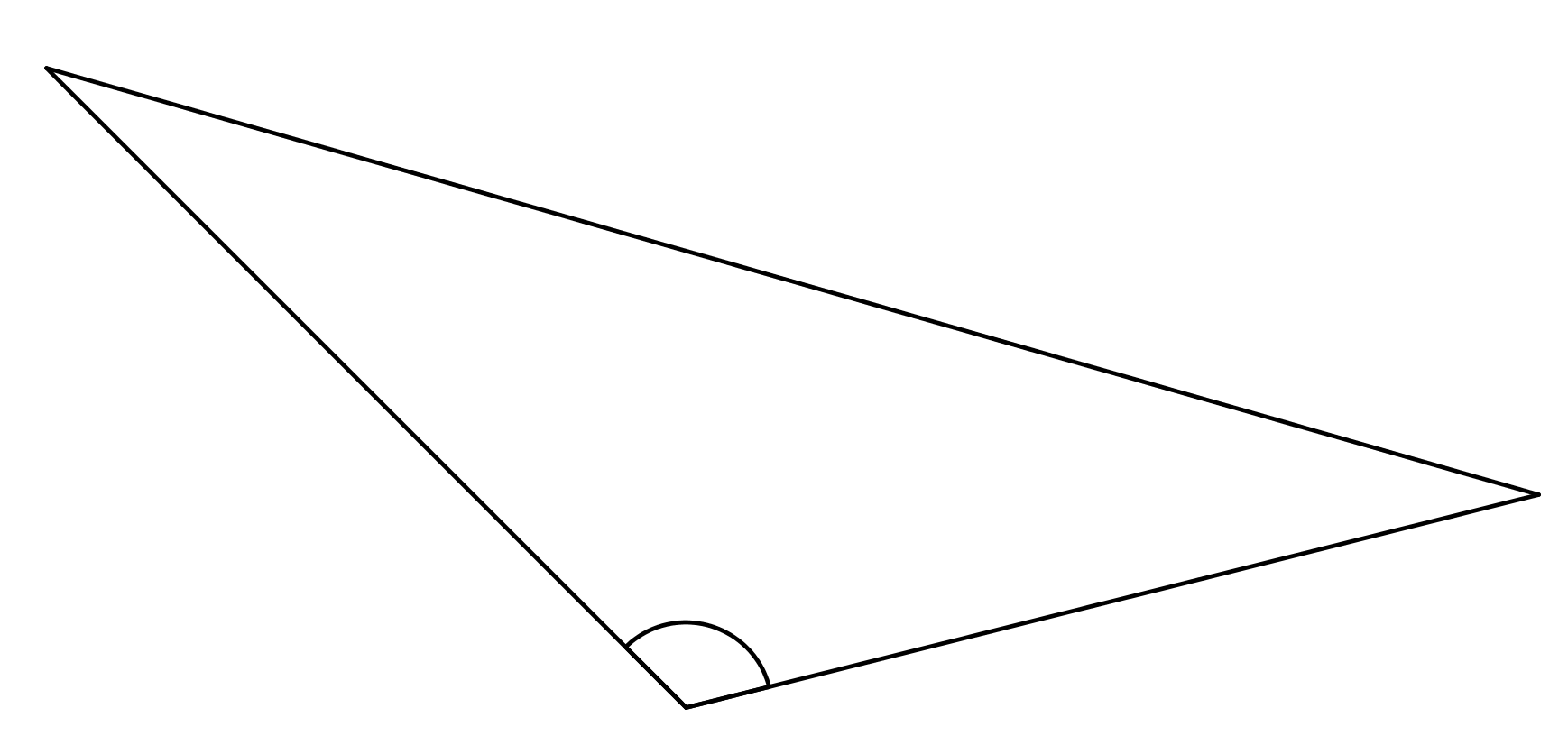
f)
Merkitse vihkoosi $\require{color}\color{red}\text{värikynällä}$ pisteesi ja puuttuvat välivaiheet.
a) suorakulmio (+1p)
b) tasakylkinen kolmio (+1p)
c) suorakulmainen kolmio (+1p)
d) suunnikas (+1p)
e) tylppäkulmainen kolmio (+1p)
f) puolisuunnikas (+1p)
Laske kulmien suuruudet.
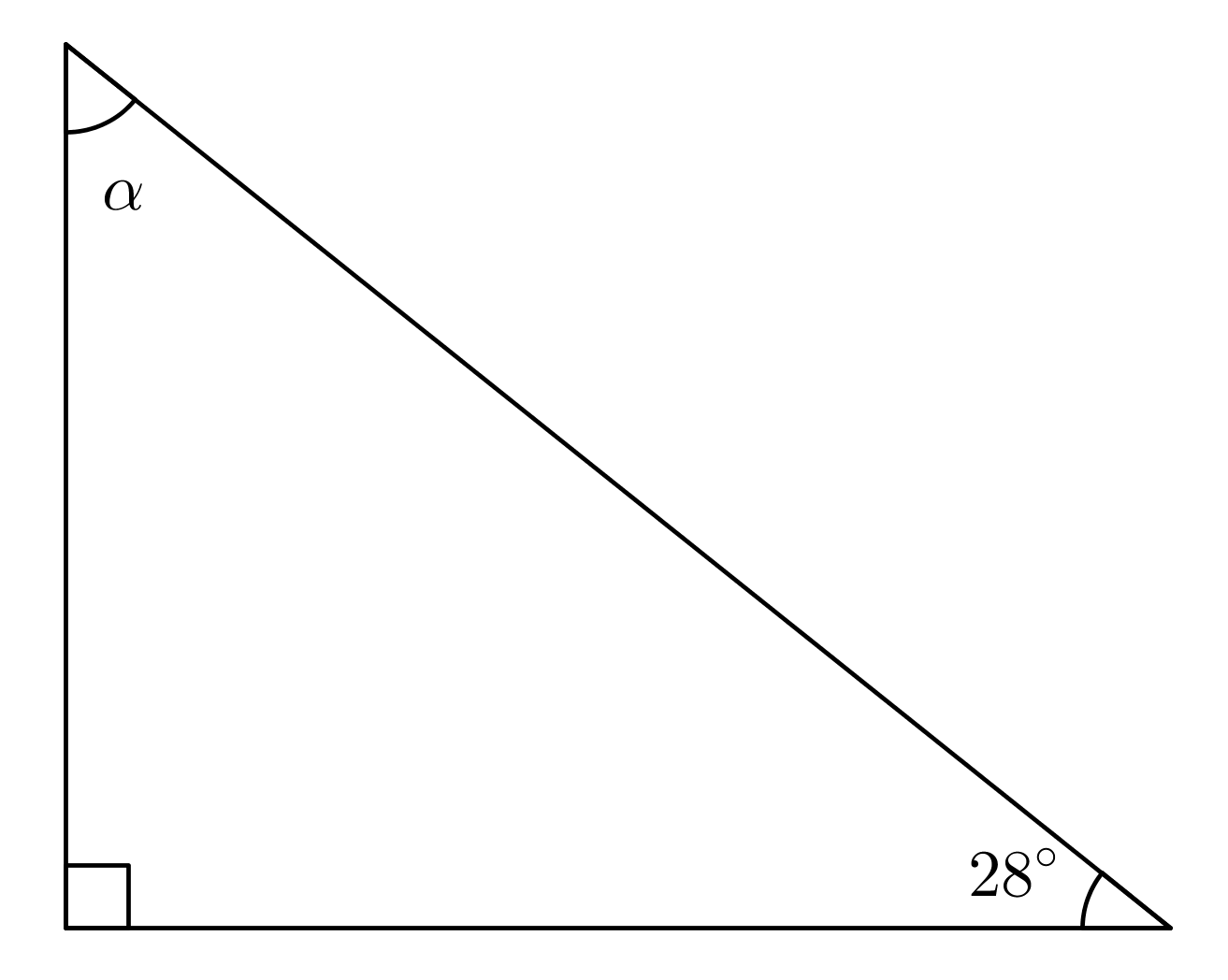
a)
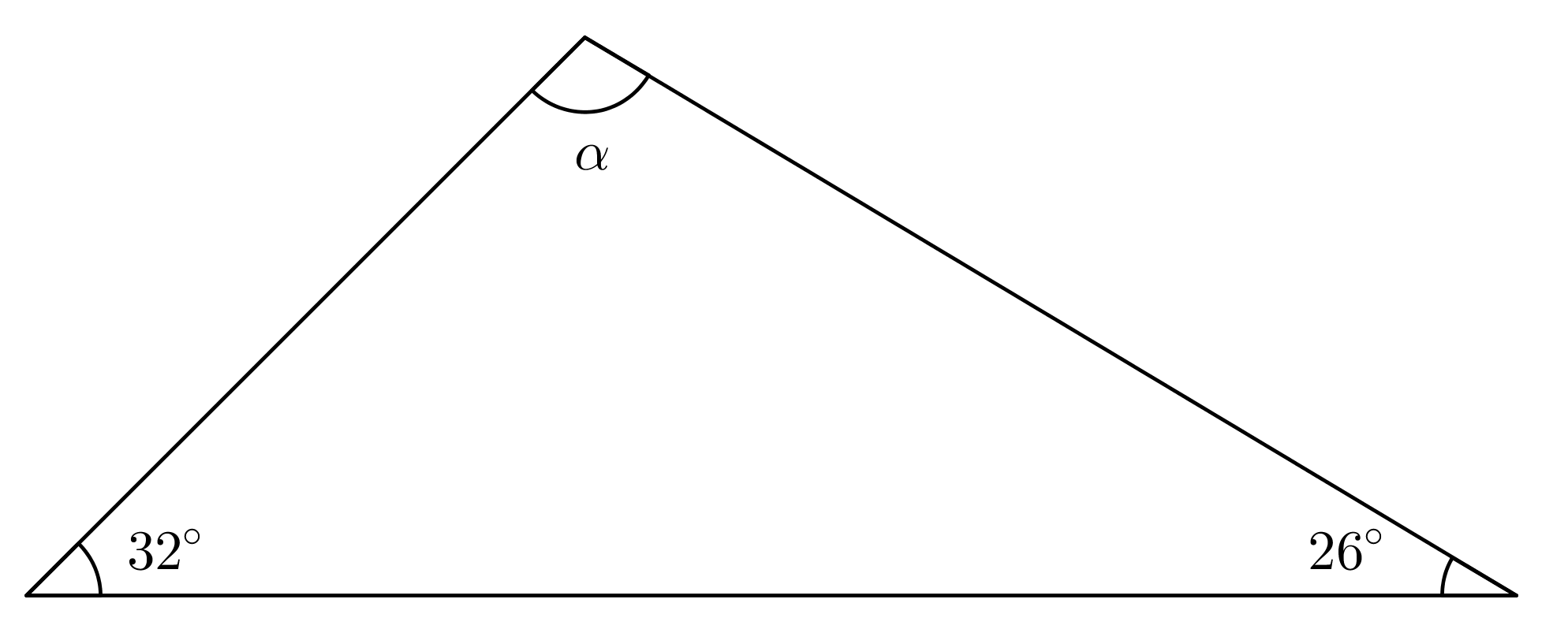
b)
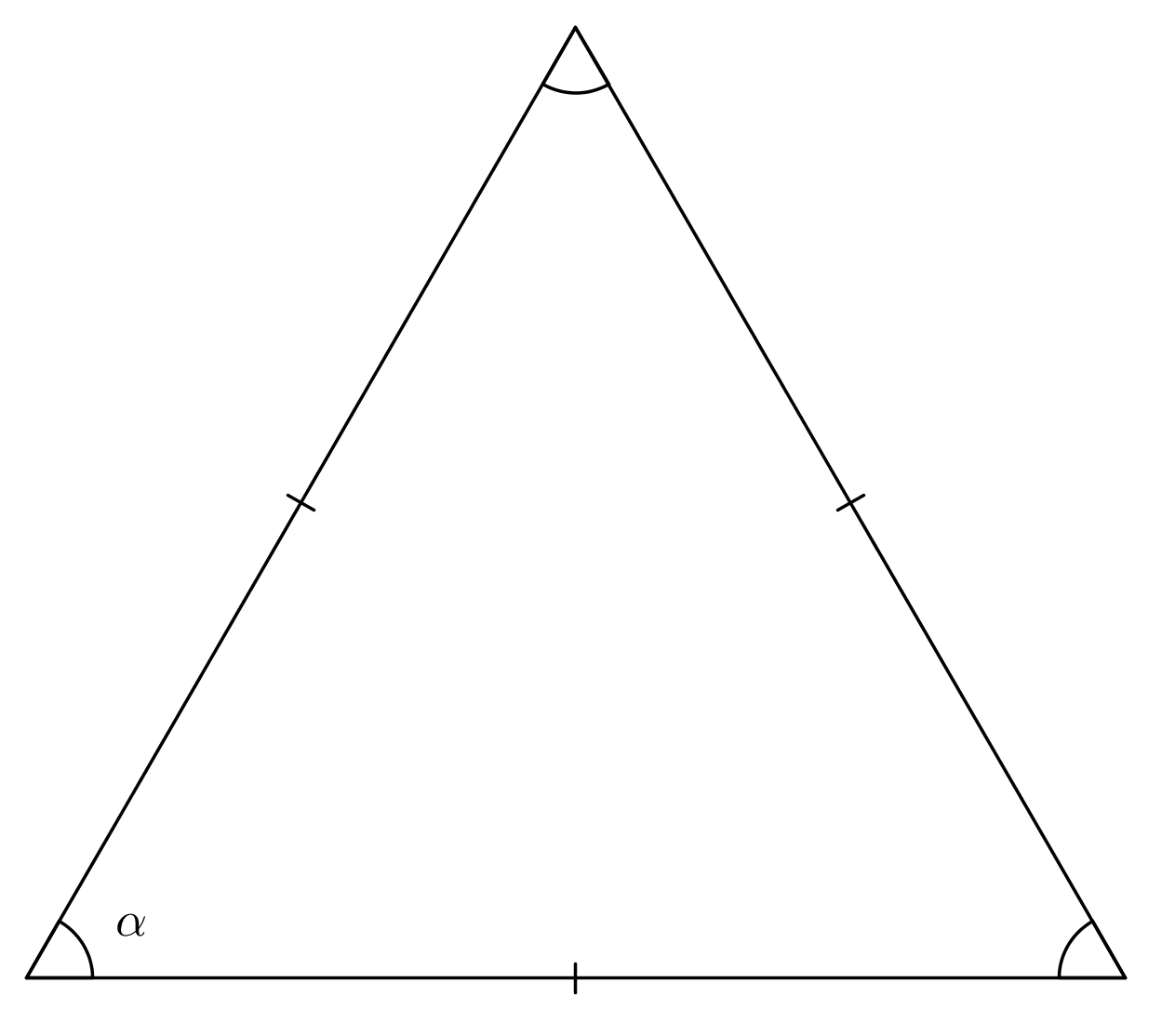
c)
Merkitse vihkoosi $\require{color}\color{red}\text{värikynällä}$ pisteesi ja puuttuvat välivaiheet.
\(\require{color} \begin{align*} \textbf{}\quad & \text{a)} \quad \alpha=180^\circ - 90^\circ - 28^\circ = 62^\circ && \color{red}{\text{(Oikea vastaus (+1p), laskulauseke (+1p))}} \\\\ & \text{b)} \quad \alpha = 180^\circ - 32^\circ - 26^\circ = 122^\circ && \color{red}{\text{(Oikea vastaus (+1p), laskulauseke (+1p))}} \\\\ & \text{c)} \quad \alpha = 180^\circ : 3 = 60^\circ && \color{red}{\text{(Oikea vastaus (+1p), laskulauseke (+1p))}} \end{align*} \)
3. a) Laske tasakylkisen kolmion huippukulman suuruus, kun kantakulma on \(34^\circ\).
b) Piirrä suunnikas, jonka sivujen pituudet ovat \(6,5cm\) ja \(4,1cm\) ja terävien kulmien suuruudet ovat \(40^\circ\).
Merkitse vihkoosi $\require{color}\color{red}\text{värikynällä}$ pisteesi ja puuttuvat välivaiheet.
\(\require{color} \begin{align*} \textbf{}\quad & \text{a)} \quad 180^\circ - 2 \cdot 34^\circ=112^\circ && \color{red}{\text{(Oikea vastaus (+1p), laskulauseke (+1p))}} \end{align*} \)
b) Pisteytysohjeet:
- kuvio on suunnikas (+1p)
- pitempi sivu on 5,6cm (+1p)
- lyhyempi sivu on 4,1cm (+1p)
- suunnikkaan pienemmät kulmat ovat 40 astetta (+1p)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
