Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Heijastuminen:
Tiedän, mitä aallon heijastuminen tarkoittaa ja osaan valon heijastumislain.
Oppimisen tueksi:
Aaltoliikkeen kohdatessa kahden aineen välisen rajapinnan tapahtuu aaltoliikkeen heijastuminen ja taittuminen.
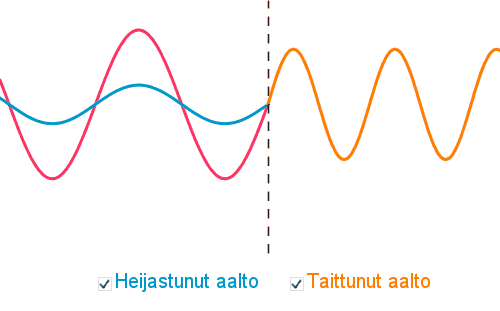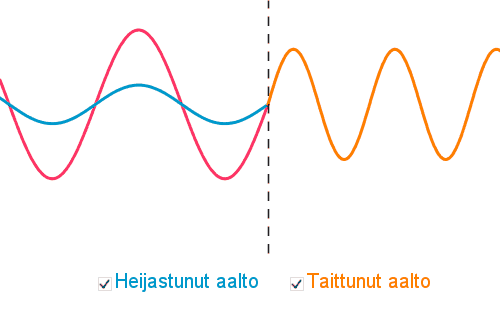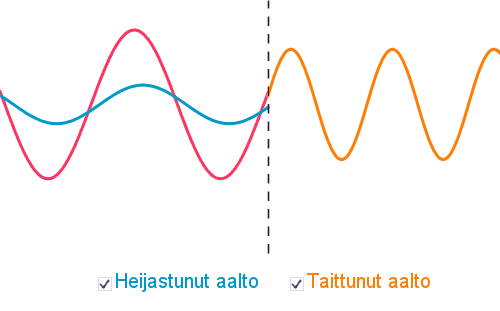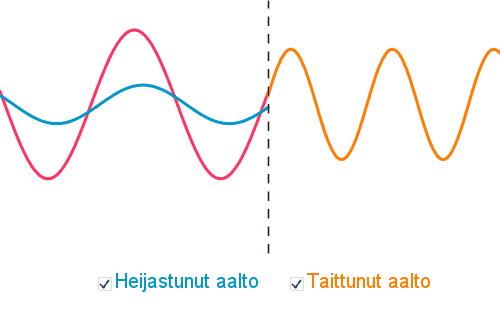
Taittumisessa on voimassa taittumislaki
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=n_{12}\)
Taittumisessa aaltoliikkeen
- aallonpituus muuttuu
- etenemisnopeus muuttuu
- taajuus pysyy samana, koska taajuuden määrää aaltolähde.
Käyttämällä aaltoliikkeen perusyhtälöä \(v=\lambda f\) taittumislaki saadaan muotoiltua aaltojen aallonpituuksille.
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=\dfrac{f \lambda_1}{f \lambda_2}=\dfrac{\lambda_1}{\lambda_2}\)
Snellin laki
- \(\color{Salmon}{\text{Punaisella tuleva valonsäde}}\)
- \(\color{Green}{\text{Vihreällä heijastunut valonsäde}}\)
- \(\color{Orange}{\text{Oranssilla taittunut valonsäde}}\)
Tulokulma ja heijastuskulma ovat yhtäsuuret eli \(\color{Salmon}{\alpha_1}=\color{Green}{\beta_1}\).
Taittumislaki valolle:
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{c_1}{c_2}=\dfrac{\lambda_1}{\lambda_2}=\color{Red}{\dfrac{n_2}{n_1}}\),
jossa \(n_1\) ja \(n_2\)ovat väliaineiden taitekertoimet.
Kokonaisheijastuminen
Kokonaisheijastumisessa aaltoliike ei taitu vaan ainoastaan heijastuu.
\(\begin{align} \dfrac{\sin \alpha_1}{\sin 90^{\circ}}&=\dfrac{n_2}{n_1} \\ \sin \alpha_1&=\dfrac{n_2}{n_1} \end{align}\)
Kokonaisheijastumisen rajakulmalle \(\alpha_r\) pätee \(\sin \alpha_r = \dfrac{n_2}{n_1}\).
Kalan näkökenttä (n.k. Snellin ikkuna)
Mitä kala tai sukeltaja näkee katsoessaan vedenpintaa?

Muistiinpanot
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Taittuminen:
Ymmärrän, mistä johtuu aaltojen taittuminen kahden aineen rajapinnassa.
Osaan myös laskea taitekulman suuruuden taittumislain avulla, jos tulokulma ja taitekertoimet tunnetaan.
Oppimisen tueksi:
Aaltoliikkeen kohdatessa kahden aineen välisen rajapinnan tapahtuu aaltoliikkeen heijastuminen ja taittuminen.

Taittumisessa on voimassa taittumislaki
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=n_{12}\)
Taittumisessa aaltoliikkeen
- aallonpituus muuttuu
- etenemisnopeus muuttuu
- taajuus pysyy samana, koska taajuuden määrää aaltolähde.
Käyttämällä aaltoliikkeen perusyhtälöä \(v=\lambda f\) taittumislaki saadaan muotoiltua aaltojen aallonpituuksille.
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=\dfrac{f \lambda_1}{f \lambda_2}=\dfrac{\lambda_1}{\lambda_2}\)
Snellin laki
- \(\color{Salmon}{\text{Punaisella tuleva valonsäde}}\)
- \(\color{Green}{\text{Vihreällä heijastunut valonsäde}}\)
- \(\color{Orange}{\text{Oranssilla taittunut valonsäde}}\)
Tulokulma ja heijastuskulma ovat yhtäsuuret eli \(\color{Salmon}{\alpha_1}=\color{Green}{\beta_1}\).
Taittumislaki valolle:
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{c_1}{c_2}=\dfrac{\lambda_1}{\lambda_2}=\color{Red}{\dfrac{n_2}{n_1}}\),
jossa \(n_1\) ja \(n_2\)ovat väliaineiden taitekertoimet.
Kokonaisheijastuminen
Kokonaisheijastumisessa aaltoliike ei taitu vaan ainoastaan heijastuu.
\(\begin{align} \dfrac{\sin \alpha_1}{\sin 90^{\circ}}&=\dfrac{n_2}{n_1} \\ \sin \alpha_1&=\dfrac{n_2}{n_1} \end{align}\)
Kokonaisheijastumisen rajakulmalle \(\alpha_r\) pätee \(\sin \alpha_r = \dfrac{n_2}{n_1}\).
Kalan näkökenttä (n.k. Snellin ikkuna)
Mitä kala tai sukeltaja näkee katsoessaan vedenpintaa?

Muistiinpanot
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Kokonaisheijastuminen:
Ymmärrän ilmiön nimeltä kokonaisheijastuminen ja osaan laskea kokonaisheijastuksen rajakulman.
Ymmärrän myös, milloin kokonaisheijastuminen on mahdollista ja milloin se ei ole mahdollista tapahtua.
Oppimisen tueksi:
Aaltoliikkeen kohdatessa kahden aineen välisen rajapinnan tapahtuu aaltoliikkeen heijastuminen ja taittuminen.

Taittumisessa on voimassa taittumislaki
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=n_{12}\)
Taittumisessa aaltoliikkeen
- aallonpituus muuttuu
- etenemisnopeus muuttuu
- taajuus pysyy samana, koska taajuuden määrää aaltolähde.
Käyttämällä aaltoliikkeen perusyhtälöä \(v=\lambda f\) taittumislaki saadaan muotoiltua aaltojen aallonpituuksille.
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=\dfrac{f \lambda_1}{f \lambda_2}=\dfrac{\lambda_1}{\lambda_2}\)
Snellin laki
- \(\color{Salmon}{\text{Punaisella tuleva valonsäde}}\)
- \(\color{Green}{\text{Vihreällä heijastunut valonsäde}}\)
- \(\color{Orange}{\text{Oranssilla taittunut valonsäde}}\)
Tulokulma ja heijastuskulma ovat yhtäsuuret eli \(\color{Salmon}{\alpha_1}=\color{Green}{\beta_1}\).
Taittumislaki valolle:
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{c_1}{c_2}=\dfrac{\lambda_1}{\lambda_2}=\color{Red}{\dfrac{n_2}{n_1}}\),
jossa \(n_1\) ja \(n_2\)ovat väliaineiden taitekertoimet.
Kokonaisheijastuminen
Kokonaisheijastumisessa aaltoliike ei taitu vaan ainoastaan heijastuu.
\(\begin{align} \dfrac{\sin \alpha_1}{\sin 90^{\circ}}&=\dfrac{n_2}{n_1} \\ \sin \alpha_1&=\dfrac{n_2}{n_1} \end{align}\)
Kokonaisheijastumisen rajakulmalle \(\alpha_r\) pätee \(\sin \alpha_r = \dfrac{n_2}{n_1}\).
Kalan näkökenttä (n.k. Snellin ikkuna)
Mitä kala tai sukeltaja näkee katsoessaan vedenpintaa?

Muistiinpanot
Täysin samaa mieltä → 6 p.
Osittain samaa mieltä → 4 p.
Osittain eri mieltä → 2 p.
Täysin eri mieltä → (jätä tyhjäksi)
(Ymmärryksen arviointiin merkitse itsellesi 6 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
