ääni ja valo
a) Värähdysliike on jaksollista liikettä \(\color{Red}{\text{(+0,5p)}}\) tasapainoaseman ympärillä \(\color{Red}{\text{(+0,5p)}}\)
b) Mekaaninen aaltoliike on liikettä, jossa häiriö etenee väliaineessa. \(\color{Red}{\text{(+1p)}}\)
(esim. ääni)
c) Sähkömagneettinen aaltoliike on aaltoliikettä, joka ei tarvitse väliainetta edetäkseen. \(\color{Red}{\text{(+1p)}}\)
(esim. valo)
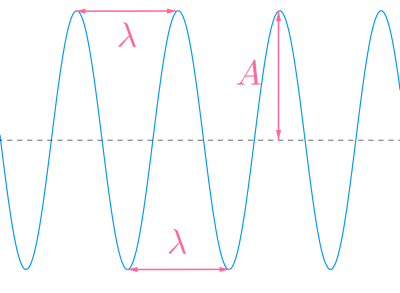
d) Amplitudi on värähdysliikkeen maksimipoikkeama \(\color{Red}{\text{(+0,5p)}}\)tasapainoasemasta \(\color{Red}{\text{(+0,5p)}}\)
e) Aallonpituus on aallon kahden peräkkäisen aallonhuipun/pohjan välinen etäisyys \(\color{Red}{\text{(+1p)}}\)
(Tai aallonpituus on aallon kahden vierekkäisen samassa vaiheessa olevan pisteen välinen etäisyys \(\color{Red}{\text{(+1p)}}\))
f) Taajuus kuvaa jonkin toistuvan ilmiön tapahtumien (esim. värähdysten) lukumäärää aikayksikköä kohti. \(\color{Red}{\text{(+1p)}}\)
(Tai taajuus on jaksonajan käänteisarvo \(\color{Red}{\text{(+1p)}}\))
Ihmisen kuuloalue on noin 20–20 000 Hz.
Millä välillä on ihmisen kuulemien äänien aallonpituus?

Äänen etenemisnopeus ilmassa on noin 343 m/s, kun ilman lämpötila on 20 celsiusastetta. \(\color{Red}{\text{(+1p)}}\)
Ääni on mekaanista aaltoliikettä, joten voimme käyttää aaltoliikkeen perusyhtälöä. \(\color{Red}{\text{(+1p)}}\)
Aaltoliikkeen perusyhtälöä käyttämällä saadaan ratkaistua äänen aallonpituus, kun tiedetään äänen etenemisnopeus ja taajuus.
\(\begin{align} v&=f \lambda \qquad&& \color{Red}{\text{(+1p)}} \\ \lambda & = \dfrac{v}{f} &&\color{Red}{\text{(+1p)}} \end{align}\)
Ratkaistaan aallonpituuden ala- ja ylärajat.
\(\lambda_{min}=\dfrac{v}{f_{max}} \\ \lambda_{min}=\dfrac{343 \text{ m/s}}{20 \ 000 \text{ Hz}} \qquad \color{Red}{\text{(+0,5p)}} \\ \lambda_{min}= 0.01715 \text{ m} \\ \lambda_{min} \approx 17 \text{ mm}\)
\(\lambda_{max}=\dfrac{v}{f_{min}} \\ \lambda_{max}=\dfrac{343 \text{ m/s}}{20 \text{ Hz}} \qquad \color{Red}{\text{(+0,5p)}}\\ \lambda_{min}= 17,15 \text{ m} \\ \lambda_{min} \approx 17 \text{ m}\)
Vastaus: Ihmisen kuulemien äänien aallonpituus on välillä 17 mm - 17 m. \(\color{Red}{\text{(+1p)}}\)
Mekaaninen aalto, jonka etenemisnopeus on 30 m/s tulee kahden aineen rajapintaan siten,
että sen tulokulma on 20 astetta ja rajapinnan taitesuhde on 1,8.
a) Laske aallon taitekulma
b) Laske taittuneen aallon nopeus.
Ratkaisu a-kohtaan:
Kirjataan lähtöarvot
\(v_1=30 \text{ m/s}, \ \alpha_1=20^{\circ}, \ n_{12}=1,8\)
Sovelletaan taittumislakia
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}=n_{12}\)
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=n_{12}\), josta
\(\sin \alpha_2=\dfrac{\sin \alpha_1}{n_{12}}\) \(\color{Red}{\text{(+1p)}}\)
Sijoitetaan tunnetut lukuarvot ja ratkaistaan taitekulma.
\(\sin \alpha_2 = \dfrac{\sin 20^{\circ}}{1,8} \) \(\color{Red}{\text{(+1p)}}\)
\(\alpha_2 =10,95 \ldots ^{\circ}\)
Vastaus: Taitekulma on noin 11 astetta. \(\color{Red}{\text{(+1p)}}\)
Ratkaisu b-kohtaan:
Sovelletaan taittumislakia
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{v_1}{v_2}\), josta
\(v_2=\dfrac{\sin \alpha_2}{\sin \alpha_1} \cdot v_1\) \(\color{Red}{\text{(+1p)}}\)
Sijoitetaan tunnetut lukuarvot.
\(v_2=\dfrac{\sin 10,95^{\circ}}{\sin 20^{\circ}} \cdot 30 \text{ m/s}\) \(\color{Red}{\text{(+1p)}}\)
\(v_2=16,661 \ldots \text{ m/s}\)
Vastaus: Taittuneen aallon nopeus on noin 17 m/s. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
