Testi on tarkoitettu kisallioppiminen.fi-sivun MAA5-kurssin itsearviointiin.
a) Määritä luvun $-2$ etäisyys nollasta itseisarvon avulla.
b) Minkä toisen luvun etäisyys nollasta on sama kuin luvun $-2$? Havainnollista päätelmäsi lukusuoralla.
c) Määritä lukujen $\frac{2}{5}$ ja $\frac{3}{4}$ välinen etäisyys.
a) Luvun etäisyyttä nollasta ilmaisee luvun itseisarvo. Koska $-2<0$, niin $|-2|=-(-2)=2$. (2 p.)
b) Hahmotellaan tilanne lukusuoralle.

Huomataan, että luvun $2$ etäisyys nollasta on sama kuin luvun $-2$ etäisyys nollasta. (Kuva 1 p., vastaus 1 p.)
c) Lukujen $\frac{2}{5}$ ja $\frac{3}{4}$ välinen etäisyys on $| \frac{2}{5}-\frac{3}{4}|$, (1 p.)
jota sieventämällä saadaan $|\frac{8}{20}-\frac{15}{20}|=|\frac{8-15}{20}|=|-\frac{7}{20}|=-\left(-\frac{7}{20}\right)=\frac{7}{20}$. (1 p.)
a) Laske pisteiden $(3,-1)$ ja $(2,5)$ välinen etäisyys. (2 p.)
b) Tavoitteena on löytää ne koordinaatiston pisteet $(x,y)$, joiden etäisyys pisteestä $(2,4)$ on viisi.
Muodosta yhtälö, joka kuvaa edellä mainittua tilannetta. (1 p.)
Piirrä koordinaatistoon tehtävänannon antamat tiedot ja päättele ainakin kaksi pistettä, jotka toteuttavat tehtävänannon. Keksitkö, mistä löytyvät kaikki yhtälön ratkaisut? Hahmottele kuvaan. (2 p.)
Osoita, että löytämäsi pisteet ovat todella ratkaisuja sijoittamalla ne aiemmin muodostamaasi yhtälöön. (1 p.)
a) Tasossa pisteiden $(x_1,y_1)$ ja $(x_2,y_2)$ välinen etäisyys on $$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2},$$ joten kysytty etäisyys on $$d=\sqrt{(2-3)^2+(5-(-1))^2}=\sqrt{(-1)^2+6^2}=\sqrt{1+36}=\sqrt{37}.$$
(Oikean kaavan käyttö (1 p.), vastaus (1 p.))
b) Pisteiden $(x,y)$ ja $(2,4)$ välinen etäisyys on $\sqrt{(x-2)^2+(y-4)^2}$ (tai $\sqrt{(2-x)^2+(4-y)^2}$).
Haluttiin, että etäisyys on viisi, joten saadaan yhtälö $\sqrt{(x-2)^2+(y-4)^2}=5$. (1 p.)
Piirretään kuva.
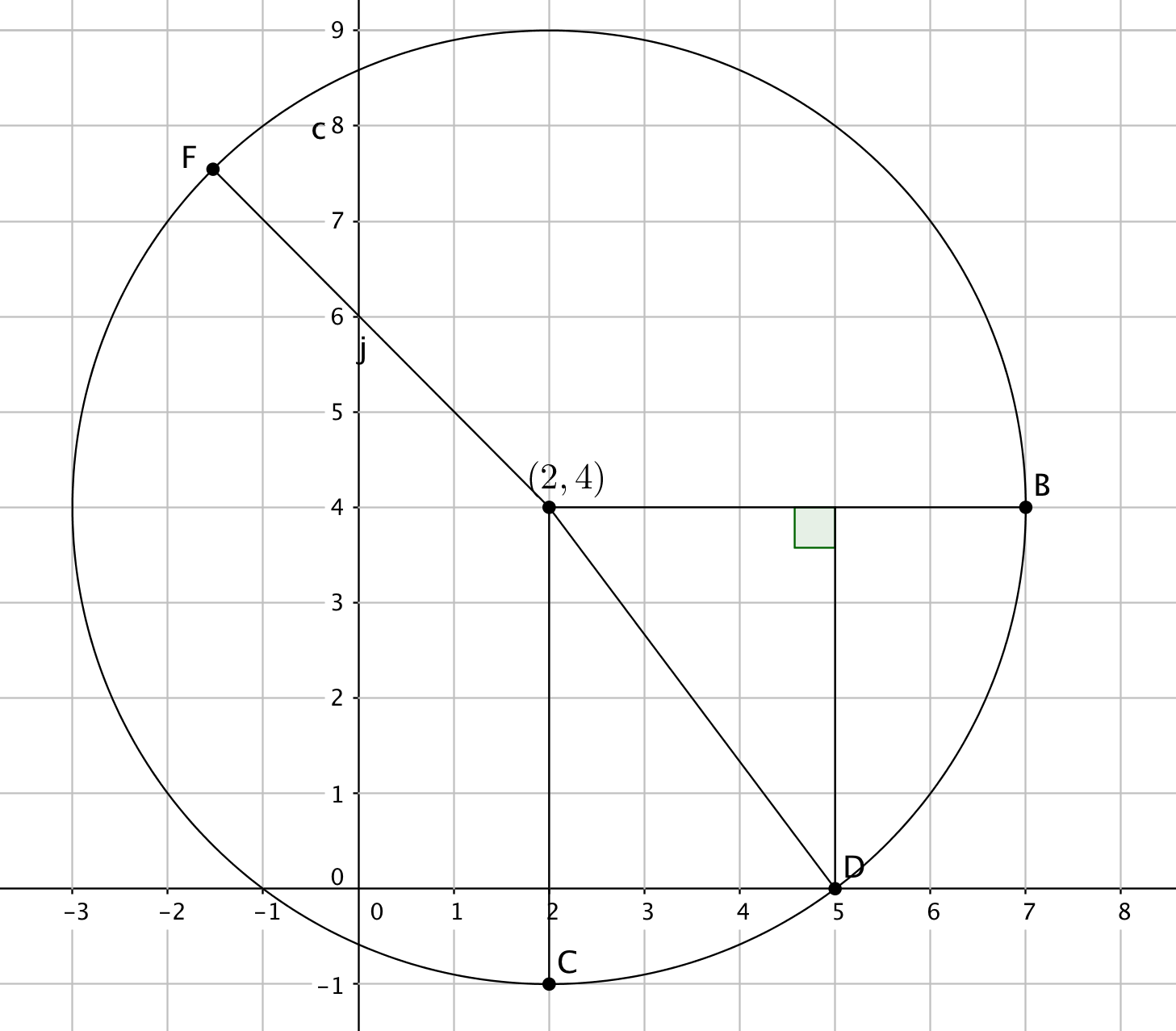
Kuvan avulla päätellään, että esimerkiksi pisteet $B=(7,4)$, $C=(2,-1)$ ja $D=(5,0)$ toteuttavat tehtävänannon. (Kuva (1 p.), kaksi oikeaa pistettä (1 p.))
Havaitaan, että kaikki sellaisen ympyrän pisteet, jonka keskipiste on $(2,4)$ ja säde $5$, ovat itse asiassa yhtälön ratkaisuja.
Sijoitetaan aluksi piste $B=(7,4)$ yhtälöön $\sqrt{(x-2)^2+(y-4)^2}=5$. Yhtälön vasemmaksi puoleksi saadaan $$\sqrt{(7-2)^2+(4-4)^2}=\sqrt{5^2+0^2}=\sqrt{25}=5,$$
joka on sama kuin yhtälön oikea puoli $5$. Siis yhtälö on tosi. Samalla tavalla osoitetaan toinen piste. (Kummatkin pisteet näytetty (1 p.))
Millä vakion $a$ arvoilla luvun $8a-10$ itseisarvo on $10-8a$?
Vihje: Palauta mieleen, mitä tiedät luvun itseisarvosta, toisin sanoen, milloin luvun itseisarvo on luku itse ja milloin luvun vastaluku. Jos tuntuu vaikealta, niin voit myös päätellä aluksi esimerkiksi jonkin vakion $a$ arvon, jolla luvun $8a-10$ itseisarvo on $10-8a$. Mieti sitten, voitko suurentaa taii pienentää keksimääsi vakiota niin, että itseisarvo pysyy edelleen muodossa $10-8a$. Etsi lopuksi kaikki mahdolliset vakion $a$ arvot.
Ensimmäinen tapa: Jos luvun $8a-10$ itseisarvo on $10-8a$, eli $|8a-10|=10-8a$, niin luvun $8a-10$ täytyy olla negatiivinen. (2 p.) Jos $8a-10$ olisi positiivinen, niin sen itseisarvo olisi luku itse, eli $|8a-10|=8a-10$.
Lisäksi luvun nolla itseisarvo voi olla $-0$ tai $0$, joten luku $8a-10$ voi olla myös nolla. (1 p.)
Siis luvun $8a-10$ täytyy toteuttaa epäyhtälö $8a-10\leq 0$. (1 p.)
Kyseessä on ensimmäisen asteen epäyhtälö, jonka voi ratkaista esimerkiksi seuraavasti:
\(\begin{align*} 8a-10&\leq10\\ 8a&\leq10\\ a&\leq\frac{10}{8}=\frac{5}{4}. \end{align*}\) (1 p.)
Vastaus: Vakion $a$ arvoilla $a\leq \frac{5}{4}$. (1 p.)
Toinen tapa (yksittäisen vakion $a$ arvon kautta päättely): Huomataan, että esimerkiksi vakion $a$ arvo $a=1$ käy, koska $8\cdot1-10=-2$, $|-2|=2$ ja toisaalta $10-8a=10-8\cdot 1=10-8=2$. (1 p.)
Lisäksi havaitaan, että jos vakiota $a$ pienentää, niin luku $8a-10$ säilyy negatiivisena, joten kaikki luvut ykkösestä alaspäin käyvät. (1 p.)
Toisaalta $|-1|=1$, joten silloin kun $8a-10=-1$, niin vastaava vakion $a$ arvo on ratkaisu, joten $a\leq 1$ ei vielä ole täydellinen ratkaisu. (1 p.)
Päätellään, että kaikki sellaiset vakion $a$ arvot, joilla $8a-10\leq 0$ (1 p.) kelpaavat ratkaisuksi, joten $a\leq \frac{5}{4}$ on lopullinen ratkaisu. (2 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
