Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA5-kurssin itsearviointiin.
Suoran kulmakerroin on $-2$ ja suora kulkee pisteen $(3,1)$ kautta.
a) Piirrä suora. (1 p.)
b) Muodosta suoran yhtälö. (2 p.)
c) Määritä jokin suoran normaalivektori. (1 p.)
c) Tutki laskemalla, onko piste $(150,-241)$ suoralla. (2 p.)
a)
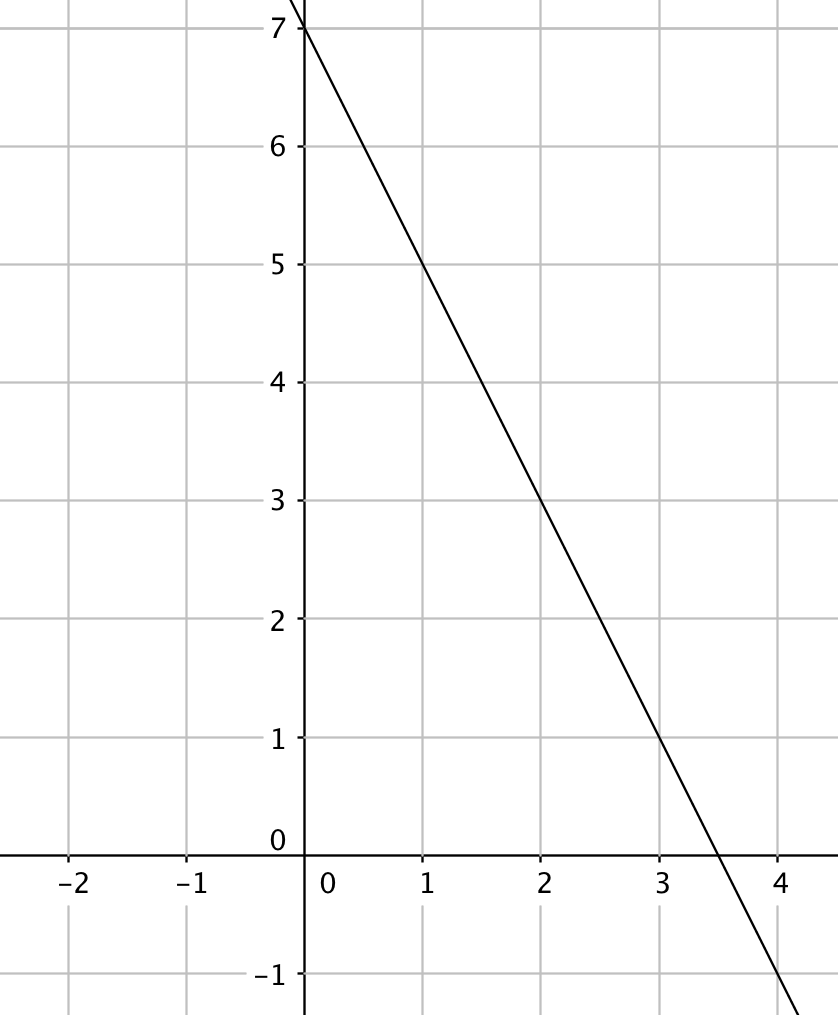(1 p.)
b) Suoran yhtälö muodostetaan kaavalla $y-y_0=k(x-x_0)$, jossa $k$ on kulmakerroin ja $(x_0,y_0)$ on jokin suoran piste. Nyt $k=-2$ ja $(x_0,y_0)=(3,1)$. Saadaan yhtälö
\(\begin{align*} y-1&=-2(x-3)\\ y-1&=-2x+6\\ y&=-2x+6+1\\ y&=-2x+7. \end{align*}\)
(Kaavaan sijoitus (1 p.), suoran yhtälö oikein (1 p.))
HUOM. Suoran yhtälön voi muodostaa muillakin tavoilla, esimerkiksi katsomalla kuvasta $y$-akselin leikkauspisteen ja päättelemällä siitä suoraan suoran yhtälön. Tämä toimii, jos leikkauspisteen koordinaatit ovat kokonaislukuja. Muilla tavoilla muodostettu suoran yhtälön pisteytys menee idealla (Perustelu (1 p.), oikea yhtälö (1 p.)).
c) Normaalivektorin voi päätellä kuvan avulla, eli kuvaan voi hahmotella vektorin, joka on kohtisuorassa suoraa vastaan. Toinen tapa määrittää normaalivektori on muokata suoran yhtälö normaalimuotoon. Saadaan $2x+y-7=0$. Normaalimuotoisesta yhtälöstä erään normaalivektorin saa suoraan kirjaimien $x$ ja $y$ kertoimista: eräs suoran normaalivektori on $2\overline{i}+\overline{j}$. (Normaalivektori oikein (1 p.) Huom. Kaikki edellä mainitun vektorin kanssa yhdensuuntaiset vektorit kelpaavat vastauksiksi.)
d) Piste $(150,-241)$ on suoralla, jos se toteuttaa suoran yhtälön. Sijoitetaan suoran yhtälöön $y=-2x+7$ $x-$koordinaatin paikalle $150$ ja tutkitaan, tuleeko vastaukseksi $-241$. Saadaan $y=-2\cdot 150+7=-300+7=-293\neq -241$ (1 p.), joten piste $(150,-241)$ ei ole suoralla. (1 p.)
a) Suoran $L_1$ yhtälö on $x-2y+4=0$ ja suora $L_2$ leikkaa $y$-akselin pisteessä $(0,4)$. Määritä suorien $L_1$ ja $L_2$ leikkauspiste, kun suorat ovat kohtisuorassa toisiaan vastaan.
b) Suora $S$ kulkee pisteiden $(-2,1)$ ja $(1,a)$ kautta. Määritä vakio $a$ siten, että suoran suuntakulma on $30^{\circ}$.
a) Muokataan ensin suoran $L_1$ yhtälöä. Saadaan $x-2y+4=0$ eli $y=\frac{1}{2}x+2$. Suoran $L_2$ kulmakerroin saadaan kohtisuoruusehdosta $k_1k_2=-1$, eli $\frac{1}{2}k=-1$, josta $k=-2$ (1 p.)
Koska suora $L_2$ leikkaa $y$-akselin pisteessä $(0,4)$, on suoran yhtälö $y=-2x+4$.
Suorien leikkauspiste saadaan selville yhtälöparista
\(\begin{cases} y&=\frac{1}{2}x+2\\ y&=-2x+4. \end{cases} \)
(Yhtälöpari (1 p.))
Merkitsemällä $y$:t yhtäsuuriksi saadaan yhtälö $\frac{1}{2}x+2=-2x+4$, josta saadaan ratkaisu $x=\frac{4}{5}$. Sijoittamalla tämä jompaankumpaan suoran yhtälöistä saadaan $y=\frac{12}{5}$, joten suorien leikkauspiste on $\left(\frac{4}{5},\frac{12}{5}\right)$. (1 p.)
Vastaus: Suorien leikkauspiste on $\left(\frac{4}{5},\frac{12}{5}\right)$.
b) Suoran suuntakulma tarkoittaa suoran ja $x$-akselin välistä kulmaa. Lisäksi, jos suora on laskeva, niin kulma on negatiivinen. Suuntakulma saadaan kaavasta $\tan \alpha =k$. Selvitetään ensin suoran $S$ kulmakerroin. Saadaan
\(\begin{align*} k=\dfrac{a-1}{1-(-2)}=\dfrac{a-1}{1+2}=\dfrac{a-1}{3}. \end{align*}\) (1 p.)
Koska suuntakulma on $30^{\circ}$, saadaan yhtälö $\tan 30^{\circ}=\dfrac{a-1}{3}$. (1 p.)
Laskimen avulla selviää, että $\tan 30^{\circ}=\frac{1}{\sqrt{3}}$, joten yhtälö saa muodon $$\dfrac{a-1}{3}=\dfrac{1}{\sqrt{3}}.$$
Ratkaistaan yhtälö
\(\begin{align*} \dfrac{a-1}{3}&=\dfrac{1}{\sqrt{3}}\\ a-1&=\dfrac{3}{\sqrt{3}}=\sqrt{3}\\ a&=\sqrt{3}+1. \end{align*}\)
(1 p.)
Vastaus: Vakion $a$ arvolla $a=\sqrt{3}+1$.
Määritä se suoran $y=3x-1$ piste, joka on lähinnä pistettä (5,2).
Tapa 1:
Hahmotellaan kuva.
(Kuva (1 p.))
Tehtävänä on selvittää kuvan pisteen $P$ koordinaatit. Muodostetaan yhtälö suoran normaalille, joka kulkee pisteen $(5,2)$ kautta. Kysytty piste on suoran ja kyseisen normaalin leikkauspiste.
Normaalin kulmakerroin saadaan kohtisuoruusehdosta $3k=-1$, josta $k=-\frac{1}{3}$. (1 p.) Normaalin yhtälöksi saadaan
\(\begin{align*} y-2&=-\frac{1}{3}(x-5)\\ y-2&=-\frac{1}{3}x+\frac{5}{3}\\ y&=-\frac{1}{3}x+\frac{11}{3}. \end{align*}\)
(Sijoitus kaavaan (1 p.), normaalin yhtälö (1 p.))
Pisteen $P$ koordinaatit saadaan yhtälöparista
\(\begin{cases} y=3x-1\\ y=-\frac{1}{3}x+\frac{11}{2}, \end{cases}\) (1 p.)
jonka ratkaisuksi saadaan esimerkiksi laskinohjelmistolla tai sijoitusmenetelmällä $x=\frac{7}{5}$ ja $y=\frac{16}{5}$.
Vastaus: Pistettä $(5,2)$ oleva suoran $y=3x-1$ lähin piste on $\left( \frac{7}{5},\frac{16}{5}\right)$. (1 p.)
Tapa 2:
Lasketaan pisteen $(5,2)$ etäisyys suorasta $y=3x-1$. Suoran yhtälö normaalimuodossa on $3x-y-1=0$. (1 p.)
Pisteen etäisyys suorasta saadaan kaavasta $d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$, jossa nyt on $(x_0,y_0)=(5,2)$ ja $ax+by+c=0$ on $3x-y-1=0$, eli $a=3, b=-1$ ja $c=-1$. (1 p.)
Etäisyys on
\(\begin{align*} d&=\dfrac{|3\cdot 5-1\cdot 2-1|}{\sqrt{3^2+(-1)^2}}=\dfrac{12}{\sqrt{10}}. \end{align*}\) (1 p.)
Merkitään kysyttyä suoran pistettä $(x,y)$. Koska piste on suoralla $y=3x-1$, voidaan piste lausua muodossa $(x,3x+1)$. (1 p.) Nyt tämän sekä pisteen $(5,2)$ etäisyys pitää olla $\dfrac{12}{\sqrt{10}}$, joten saadaan yhtälö $$\sqrt{(x-5)^2+((3x-1)-2)^2}=\dfrac{12}{\sqrt{10}},$$
joka sievenee muotoon $$\sqrt{10x^2-28x+34}=\dfrac{12}{\sqrt{10}}.$$
(1 p.)
Yhtälö on kohtuullisen työläs ja sen voi hyvin ratkaista tässä kohtaa laskinohjelmistolla. Ratkaisuksi saadaan $x=\frac{7}{5}$, jolloin $y=3\cdot \frac{7}{5}-1=\frac{16}{5}$.
Vastaus:
Pistettä $(5,2)$ oleva suoran $y=3x-1$ lähin piste on $\left( \frac{7}{5},\frac{16}{5}\right)$. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: