Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA6-kurssin itsearviointiin.
a) Määritä $f'(2)$ derivaatan määritelmän avulla, kun $f(x)=2x-1$.
b) Tehtävänä oli tutkia funktion $f(x)$ derivoituvuutta kohdassa $x=1$, kun \(f(x)=\begin{cases} -x+2, x\leq1\\ \dfrac{x^2-1}{1-x}, x>1 \end{cases}\). Opiskelija A laski erotusosamäärän vasemman- ja oikeanpuoleisen raja-arvon kohdassa $x=1$ ja sai
\(\begin{align*} \lim_{x\rightarrow 1-}\dfrac{f(x)-f(1)}{x-1}&=\lim_{x\rightarrow 1-} \dfrac{-x+2-(-1+2)}{x-1}=\lim_{x\rightarrow 1-}\dfrac{-x+1}{x-1}=\lim_{x\rightarrow 1-}(-1)=-1 \text{ ja}\\ \lim_{x\rightarrow 1+} \dfrac{f(x)-f(1)}{x-1}&=\lim_{x\rightarrow 1+} \dfrac{\frac{x^2-1}{1-x}-(-1+2)}{x-1}=\lim_{x\rightarrow 1+}\dfrac{\frac{(x+1)(x-1)}{-(x-1)}-1}{x-1}=\lim_{x\rightarrow 1+}\dfrac{-x-1-1}{x-1}=\lim_{x\rightarrow 1+}\dfrac{-x-2}{x-1}. \end{align*}\)
Koska lauseke $\dfrac{-x-2}{x-1}$ ei supistu, niin oikeanpuoleista erotusosamäärän raja-arvoa ei ole olemassa ja näin ollen $f(x)$ ei ole derivoituva kohdassa $x=1$.
Opiskelija B tarkasteli funktion $f(x)$ jatkuvuutta ja sai
\(\begin{align*} \lim_{x\rightarrow 1-} f(x)&=\lim_{x\rightarrow 1-} (-x+2)=-1+2=1 \text{ ja}\\ \lim_{x\rightarrow 1+}f(x)&=\lim_{x\rightarrow 1+} \dfrac{x^2-1}{1-x}=\lim_{x\rightarrow 1+}\dfrac{(x+1)(x-1)}{-(x-1)}=\lim_{x\rightarrow 1+}\dfrac{x+1}{-1}=\lim_{x\rightarrow 1+}(-x-1)=-1-1=-2. \end{align*}\)
Koska vasemman- ja oikeanpuoleiset raja-arvot ovat eri suuret, niin funktiolla ei ole raja-arvoa kohdassa $x=1$ eli funktio ei voi olla jatkuva kohdassa $x=1$. Näin ollen funktio ei ole derivoituva kohdassa $x=1$.
Oliko opiskelijoiden johtopäätökset oikeita? Olivatko heidän perustelunsa oikein?
a) Määritetään erotusosamäärän raja-arvo kohdassa $x=2$.
\(\begin{align*} \lim_{x\rightarrow 2}\dfrac{f(x)-f(2)}{x-2}=\lim_{x\rightarrow 2}\dfrac{(2x-1)-(2\cdot 2-1)}{x-2}=\lim_{x\rightarrow 2}=\dfrac{2x-1-3}{x-2}=\lim_{x\rightarrow 2}\dfrac{2(x-2)}{x-2}=\lim_{x\rightarrow 2}(2)=2. \end{align*}\)
(Erotusosamäärä oikein muodostettu (1 p.), lauseke supistettu (1 p.), vastaus (1 p.))
Siis $f'(2)=2$.
b) Kummankin opiskelijan johtopäätökset olivat oikeat. (1 p.)
Opiskelija A oli oikeassa, koska derivoituvuutta tutkitaan erotusosamäärän raja-arvon avulla ja raja-arvoa ei ollut ko. tehtävässä olemassa. (1 p.)
Opiskelija B oli oikeassa, koska vain jatkuva funktio voi olla derivoituva. (Teoreema 3 (Jos funktio on derivoituva kohdassa $a$, niin funktio on jatkuva kohdassa $a$) on yhtäpitävä teoreeman "Jos funktio ei ole jatkuva kohdassa $a$, niin funktio ei ole derivoituva kohdassa $a$" kanssa.) (1 p.)
Derivoi ja määritä derivaattafunktion arvo kohdassa $x=-1$.
a) $f(x)=x^5$
b) $g(x)=x^3+x$
c) $h(x)=2x^4-\frac{1}{3}x^3+2$.
a) $f(x)=5x^4$ (1 p.), joten $f'(-1)=5\cdot (-1)^4=5$. (1 p.)
b) $g(x)=3x^2+1$ (1 p.), joten $g'(-1)=3\cdot (-1)^2+1=4$. (1 p.)
c) $h'(x)=2\cdot 4x^3-\frac{1}{3}\cdot 3x^2+0=8x^3-x^2$ (1 p.), joten $h'(-1)=8\cdot (-1)^3-(-1)^2=-8-1=-9$. (1 p.)
Tarkastellaan käyrää $y=-x^3+5x-1$.
a) Käyrälle piirretään tangentti kohtaan $x=1$. Määritä tangentin yhtälö.
b) Määritä kohdat, johon piirretyt tangentit ovat yhdensuuntaisia a)-kohdan tangentin kanssa.
a) Tangentin kulmakerroin on derivaatan arvo kohdassa $x=1$.
$y'=-3x^2+5$, josta $y'(1)=-3\cdot1^2+5=2$. (1 p.)
Selvitetään vielä, mikä on $y$-koordinaatti, kun $x=1$. $y=-1^3+5\cdot1-1=3$. (1 p.)
Tangentin yhtälöksi saadaan
\(\begin{align*} y-3&=2(x-1)\\ y-3&=2x-2\\ y&=2x-2+3=2x+1 \end{align*}\) (1 p.)
b) Selvitetään, millä muuttujan $x$ arvoilla y'(x)=2. (1 p.)
Saadaan yhtälö $-3x^2+5=2$, josta $-3x^2=-3$ ja $x^2=1$. Yhtälö on tosi, kun $x=1$ tai $x=-1$. (1 p.)
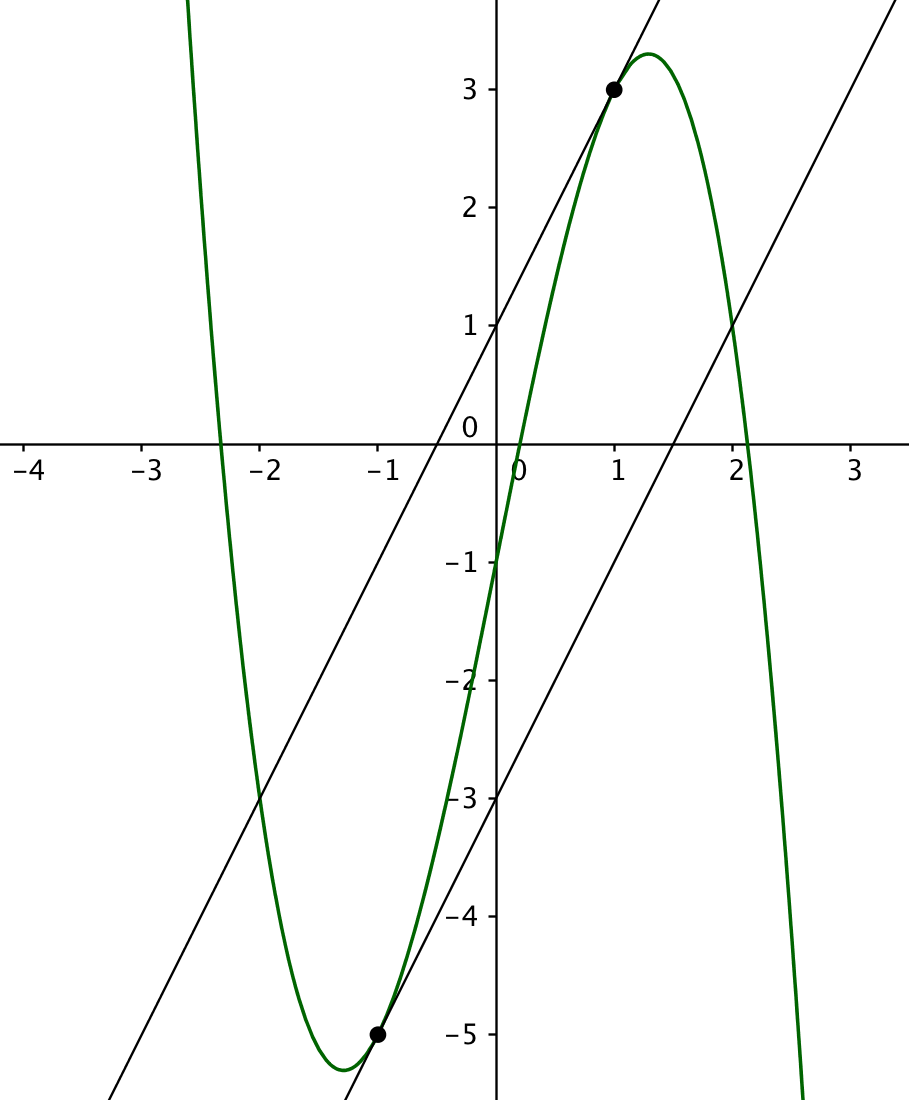
Siis kohtaan $x=-1$ piirretty tangentti on yhdensuuntainen kohtaan $x=1$ piirretyn tangentin kanssa. (1 p.)
Alla vielä kuva tilanteesta.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
