Testi on tarkoitettu kisallioppiminen.fi -sivuston MAA7-kurssin itsearviointiin.
a) Alla olevaan kuvaan on piirretty eräs kulma $\alpha$. Määritä yhden desimaalin tarkkuudella $\sin\alpha, \cos\alpha$ ja $\tan \alpha$.
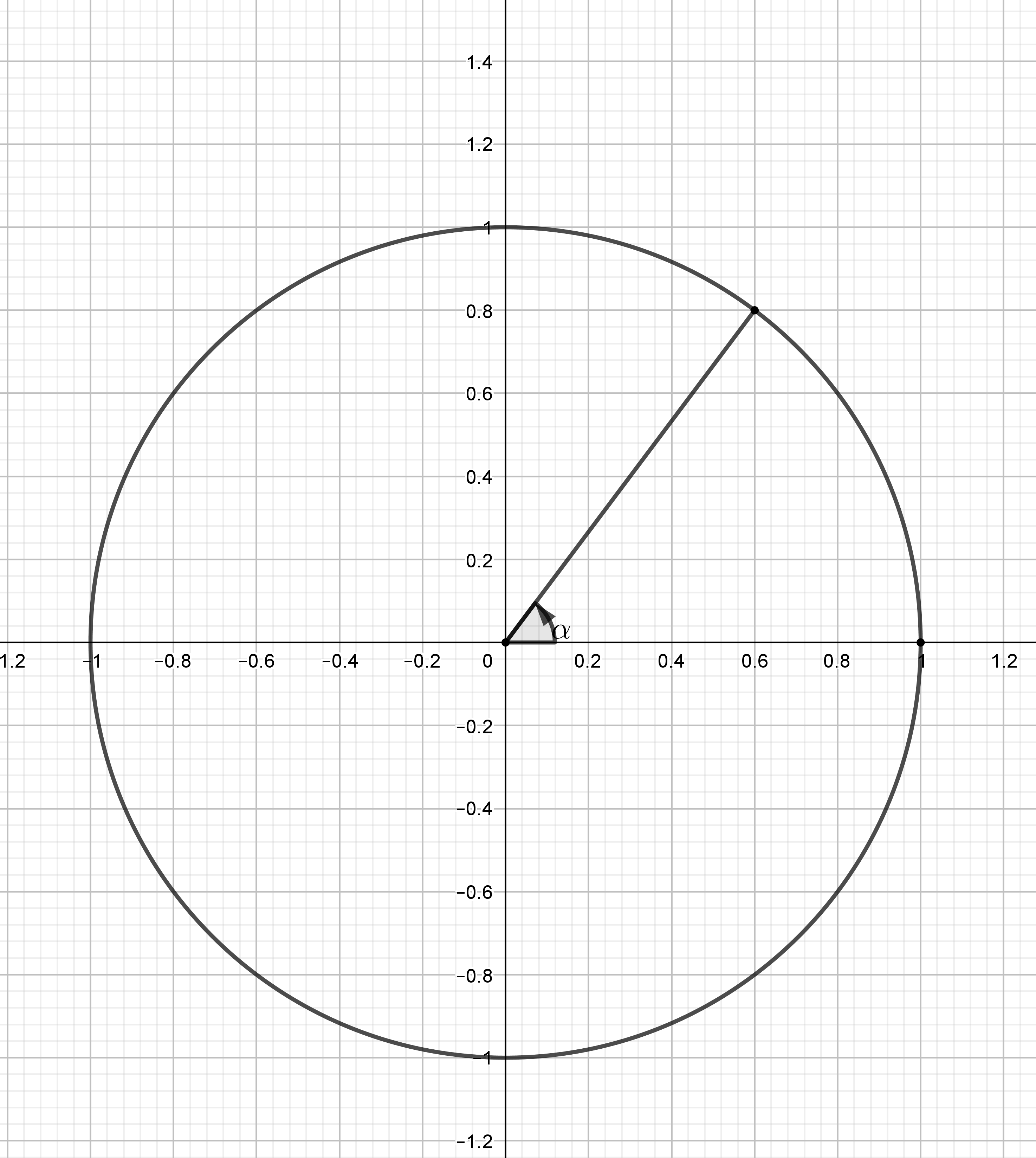
b) Piirrä yksikköympyrään kolme eri kulmaa, joille pätee $\sin \alpha=0{,}4$. Kaikilla kulmilla ei saa olla sama loppukylki.
a) $\sin \alpha\approx 0{,}8$ (1 p.), $\cos \alpha \approx 0{,}6$ (1 p.) ja $\tan \alpha\approx 1{,}3$ (1 p.). Tangentin määrittämistä varten pitää piirtää ympyrälle tangentti pisteeseen $(1,0)$ sekä kulman loppukyljen jatke siten, että jatke ja tangentti leikkaavat. Toinen vaihtoehto on käyttää tietoa $\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}$.
b) Kulmat voivat olla esimerkiksi seuraavanlaisia.
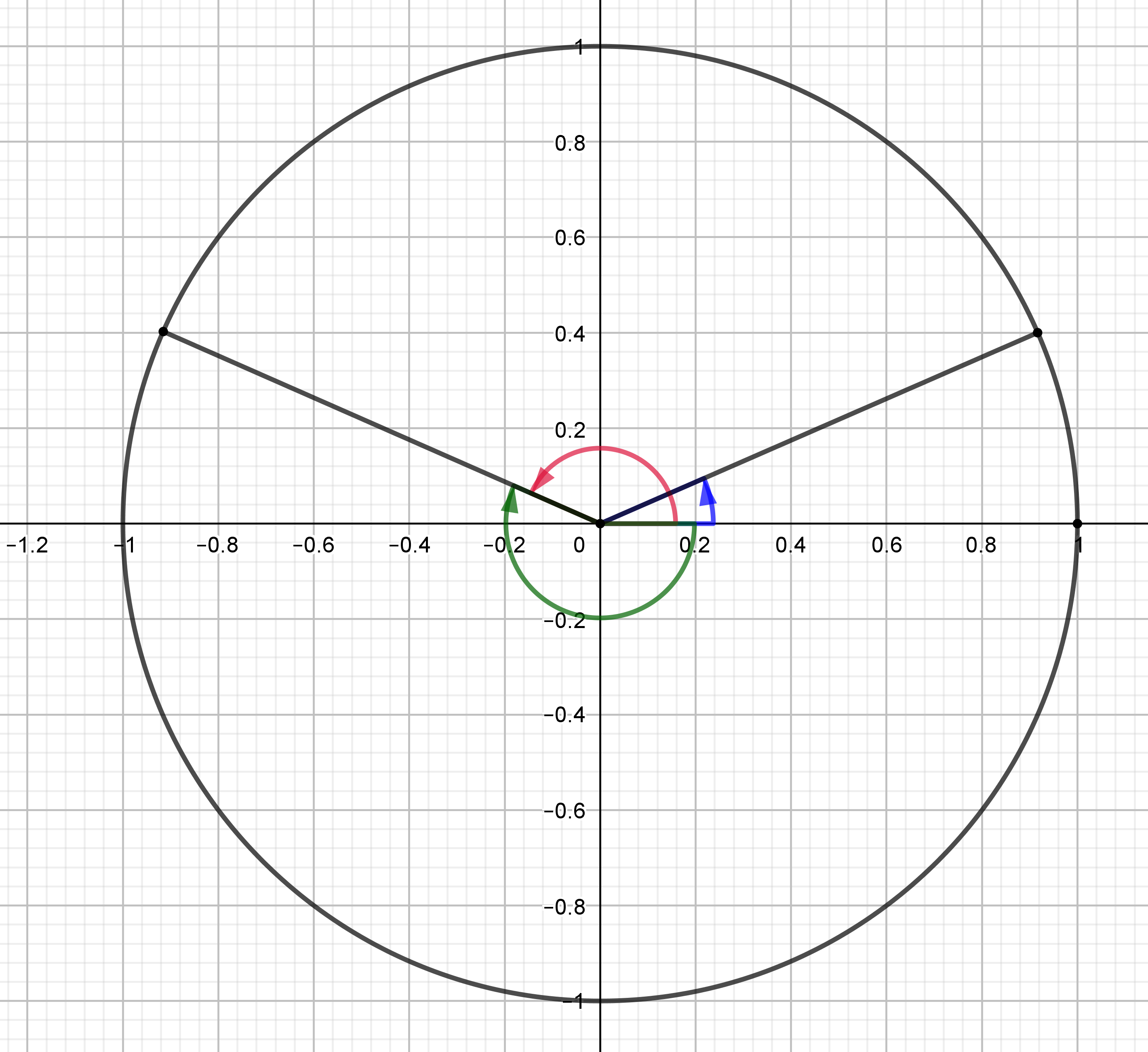
((1 p.) oikeasta kulmasta, eli yhteensä max. (3 p.))
a) Ratkaise yhtälö $\sin \alpha=\dfrac{\sqrt{3}}{2}$.
b) Ratkaise yhtälö $\cos (2\alpha)=\cos (40^{\circ})$.
a) Etsitään ensin laskimen tai taulukkokirjan avulla yksi ratkaisu yhtälölle $\sin \alpha=\dfrac{\sqrt{3}}{2}$. Saadaan $\sin \alpha=\dfrac{\sqrt{3}}{2}$, kun $\alpha=60^{\circ}$. (1 p.)
Yksikköympyrään hahmottelun tai sinin ominaisuuksien perusteella päätellään, että tällöin myös $\alpha=180^\circ-60^{\circ}=120^{\circ}$ on eräs ratkaisu. (1 p.)
Koska etsitään yhtälölle kaikkia mahdollisia ratkaisuja, niin myös kyseisten kulmien jaksojen monikerrat kelpaavat ratkaisuiksi, eli esimerkiksi $\alpha=60^{\circ}+360^{\circ}=420^{\circ}$. Näin ollen yhtälön ratkaisuksi saadaan
\(\begin{align*} &\alpha=60^{\circ}+n\cdot 360^{\circ} \text{ tai } \alpha=120^{\circ}+n\cdot 360^{\circ},\\ &\text{missä } n \text{ on kokonaisluku.} \end{align*}\)(1 p.)
Huom. Ratkaisu voi edetä myös suoraan seuraavasti:
\(\begin{align*} \sin \alpha&=\dfrac{\sqrt{3}}{2}\\ \alpha&=60^{\circ}+n\cdot360^{\circ} \text{ tai } \alpha=120^{\circ}+n\cdot 360^{\circ}, \text{ missä } n \text{ on kokonaisluku.} \end{align*}\)
Tällöin pisteet tulevat samalla idealla, eli yhdestä ratkaisusta piste, suplementtikulmasta toinen piste ja lopullisesta ratkaisuista jakson monikertoineen kolmas piste.
b) Hahmotellaan yhtälön tilanteesta kuva.
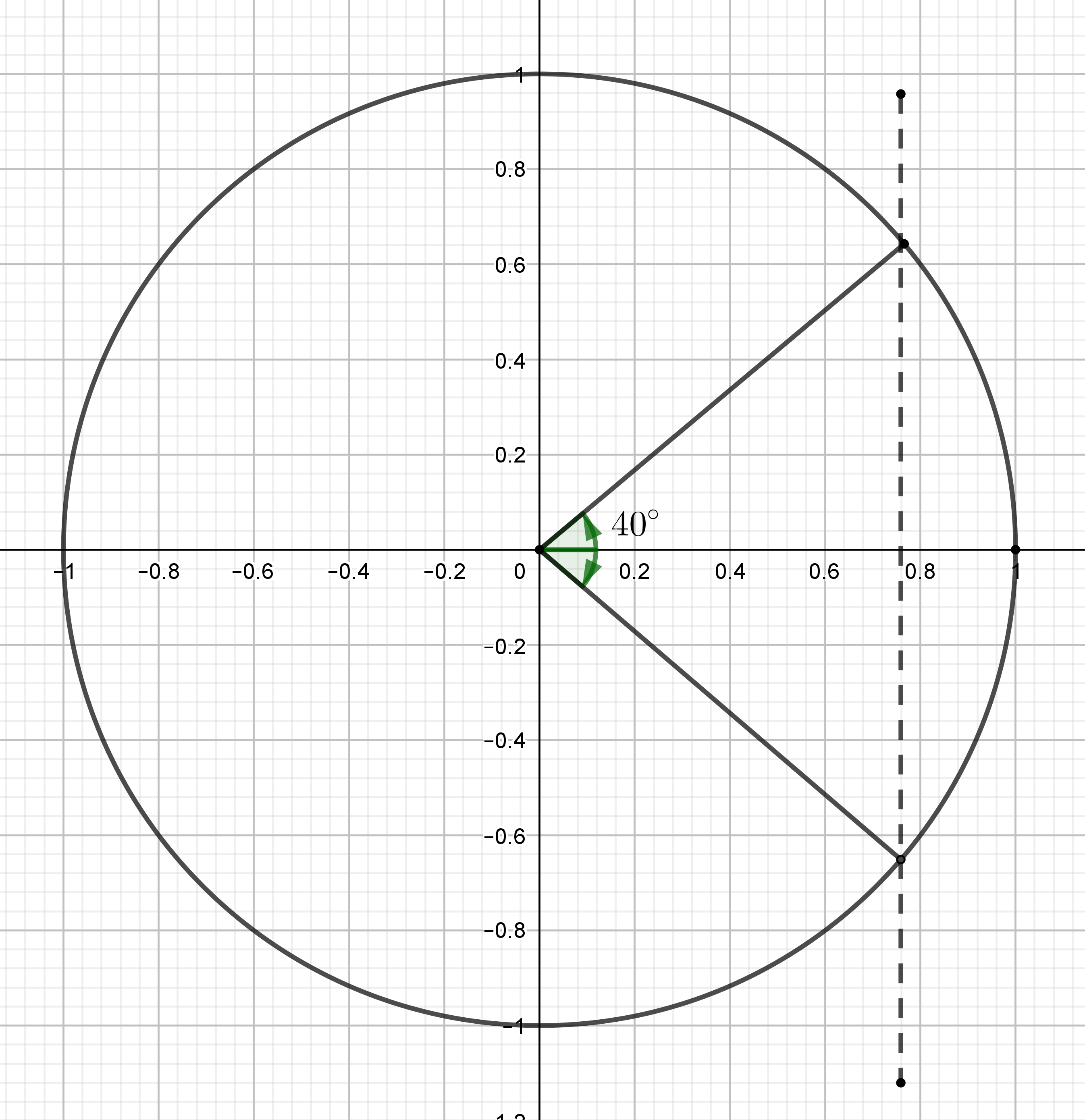
Kuvasta huomataan, että yhtälössä $\cos (2\alpha)=\cos (40^{\circ})$ on annettu kulmalle $2\alpha$ jo yksi ratkaisu: $2\alpha=40^{\circ}$. (1 p.)
Toisin sanoen, kosinin arvoa $\cos 40^{\circ}$ ei tarvitse edes tietää. Jos kuitenkin sen on laskimesta katsonut ja jatkanut sen jälkeen tehtävää oikein, niin ei siinä varsinaista virhettä ole tapahtunut.
Kosinin kohdalla toinen kulma, joka toteuttaa ehdon $\cos (2 \alpha)=\cos 40^{\circ}$ on kulman $40^{\circ}$ vastakulma, eli $2\alpha=-40^{\circ}$. (1 p.)
Koska kosinin jakson pituus on $360^{\circ}$, niin kaikki ratkaisut ovat muotoa $2\alpha=\pm40^{\circ}+n\cdot 360^{\circ}$, missä $n$ on kokonaisluku. Tämä ei kuitenkaan ole vielä lopullinen ratkaisu, koska olemme vasta selvittäneet kulman $2\alpha$ suuruuden. Jakamalla yhtälöä $2\alpha=\pm40^{\circ}+n\cdot 360^{\circ}$ luvulla $2$ saamme lopulliset ratkaisut, eli
\(\begin{align*} &\alpha=\pm20^{\circ}+n\cdot 180^{\circ},\\ &\text{missä }n \text{ on kokonaisluku.} \end{align*}\)(1 p.)
Huom. Taas ratkaisun voi kirjoittaa myös suoraan allekkain seuraavasti:
\(\begin{align*} \cos (2\alpha)&=\cos (40^{\circ})\\ 2\alpha&=\pm40^{\circ}+n\cdot 360^{\circ}\\ \alpha&=\pm20^{\circ}+n\cdot 180^{\circ}, \text{ missä } n \text{ on kokonaisluku.} \end{align*}\)
a) Ratkaise yhtälö $2\tan \alpha -3=0$. Anna vastaus asteen tarkkuudella.
b) Ratkaise yhtälö $3\sin\alpha=5\cos\alpha$. Anna vastaus asteen tarkkuudella.
a) Muokataan ensin yhtälö muotoon $\tan \alpha=a$, missä $a$ on joku luku. Saadaan
\(\begin{align*} 2\tan \alpha -3&=0\\ 2\tan \alpha &=3\\ \tan \alpha &=\dfrac{3}{2}. \end{align*}\)(1 p.)
Selvitetään yksi ratkaisu laskimesta $\tan^{-1}$ avulla. Selviää, että $\alpha=56{,}3\ldots^{\circ}\approx56^{\circ}$ on eräs ratkaisu. (1 p.) Koska tangentin jakson pituus on $180^{\circ}$, niin kaikki ratkaisut ovat muotoa
\(\begin{align*} &\alpha\approx 56^{\circ}+n\cdot 180^{\circ},\\ &\text{missä } n \text{ on kokonaisluku.} \end{align*}\)(1 p.)
b) Koska yhtälössä $3\sin\alpha=5\cos\alpha$ esiintyy sekä siniä että kosinia ja niillä on eri kertoimet, pitää yhtälö muokata tangenttiyhtälöksi. Käytetään siis tietoa $\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}$. Saadaan
\(\begin{align*} 3\sin\alpha&=5\cos\alpha \quad || :3\\ \sin \alpha&=\dfrac{5\cos \alpha}{3} \quad || :\cos \alpha\neq 0\\ \dfrac{\sin \alpha}{\cos \alpha}&=\dfrac{5}{3}\\ \tan \alpha&=\dfrac{5}{3}. \end{align*}\)(1 p.)
Tämä yhtälö toteutuu, kun $\alpha=59{,}3\ldots^{\circ}+n\cdot 180^{\circ}\approx59^{\circ}+n\cdot 180^{\circ}$, missä $n$ on kokonaisluku. (1 p.)
Koska jaettaessa yhtälöä lausekkeella $\cos \alpha$ jouduimme olettamaan, että $\cos \alpha\neq 0$, niin tutkimme erikseen, mitä tapahtuu, jos $\cos \alpha=0$. Tällöin yhtälö $3\sin\alpha=5\cos\alpha$ saa muodon $3\sin \alpha=0$, eli $\sin \alpha=0$. Koska sinillä ja kosinilla ei ole yhteisiä nollakohtia, niin yhtälölle ei löydy ratkaisua, eli yhtälöllä $3\sin\alpha=5\cos\alpha$ on ratkaisuja vain, jos $\cos \alpha\neq 0$. (Kosinin nollakohtien tarkastelu 1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
