Testi on tarkoitettu kisallioppiminen.fi -sivuston MAB3-kurssin itsearviointiin.
a) Tasasivuisen kolmion sivun pituus on 4. Laske kolmion pinta-ala.
b) Laske alla olevan puolisuunnikkaan pinta-ala.

a) Piirretään mallikuva.
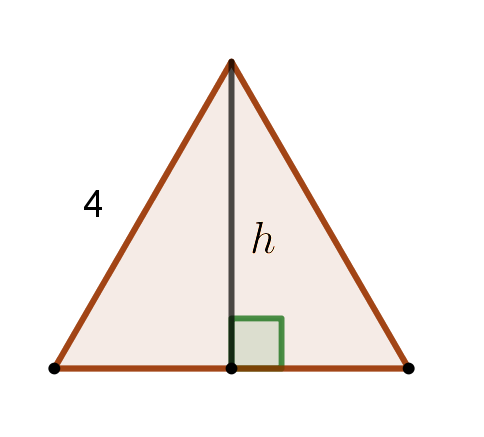
Korkeusjana puolittaa kannan, joten korkeus saadaan Pythagoraan lauseella.
$2^2+h^2=4^2$ (1 p.)
$h^2=16-4$
$h^2=12$
$h=\pm\sqrt{12}$ Koska $h>0$, niin
$h=\sqrt{12}$. (1 p.)
Pinta-ala on $A=\dfrac{4\cdot\sqrt{12}}{2}=2\sqrt{12}$. (1 p.)
HUOM. Koska tehtävänannossa ei esiintynyt yksiköitä, annetaan vastaus tarkkana arvona. Lisäksi voi halutessaan antaa likiarvon.
HUOM. Korkeusjanan pituuden voisi myös ratkaista suorakulmaisen kolmion trigonometrialla, koska tasasivuisessa kolmiossa kaikki kulmat ovat 60 astetta.
b) Täydennetään kuvaa.

Ratkaistaan korkeus suorakulmaisesta kolmiosta.
$sin(60^{\circ}=\frac{h}{6,9}$ (1 p.)
$h=6,9\sin(60^{\circ})=5,975\ldots$ (cm) (1 p.)
Pinta-ala on tällöin $A=\dfrac{(5+2,5)\cdot 5,975\ldots}{2}=22,40\ldots\approx 22$ (cm$^2)$.
Vastaus: Pinta-ala on 22 cm$^2$. (1 p.)
Julisteen pinta-ala on 12 dm$^2$ ja lyhyemmän sivun pituus on 30 cm. Mikä on toisen julisteen lyhyemmän sivun pituus, kun sen pinta-ala on 432 cm$^2$ ja julisteet ovat yhdenmuotoiset?
Muutetaan pinta-alat ensin samaan yksikköön.
$12$ dm$^2=1200$ cm$^2$. (1 p.)
Yhdenmuotoisilla kuvioille pätee, että pinta-alojen suhde on yhdenmuotoisuussuhteen neliö, eli
$\dfrac{A_1}{A_2}=\left( \dfrac{m}{n} \right)^2$. (1 p.)
Tehtävänannon tiedoilla saadaan yhtälö
$\dfrac{1200}{432}=\left( \dfrac{30}{x} \right)^2$ (Vasen puoli yhtälöstä (1 p.), oikea puoli yhtälöstä (1 p.))
Laskinohjelmistolla ratkaisun voi ottaa suoraan. Jos sieventää käsin, niin välivaiheet olisivat seuraavat:
$\dfrac{1200}{432}=\dfrac{30^2}{x^2}$
$1200x^2=432\cdot900$
$x^2=\dfrac{432\cdot 900}{1200}=324$
$x=\pm \sqrt{324}$ Koska $x>0$,
$x=18$. (1 p.)
Vastaus: Julisteen lyhyemmän sivun pituus on 18 cm. (1 p.)
a) Laske kuvassa näkyvän kaaren pituus $b$ yhden desimaalin tarkkuudella.

b) Kuinka kauas on mahdollista nähdä Stadionin tornista, joka on 72 m merenpinnan yläpuolella? Maapallon säde on noin 6370 km ja etäisyys mitataan maapallon pintaa pitkin.
a) Kuvaan piirretyt janat ovat ympyrän tangentteja. Täydennetään kuvaa piirtämällä säteet kaaren päätepisteisiin sekä merkitsemällä kaarta vastaavaa keskuskulmaa kirjaimella $\beta$.

Tangenttikulman ja sitä vastaavan keskuskulman summa on $180^{\circ}$, joten $\beta=180^{\circ}-40^{\circ}=140^{\circ}$. (1 p.)
Kaaren pituus on $b=\frac{140^{\circ}}{360^{\circ}}\cdot 2\cdot \pi \cdot 2=4{,}88\ldots\approx4{,}9$. (Lauseke oikein (1 p.), vastaus (1 p.))
b) Hahmotellaan mallikuva. (1 p.)
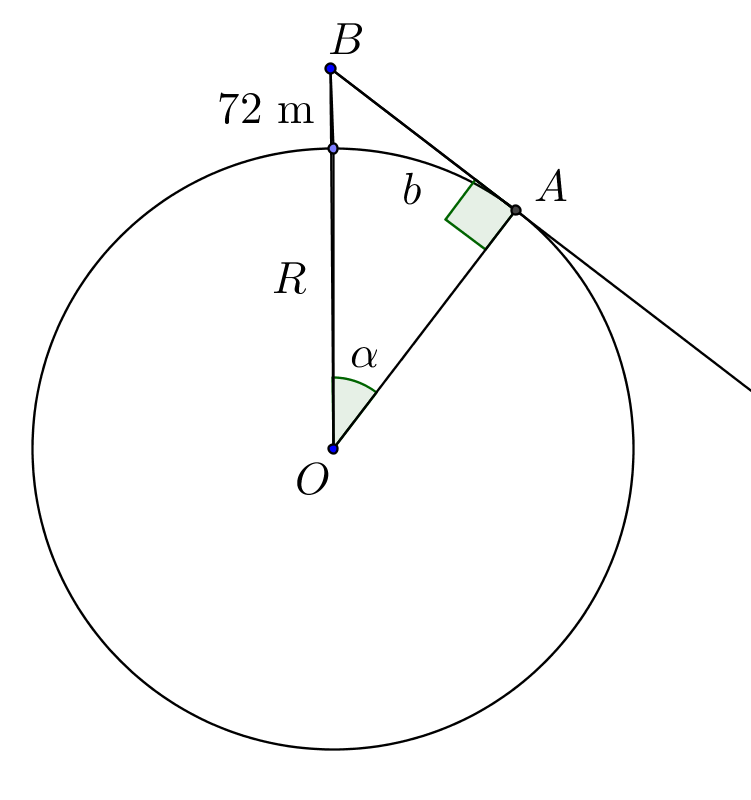
Maapallon säde on $R=6370$ km. Kun kuvan kulma $\alpha$ saadaan selvitettyä, niin tämän avulla saadaan laskettua kysytty kaaren pituus $b$. Muutetaan ensin $72$ m kilometreiksi. $72 \text{ m}=0{,}072 \text{ km}$. Suorakulmaisesta kolmiosta $OAB$ saadaan yhtälö
\(\begin{align*} \cos \alpha&=\frac{R}{R+0{,}072}\\ \cos \alpha&=\frac{6370}{6370{,}072}\\ \alpha&=0{,}272\ldots^{\circ}. \end{align*}\) (1 p.)
Kysytty etäisyys on kuvaan merkitty kaaren pituus $b$, joka on $$b=\frac{0{,}272\ldots^{\circ}}{360^{\circ}}\cdot 2\pi\cdot 6370=30{,}28\ldots \approx 30 \text{ (km)}.$$
Vastaus: Stadionin tornista voi nähdä 30 km päähän. (1 p.)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
