Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.
a) Tutki alla olevien liukukytkimien avulla yhtälön $y=kx+b$ kuvaajan muotoa muuttujien $k$ ja $b$ eri lukuarvoilla. Kuvaile sanallisesti, miten muuttujien $k$ ja $b$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin.
b) Ratkaise graafisesti (katsomalla kuvaajasta) yhtälö $-2=-2x+2$.
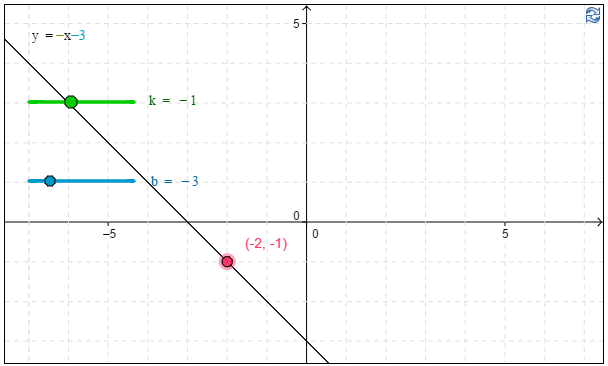
c) Määritä kuvaajan avulla lausekkeen $-x-3$ arvo, kun $x=-2$.
a)
- Muotoa $y=kx+b$ olevan yhtälön kuvaaja on suora.
- Ensimmäisen asteen termin kerroin $k$ (jota kutsutaan kulmakertoimeksi) vaikuttaa suoran "jyrkkyyteen". Kun $k>0$, suora on nouseva suora, ja kun $k<0$, suora on laskeva suora. \(\require{color}\color{red}{\text{(+1p)}}\)
- Vakiotermi $b$ vaikuttaa siihen, millä "korkeudella" suora on. Havaitaan, että suora leikkaa $y$-akselin aina pisteessä$(0,b)$. \(\require{color}\color{red}{\text{(+1p)}}\)
b) Kuvaajan avulla havaitaan, että yhtälön $-2=-2x+2$ ratkaisu on \(\underline{\underline{x =2}}\). \(\require{color}\color{red}{\text{(+2p)}}\)
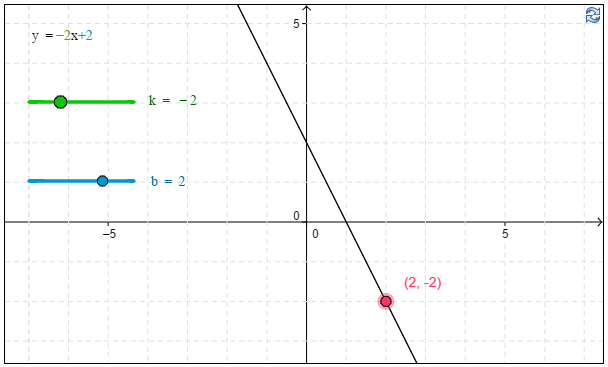
c) Kuvaajan avulla havaitaan, että \(-x-3\approx\underline{\underline{-1}}\), kun $x=-2$. \(\require{color}\color{red}{\text{(+2p)}}\)
a) Tutki alla olevien liukukytkimien avulla yhtälön $y=ax^2+bx+c$ kuvaajan muotoa muuttujien $a$, $b$ ja $c$ eri lukuarvoilla. Kuvaile sanallisesti, miten muuttujien $a$, $b$ ja $c$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin?
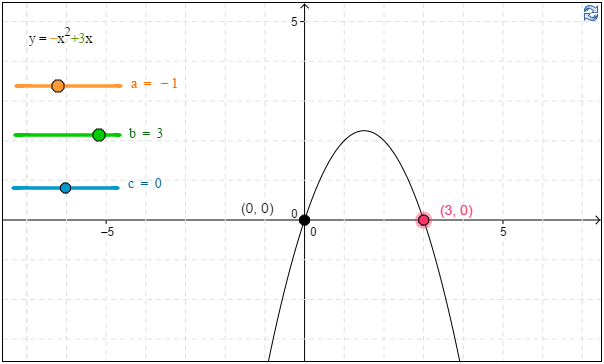
b) Ratkaise graafisesti (katsomalla kuvaajasta) yhtälö $0=-x^2+3x$.
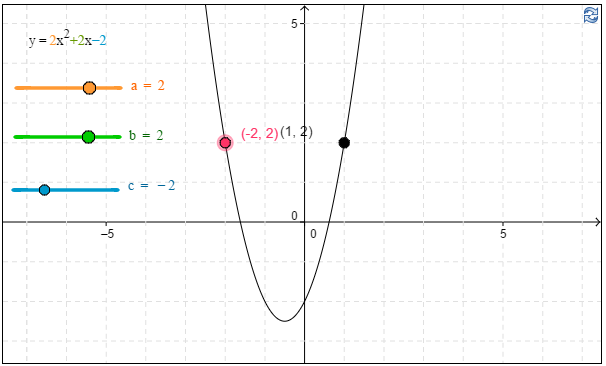
c) Määritä kuvaajan avulla lausekkeen $2x^2+2x-2$ arvo, kun $x=-2$.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a)
- Muotoa $y=ax^2+bx+c$ olevan yhtälön kuvaaja on paraabeli.
- Toisen asteen termin kerroin $a$ vaikuttaa paraabelin aukeamissuuntaan. Kun $a>0$, paraabeli on ylöspäin aukeava, ja kun $a<0$, paraabeli on alaspäin aukeava. \(\require{color}\color{red}{\text{(+1p)}}\)
- Ensimmäisen asteen termin kerroin $b$ vaikuttaa paraabelin sijaintiin sekä pysty- että sivusuunnassa. Vakiotermi $c$ vaikuttaa paraabelin sijaintiin vain pystysuunnassa. \(\require{color}\color{red}{\text{(+1p)}}\)
- Havaitaan, että paraabeli leikkaa $y$-akselin aina pisteessä$(0,c)$.
b) Kuvaajan avulla havaitaan, että yhtälön $0=-x^2+3x$ ratkaisu on \(\underline{\underline{x \approx 0}}\) tai \(\underline{\underline{x \approx 3}}\). \(\require{color}\color{red}{\text{(+2p)}}\)
c) Kuvaajan avulla havaitaan, että \(2x^2+2x-2\approx\underline{\underline{\ 2\ }}\), kun $x=-2$. \(\require{color}\color{red}{\text{(+2p)}}\)
Ratkaise yhtälö
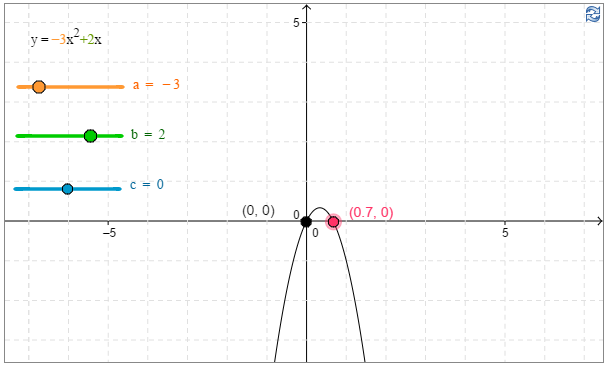
a) \(-3x^2=-2x\)
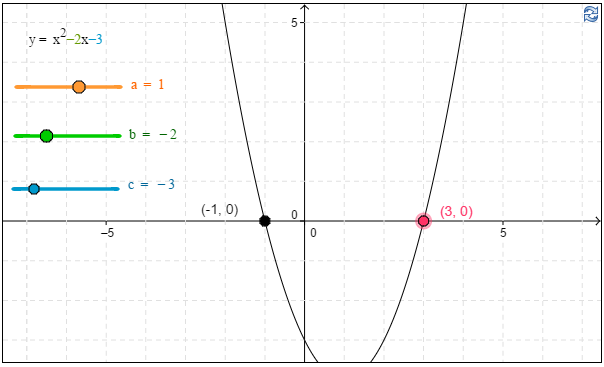
b) \(x^2-2x-3=0\)
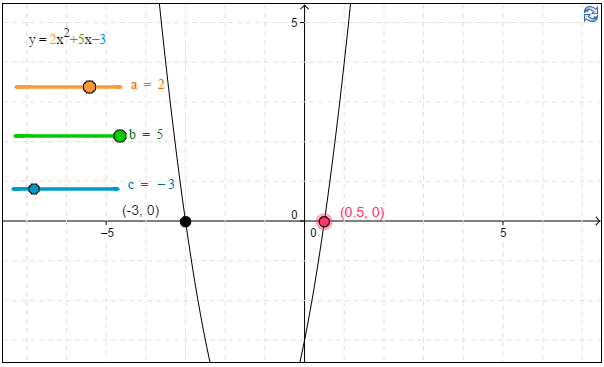
c) \(2x^2=-5x+3\)
Voit tarkistaa vastauksesi alla olevan kuvaajan avulla:
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
\( \require{color} \begin{align*} \textbf{a)}\qquad \quad -3x^2&=-2x \\ -3x^2 +2 x&=0 \\ x(-3x+2)&=0 &&||\text{ TNS = tulon nollasääntö} \\ & &&\color{red}{\text{(+1p TNS tai ratkaisukaava)}}\\ x=0 \text{ tai } &-3x+2=0 \\ \\ x=0 \text{ tai } &x=\dfrac{2}{3} \end{align*}\)
Vastaus: \(x=0\) tai \(x=\dfrac{2}{3}\). \(\require{color}\color{red}{\text{(+1p)}}\)
\( \require{color} \begin{align*} \textbf{b) }\ &x^2-2x-3=0 & &\Big|\Big|x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\\ & && \Big|\Big| a=1, b=-2, c=-3 \end{align*}\)
\( \require{color} \begin{align*} x&=\dfrac{-(-2) \pm \sqrt{(-2)^2 -4 \cdot 1 \cdot (-3)}}{2 \cdot 1} \qquad \color{red} \text{(+1p)} \\ x&=\dfrac{2 \pm \sqrt{16}}{2} \\\\ x&=\dfrac{2 \pm 4}{2} \\\\ x&=\underline{\underline{3}} \text{ tai } x=\underline{\underline{-1}} \qquad\qquad \qquad \qquad \qquad \color{red}{\text{(+1p)}} \end{align*}\)
\( \require{color} \begin{align*} \textbf{c) }2x^2&=-5x+3 &&|| +5x-3 \\ 2x^2&+5x-3=0 &&\Big|\Big|x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a} \\ \ & &&\Big|\Big|a=2, b=5, c=-3 \end{align*}\)
\( \require{color} \begin{align*} x&=\dfrac{-5 \pm \sqrt{5^2-4 \cdot 2 \cdot (-3)}}{2 \cdot 2} && \color{red} \text{(+1p)} \\ x&=\dfrac{-5 \pm \sqrt{49}}{4} \\ x&=\dfrac{-5 \pm 7}{4} \\ x&=\dfrac{2}{4}=\underline{\underline{\dfrac{1}{2}}} \text{ tai } x=\dfrac{-12}{4}=\underline{\underline{-3}} && \color{red} \text{(+1p)} \end{align*}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
