Tämä testi mittaa osaamistasi tasaisen ja muuttuvan liikkeen mallin tunnistamisesssa sekä molempiin liiketiloihin liittyvien suureyhtälöiden käytössä.
Jai alai -nimisessä pallopelissä pallon nopeus sen kimmotessa seinästä voi olla jopa 300 km/h.
Arvioi kuinka kaukana seinästä pelaajan pitää vähintään olla, jotta hän ehtisi reagoida häntä kohti tulevaan palloon?
Ihmisen reaktioaika näköhavainnon jälkeen on noin 0,20 s.
Kirjataan lähtöarvot
\(t_{min}=0,20 \text{ s}, \ v=300 \text{ km/h}\)
Oletetaan, että palloon kohdistuva ilmanvastus on mitätön.\(\quad \color{red}{\text{(+1p)}}\)
Pallo on tasaisessa liikkeessä vaakasuunnassa ja kappaleen paikka saadaan kaavasta \(\quad \color{red}{\text{(+1p)}}\)
\(x=vt\)\(\quad \color{red}{\text{(+1p)}}\)
Lasketaan pelaajan vähimmäisetäisyys seinästä.
\(x=\dfrac{300}{3,6} \text{ m/s} \cdot 0,20 \text{ s} \)\(\quad \color{red}{\text{(+1p)}}\)
\(x\approx 16,67 \text{ m}\)\(\quad \color{red}{\text{(+1p)}}\)
Vastaus: Pelaajan tulisi olla vähintään 17 metrin päässä seinästä, jotta hän ehtisi reagoida kimpoavaan palloon. \(\quad \color{red}{\text{(+1p)}}\)
Rullaluistelija saapuu kaltevan tason yläpäähän nopeudella \(2,0 \text{ m/s}\) ja laskee alas tasoa kiihtyvyydellä \(1,2 \text{ m/s}^2\).
Jos taso on \(25 \text{ m}\) pitkä, niin kuinka kauan aikaa lautailijalta kuluu rampin alapäähän?
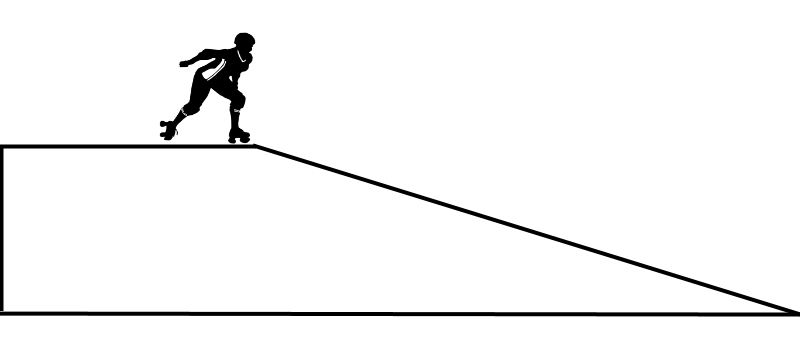
Kirjataan lähtöarvot ylös.
\(v_0=2,0 \text{ m/s}, \ a=1,2 \text{ m/s}^2\)
Rullaluistelija on tasaisesti kiihtyvässä liikkeessä. \(\quad \color{red}{\text{(+1p)}}\)
Kappaleen kulkema matka tasaisesti kiihtyvässä liikkeessä
\(s=v_0t+\dfrac{1}{2}at^2\) \(\quad \color{red}{\text{(+1p)}}\)
\(\dfrac{1}{2}at^2+v_0t-s=0\)
Ratkaistaan paikan yhtälöstä aika \(t\) toisen asteen yhtälön ratkaisukaavan avulla.
\(t=\dfrac{-v_0 \pm \sqrt{v_o^2-4\cdot \frac{1}{2}a \cdot (-s)}}{2 \cdot \frac{1}{2}a}\)\(\quad \color{red}{\text{(+1p)}}\)
\(t= \dfrac{-2,0 \frac{\text{m}}{\text{s}}\pm \sqrt{(2,0 \frac{\text{m}}{\text{s}})^2-2 \cdot 1,2 \frac{\text{m}}{\text{s}^2} \cdot(- 25 \text{ m})}}{1,2 \frac{\text{m}}{\text{s}^2}}\)\(\quad \color{red}{\text{(+1p)}}\)
\(\underline{\underline{t_1 = 5,0 \text{ s ja } x_2 \approx -8,3 \text{ s}}}\) \(\quad \color{red}{\text{(+1p)}}\)
Hylätään negatiivinen vaihtoehto, koska tapahtumaan kulunut aika on aina positiivista.
Vastaus: Rullaluistelijalta kuluu rampin laskemiseen 5,0 s.. \(\quad \color{red}{\text{(+1p)}}\)
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Oheisessa kuvaajassa on erään kappaleen nopeus ajan funktiona.
Oranssista napista pystyt valitsemaan haluatko piirtää käyrälle sekantin vai tangentin.
Selvitä kuvaajan avulla
a) Kappaleen keskikiihtyvyys välillä 0,0 s ... 1,5 s.
b) Hetkellinen kiihtyvyys, kun t = 3,5 s
a) Piirretään kuvaajalle ajanhetkien \(t=0,0 \text{ s}\) ja \(t=1,5 \text{ s}\) kautta suora.
Suoran fysikaalinen kulmakerroin kuvaa kappaleen keskikiihtyvyyttä välillä \(0,0 \text{ s} \ldots 1,5 \text{ s}\). \(\require{color}\color{red}{\text{(+1p)}}\)
\(\require{color}\color{red}{\text{(Suora piirretty oikeiden pisteiden kautta +1p)}}\)
\(a_k=\dfrac{\Delta v}{\Delta t}=\dfrac{1,7 \text{ m/s}-0,0 \text{ m/s}}{1,5 \text{ s} - 0,0 \text{s}} \approx \underline{\underline{ 1,1 \text{ m/s}^2}}\)\(\require{color}\color{red}{\text{(+1p)}}\)
b) Piirretään kuvaajalle tangentti ajanhetkeen \(t=3,5 \text{ s}\).
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
