Täm testi mittaa osaamistasi Newtonin lakien, voimien komponenttien sekä liikeyhtälön käytössä.
Ovatko seuraavat väittämät Newtonin lakien mukaisia? Perustele.
a) Pöydällä levossa olevaan omenaan ei kohdistu voimia.
b) Polttoaineen loputtua, kaukana kaikista taivaankappaleista avaruusalus jatkaa matkaansa muuttumattomalla nopeudella.
c) Kuu vetää Maata puoleensa pienemmällä voimalla, kuin Maa kuuta.
a) Väite on epätotta. \(\color{Red}{\text{(+1p)}}\)
Pöydällä olevaan omenaan kohdistuu voimista ainakin
- paino G, joka aiheutuu maan vetovoimasta.\(\color{Red}{(+\frac{1}{2}\text{p})}\)
- pöytän tukivoima N.\(\color{Red}{(+\frac{1}{2}\text{p})}\)
(Huom! Kyseiset voimat eivät ole voima-vastavoima pari, koska kohdistuvat samaan kappaleeseen.)
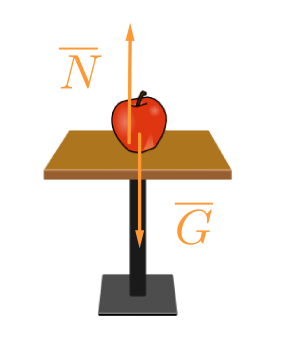
Omenaan kohdistuvien voimien summa on nolla (\(\sum \overline{F}=\overline{0}\)), joten omena on levossa Newtonin 2. lain mukaisesti.
b) Väite on totta. \(\color{Red}{\text{(+1p)}}\)
Newtonin 1. lain mukaan kappale jatkaa tasaista liikettä jos siihen ei vaikuta ulkoisia voimia. \(\color{Red}{\text{(+1p)}}\)
(Huom! Gravitaatiovuorovaikutuksen voimakkuus heikkenee etäisyyden kasvaessa \(F \sim \dfrac{1}{r^2}\))
c) Väite on epätotta. \(\color{Red}{\text{(+1p)}}\)
Newtonin 3. lain mukaan Maa ja Kuu vetävät toisiaan puoleensa yhtä suurilla, mutta vastakkaissuuntaisilla voimilla. \(\color{Red}{\text{(+1p)}}\)
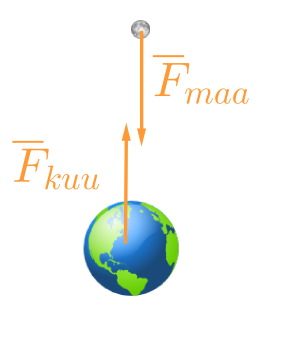
(Huom! Maan ja Kuun massat kuitenkin eroavat, joten voimien vaikutukset ovat kappaleilla erilaiset)
Aikuinen mies istuu leikkipuiston keinussa. Kuinka suuri vaakasuuntainen voima pitäisi keinuun
kohdistaa, että keinu muodostaisi 30 asteen kulman pystysuunnan kanssa? Miehen massa on 80 kg.

Kirjataan lähtoarvot ylös \(\alpha=30^{\circ}, \ m=80 \text{ kg}\)
Piirretään kuvio, johon merkitään keinuun kohdistuvat voimat.
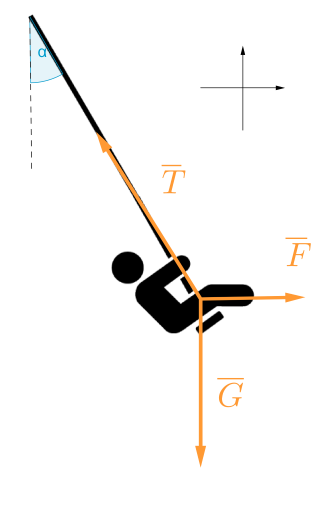
\(\color{Red}{\text{(Kuvasta, jossa voimat oikeassa suhteessa +1p)}}\)
Koska kappale on tasapainossa etenemisen suhteen, niin dynamiikan peruslain mukaan \(\sum \overline{F}=\overline{0}\) \(\color{Red}{\text{( +1p)}}\)
Tapa 1. Piirretään voimakuvio
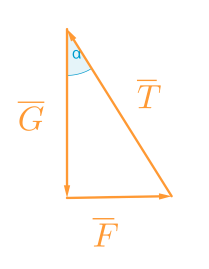 \(\color{Red}{\text{( +1p)}}\)
\(\color{Red}{\text{( +1p)}}\)
Voimakuviosta huomataan, että
\(\tan \alpha = \dfrac{F}{G}\) \(\color{Red}{\text{( +1p)}}\)
\(F=G \tan \alpha\)
\(F = mg \tan \alpha\)
\(F=80 \text{ kg} \cdot 9,81 \text{ m/s}^2\cdot \tan 30^{\circ}\)\(\color{Red}{\text{( +1p)}}\)
\(F \approx 453 \text{ N}\)
Tapa 2. Kompponentteihin jako
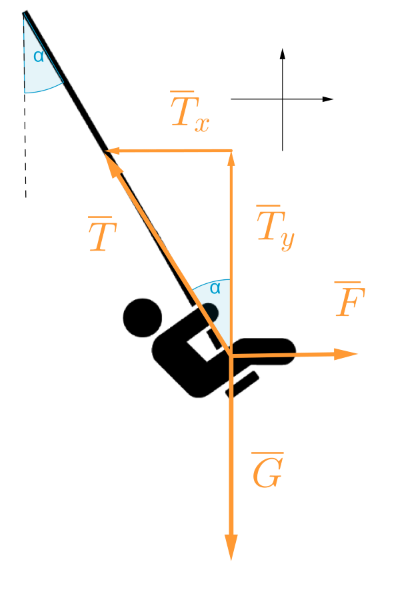
Jaetaan voimatarkastelu x- ja y-suuntiin.
y-suunta.
\(\sum \overline{F}_y=\overline{0} \\ \overline{G}+\overline{T}_y=\overline{0}\)
\(-G+T \cos \alpha=0\)
\(T=\dfrac{mg}{\cos \alpha}\) \(\color{Red}{\text{( +1p)}}\)
x-suunta
\(\sum \overline{F}_x=\overline{0}\)
\(\overline{T}_x+\overline{F}=\overline{0}\)
\(- T_x + F =0\)
\(F = T \sin \alpha\)\(\ \qquad \qquad || T = \dfrac{mg}{\cos \alpha}\)
\(F= \dfrac{mg}{\cos \alpha} \cdot \sin \alpha\)\( \qquad || \frac{\sin \alpha}{\cos \alpha}=\tan \alpha\) \(\color{Red}{\text{( +1p)}}\)
\(F=mg \tan \alpha\)
\(F=80 \text{ kg} \cdot 9,81 \text{ m/s}^2\cdot \tan 30^{\circ}\) \(\color{Red}{\text{( +1p)}}\)
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Laatikkoa, jonka massa on 2,0 kg, liikkeelle lähtöä tutkittiin voima-anturin avulla.
Paina oranssia nappia, niin näet millainen kuvaaja syntyi (t, F)-koordinaatistoon.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
Liikkeelle lähdön jälkeen laatikon liike on lähes tasaista.
a) Selvitä (t, F) -kuvaajan muoto (2p).
b) Kuinka suuri on lähtökitka? (1p).
c) Laske laatikon ja lattian välinen liukukitkakerroin (3p).
a) \(0,0 \text{ s} \ldots 4,0 \text{ s}\)
Lepokitka kasvaa vetävän voiman \(F\) kasvaessa, \(\quad \color{red}{(+\frac{1}{2}\text{p})}\)
kunnes lepokitka saavuttaa suurimman arvonsa, lähtökitkan \(F_{\mu0}\). \(\quad \color{red}{(+\frac{1}{2}\text{p})}\)
Tämän jälkeen laatikko lähtee liikkeelle.
\(4,0 \text{ s} \ldots 10,0 \text{ s}\)
Laatikon ja lattian välinen liukukitka \(F_\mu\) on pienempi kuin lähtökitka \(F_{\mu0}\), \(\quad \color{red}{(+\frac{1}{2}\text{p})}\)
joten laatikon tasaisen liikkeen ylläpitämiseen tarvittava vetävä voima \(F\) on pienempi kuin
liikkeelle lähtöön tarvittava voima. Koska laatikko on tasaisessa liikkeessä,
niin \(F=F_\mu\) eli \(F\) on vakio. \(\quad \color{red}{(+\frac{1}{2}\text{p})}\)
b)
Kuvaajasta saadaan luettua lähtökitka, joka on noin \(\underline{\underline{F_{\mu0} \approx 6,0 \ \text{N}}}\)\(\quad \color{red}{(+1\text{p})}\)
c) Kirjataan lähtöarvot \(m=2,0 \text{ kg}, \ g = 9,81 \text{ m/s}^2\) .
Piirretään kuva, johon merkitään laatikkoon kohdistuvat voimat, kun laatikko on tasaisessa liikkeessä.
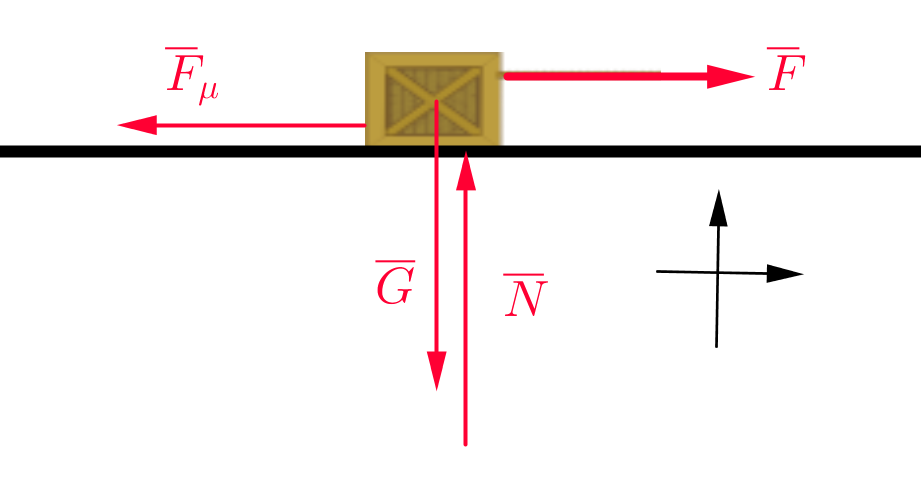
Koska kappale on tasaisessa liikkeessä, niin Dynamiikan peruslain mukaan \(\underline{\sum \overline{F}=\overline{0}}\)\(\quad \color{red}{(+1\text{p})}\)
y-suunnassa
\(\sum \overline{F}_y=\overline{0} \\ \overline{G}+\overline{N}=\overline{0} \\ N=mg\)
x-suunnassa
\(\sum \overline{F}_x=\overline{0}\)
\(\overline{F}+\overline{F}_{\mu}=\overline{0}\)
\(F_\mu = F \qquad || F_\mu = \mu N \)
\(\mu N = F \qquad || N = mg\)
\(\mu mg = F\)
\(\mu = \dfrac{F}{mg}\) \(\quad \color{red}{(+1\text{p})}\)
Kuvaajasta luetaan, että kun laatikko on tasaisessa liikkeessä niin vetävä voima on noin \(F \approx 4,0 \text{ N}\)
\(\mu = \dfrac{4,0 \text{ N}}{2,0 \text{ kg} \cdot 9,81 \frac{\text{m}}{\text{s}^2}}\)
\(\underline{\underline{\mu \approx 0,20}}\) \(\quad \color{red}{(+1\text{p})}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
