Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.
a) Ratkaise graafisesti (kuvaajasta) ja algebrallisesti (laskemalla) epäyhtälö $-2x+4>0$.
b) Ratkaise epäyhtälö $4x+6 \le 2x-5$.
c) Ratkaise epäyhtälö $x+3(x+3) \ge 4(x-2)+5$
a) Graafisesti: kuvaajan perusteella vastaus on \(\underline{\underline{x<2}}\). \(\require{color}\color{red}{\text{(+1p)}}\)
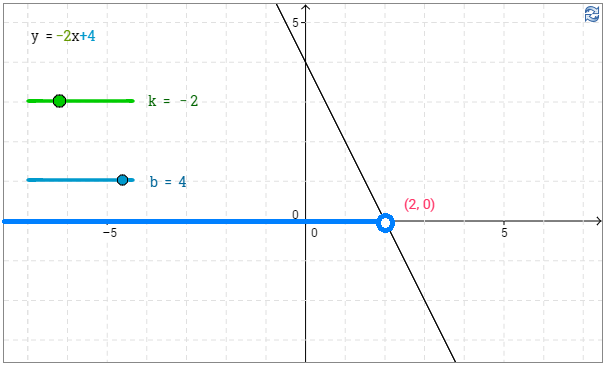
Laskemalla:
\(\begin{align*}-2x+4&>0 &&||-4 \\ -2x&>-4 &&||:(-2) <0 \\ \frac{-2x}{-2}&<\frac{-4}{-2} \\ x&<2 && \require{color}\color{red}{\text{(+1p)}} \end{align*}\)
\(\begin{align*} \textbf{b) } 4x+6 &\le 2x-5 &&||-2x \\ 2x+6 &\le -5 &&||-6\\ 2x& \le-11&&||:2>0 \qquad\require{color}\color{red}{\text{(+1p)}} \\ x &\le -\frac{11}{2} \end{align*}\)
Vastaus: $x \le -\frac{11}{2}$. \(\require{color}\color{red}{\text{(+1p)}}\)
\(\begin{align*} \textbf{c) } x+3(x+3)& \ge 4(x-2)+5 \\ x+3x+9&\ge 4x-8+5\\4x+9&\ge4x-3 &&||-4x\\ 9& \ge-3 &&\require{color}\color{red}{\text{(+1p)}} \end{align*}\)
Vastaus: Epäyhtälön toteuttavat kaikki reaaliluvut. \(\require{color}\color{red}{\text{(+1p)}}\)
a) Ratkaise graafisesti epäyhtälö $-x^2+2x+3 \ge 0$.
b) Määritä graafisesti, millä muuttujan arvoilla funktion $f(x)=2x^2-4x$ arvot ovat positiivisia.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a) Ratkaistaan, millä muuttujan arvoilla funktion $-x^2+2x+3$ arvot ovat positiivisia tai nolla. Kuvaajasta nähdään, että kyseessä on alaspäin aukeava paraabeli, jonka nollakohdat ovat $x=-1$ ja $x=3$. \(\require{color}\color{red}{\text{(+1p)}}\)
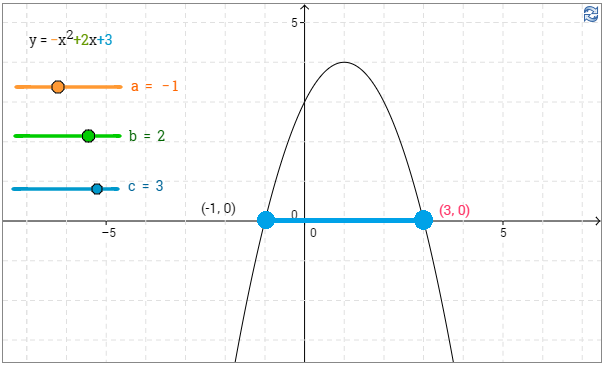
Funktion arvot ovat positiivisia $x$-akselin yläpuolella, eli tässä tapauksessa funktion nollakohtien välissä. \(\require{color}\color{red}{\text{(+1p)}}\)
Vastaus: $-1 \le x \le 3$. \(\require{color}\color{red}{\text{(+1p)}}\)
b) Kuvaajasta nähdään, että kyseessä on ylöspäin aukeava paraabeli, jonka nollakohdat ovat $x=0$ ja $x=2$. \(\require{color}\color{red}{\text{(+1p)}}\)
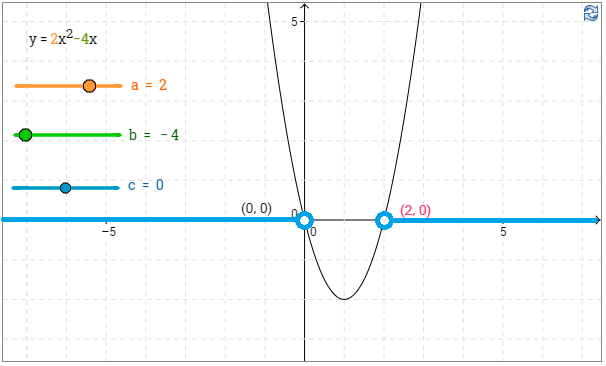
Funktion arvot ovat positiivisia $x$-akselin yläpuolella, eli tässä tapauksessa nollakohtien ulkopuolella. \(\require{color}\color{red}{\text{(+1p)}}\)
Vastaus: $x<0$ tai $x>2$. \(\require{color}\color{red}{\text{(+1p)}}\)
Ratkaise epäyhtälö
a) \(-3x^2 \le -2x\)
b) \(2x^2<-5x+3\)
Ratkaise laskemalla, mutta voit hahmotella tilannetta alla olevan kuvaajan avulla:
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
\( \require{color} \begin{align*} \textbf{a)}\qquad -3x^2&\le-2x \\ -3x^2 +2 x&\le0 \end{align*}\)
Tutkitaan, millä muuttujan arvoilla funktion $-3x^2+2x$ arvot ovat negatiivisia tai nolla. Toisen asteen termin kerroin on negatiivinen, joten funktion kuvaaja on alaspäin aukeava paraabeli. \(\require{color}\color{red}{\text{(+1p)}}\)
Ratkaistaan funktion nollakohdat:
\( \require{color} \begin{align*} -3x^2 +2 x&=0 \\ x(-3x+2)&=0 &&||\text{ tulon nollasääntö} \\\\\ x=0 \text{ tai } &-3x+2=0 \\ \\ x=0 \text{ tai } &x=\dfrac{2}{3} &&\require{color}\color{red}{\text{(+1p)}} \end{align*}\)
Funktion arvot ovat negatiivisia $x$-akselin alapuolella, eli tässä tapauksessa nollakohtien ulkopuolella.
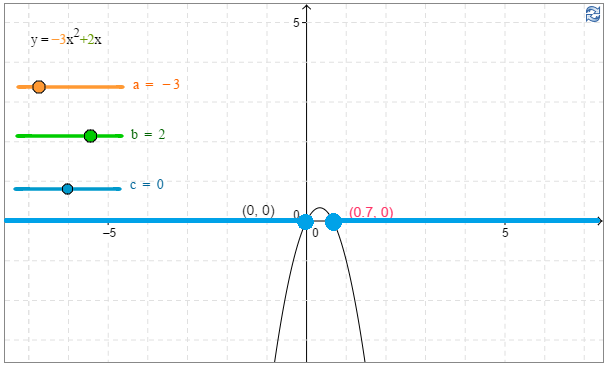
Vastaus: \(x\le0\) tai \(x\ge\dfrac{2}{3}\). \(\require{color}\color{red}{\text{(+1p)}}\)
\( \require{color} \begin{align*} \textbf{b)}\qquad \qquad \quad2x^2&<-5x+3 &&|| +5x-3 \\ 2x^2+5x-3&<0 \end{align*}\)
Tutkitaan, millä muuttujan arvoilla funktion $2x^2+5x-3$ arvot ovat negatiivisia. Toisen asteen termin kerroin on positiivinen, joten funktion kuvaaja on ylöspäin aukeava paraabeli. \(\require{color}\color{red}{\text{(+1p)}}\)
Ratkaistaan funktion nollakohdat:
\( \require{color} \begin{align*} 2x^2&+5x-3=0 &&\Big|\Big|x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a} \\ \ & &&\Big|\Big|a=2, b=5, c=-3 \end{align*}\)
\( \require{color} \begin{align*} x&=\dfrac{-5 \pm \sqrt{5^2-4 \cdot 2 \cdot (-3)}}{2 \cdot 2} \\ x&=\dfrac{-5 \pm \sqrt{49}}{4} \\ x&=\dfrac{-5 \pm 7}{4} \\\\ x&=\dfrac{2}{4}=\dfrac{1}{2} \quad \text{tai} \quad x=\dfrac{-12}{4}=-3 && \color{red} \text{(+1p)} \end{align*}\)
Funktion arvot ovat negatiivisia $x$-akselin alapuolella, eli tässä tapauksessa nollakohtien välissä.
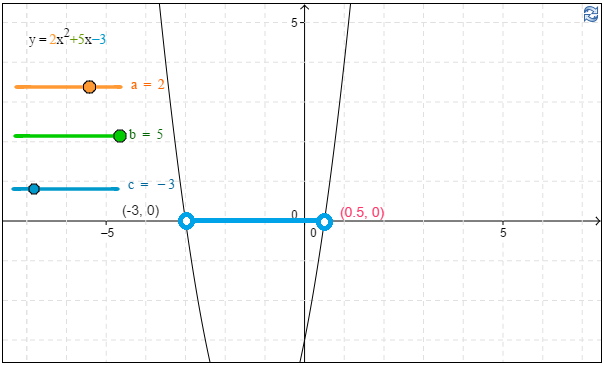
Vastaus: \(-3<x<\dfrac12\). \(\require{color}\color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
