(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Tutki alla olevien liukukytkimien avulla funktion $f(x)=ax^2+bx+c$ kuvaajan muotoa muuttujien $a$, $b$ ja $c$ eri lukuarvoilla.
a) Kuvaile sanallisesti, miten muuttujien $a$, $b$ ja $c$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin.
b) Ratkaise graafisesti (liikuttamalla punaista pistettä käyrällä) yhtälö $4=2x^2−0,5x−3$.
c) Määritä graafisesti $f(1)$, kun $f(x)=−x^2+2x+3$.
a)
- Muotoa $f(x)=ax^2+bx+c$ olevan funktion kuvaaja on paraabeli.
- Toisen asteen termin kerroin a vaikuttaa paraabelin aukeamissuuntaan. Kun $a>0$, paraabeli on ylöspäin aukeava, ja kun $a<0$, paraabeli on alaspäin aukeava. $\color{Red}{(+1p)}$
- Ensimmäisen asteen termin kerroin b vaikuttaa paraabelin sijaintiin sekä pysty- että sivusuunnassa. Vakiotermi $c$ vaikuttaa paraabelin sijaintiin vain pystysuunnassa. $\color{Red}{(+1p)}$
- Havaitaan, että paraabeli leikkaa y-akselin aina pisteessä $(0,c)$.
b) Kuvaajan avulla havaitaan, että yhtälön $4=2x^2−0,5x−3$ ratkaisu on $x \approx 1,8$ tai $x\approx 2$. $\color{Red}{(+2p)}$
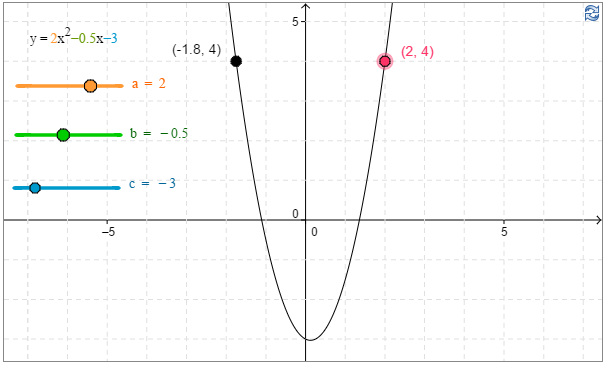
c) Kuvaajan avulla havaitaan, että funktion $f(x)=−x^2+2x+3$ arvo $f(1)\approx 4$. $\color{Red}{(+2p)}$
Olkoon funktio $f(x)=2x^2-5x+2$.
a) Laske funktion $f$ arvo, kun $x=-\frac{1}{2}$.
b) Ratkaise, millä $x$:n arvoilla $f(x)=14$.
c) Tutki alla olevan sovelluksen avulla, missä pisteissä $f$ leikkaa koordinaattiakselit.
d) Ratkaise laskemalla, missä pisteissä $f$ leikkaa koordinaattiakselit.
a)
\(\begin{align} f(-\frac{1}{2})&=2\cdot (-\frac{1}{2})^2-5\cdot (-\frac{1}{2})+2 \\ &= 2\cdot \frac{1}{4}+\frac{5}{2}+2 \\ &= \frac{2}{4}+ ^{2)}\frac{5}{2}+2 \\ &=\frac{2+10}{4}+2 \\ &= 3+2 \\ &= 5 \end{align}\)$\color{Red}{(+1p)}$
b) Ratkaistaan yhtälö
\(\begin{align} 2x^2-5x+2&=14\\ 2x^2-5x-12&= 0 \end{align}\)
\(\begin{align} x &= {-(-5) \pm \sqrt{(-5)^2-4\cdot 2 \cdot (-12)} \over 2\cdot 2} \\ &= \frac{5 \pm \sqrt{25 + 96}}{4} \\ &= \frac{5 \pm \sqrt{121}}{4} \\ &= \frac{5 \pm 11}{4} \end{align}\)
\(\begin{array}{rclrcl} x&=&\frac{5+11}{4}&\text{ tai }& x&=&\frac{5-11}{4} \\ &=&4 && &=&-\frac{3}{2} \end{array}\)$\color{Red}{(+1p)}$
c)
$x$-akselin leikkauspisteet ovat $(\frac{1}{2},0)$ ja $(2,0)$.
$y$-akselin leikkauspiste on $(0,2)$. $\color{Red}{(+1p)}$
d) $x$-akselin leikkauspisteissä $f(x)=0$:
\(\begin{align} x &= {-(-5) \pm \sqrt{(-5)^2-4\cdot 2 \cdot 2} \over 2\cdot 2} \\ &=\frac{5 \pm \sqrt{25-16}}{4} \\ &= \frac{5\pm \sqrt{9}}{4} \\ &= \frac{5\pm 3}{4} \end{align}\)
\(\begin{array}{rclrcl} x&=&\frac{5+3}{4} & \text{tai} & x&=&\frac{5-3}{4} \\ &=&2 &&&=&\frac{1}{2} \end{array}\)$\color{Red}{(+1p)}$
Funktio leikkaa $y$-akselin, kun $x=0$:
$f(0)=2\cdot 0^2 - 5\cdot 0 + 2 =2$ $\color{Red}{(+1p)}$
Vastaus: $x$-akselin leikkauspisteet ovat $(2,0)$ ja $(\frac{1}{2},0)$ ja $y$-akselin leikkauspiste on$(0,2)$ $\color{Red}{(+1p)}$
Ratkaise epäyhtälö
a) \(−3x^2 \leq -2x\)
b) \(2x^2 < -5x+3\)
Ratkaise laskemalla, mutta voit hahmotella tilannetta alla olevan kuvaajan avulla:
a)
\(\begin{align} −3x^2&≤−2x \\ −3x^2+2x&≤0 \end{align}\)
Tutkitaan, millä muuttujan arvoilla funktion $−3x^2+2x$ arvot ovat negatiivisia tai nolla. Toisen asteen termin kerroin on negatiivinen, joten funktion kuvaaja on alaspäin aukeava paraabeli. $\color{Red}{(+1p)}$
Ratkaistaan funktion nollakohdat:
\(\begin{align} -3x^2+2x&=0 \\ x(-3x+2)&=0 \qquad || \text{ tulon nollasääntö} \\ \end{align}\)
\(\begin{array}{rclcrcl} x&=&0&\text{ tai }& -3x+2&=&0 \\ && && -3x&=&-2 & \qquad ||:(-3) \\ &&&& x &=&\frac{2}{3} \end{array}\) $\color{Red}{(+1p)}$
Funktion arvot ovat negatiivisia $x$-akselin alapuolella, eli tässä tapauksessa nollakohtien ulkopuolella.
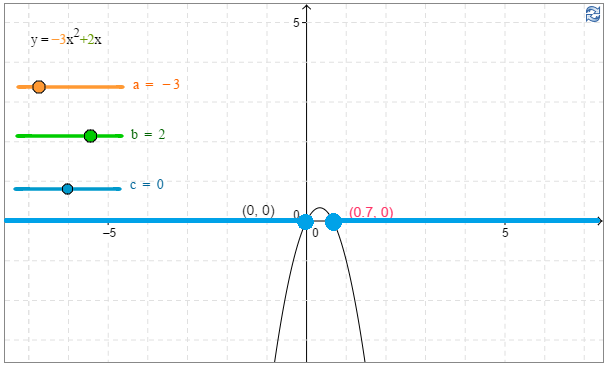
Vastaus: $x≤0$ tai $x≥\frac{2}{3}$. $\color{Red}{(+1p)}$
b)
\(\begin{align} 2x^2&<-5x+3 \\ 2x^2+5x+3&<0 \end{align}\)
Tutkitaan, millä muuttujan arvoilla funktion $2x^2+5x−3$ arvot ovat negatiivisia. Toisen asteen termin kerroin on positiivinen, joten funktion kuvaaja on ylöspäin aukeava paraabeli. $\color{Red}{(+1p)}$
Ratkaistaan funktion nollakohdat:
$2x^2+5x−3=0$
\(\begin{align} x& = {-5 \pm \sqrt{5^2-4\cdot 2 \cdot (-3)} \over 2\cdot 2} \\ &= \frac{-5\pm \sqrt{25+24}}{4}\\ &= \frac{-5\pm \sqrt{49}}{4} \\ &= \frac{-5 \pm 7}{4} \end{align}\)
\(\begin{array}{rclrcl} x&=&\frac{-5+7}{4} & \text{ tai } & x&=&\frac{-5-7}{4} \\ &=&\frac{2}{4} & & &=& \frac{-12}{4} \\ & & & & & = & -3 \end{array}\)$\color{Red}{(+1p)}$
Funktion arvot ovat negatiivisia $x$-akselin alapuolella, eli tässä tapauksessa nollakohtien välissä.
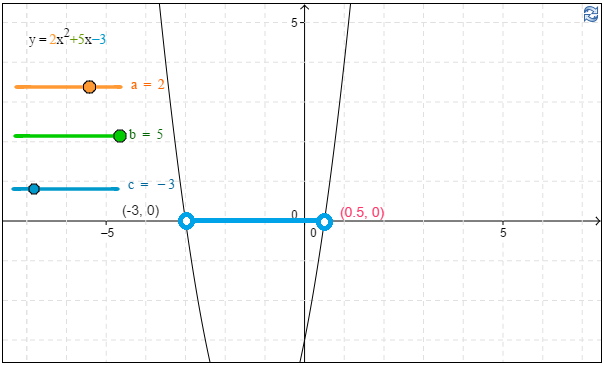
Vastaus: $−3<x<12$. $\color{Red}{(+1p)}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
