Tämä testi mittaa tietämystäsi nosteesta ja työstä.
Kuinka suuri osa jäävuoren kokonaistilavuudesta on merenpinnan alapuolella?

Taulukkokirjasta saadut lähtöarvot
\(\rho_{jää}=917 \text{ kg/m}^3 \\ \rho_{meri}=1027 \text{ kg/m}^3 \\ g=9,81 \text{ m/s}^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
Olkoon \(V\) jäävuoren kokonaistilavuus
ja \(V_{0}\) merenpinnan alapuolella oleva osa jäävuoresta.
Jäävuoreen kohdistuvat voimat ovat paino ja noste. \(\require{color}\color{red}{\text{(+1p)}}\)

Tasapainotilanteessa jäävuori on on paikoillaan
tai tasaisessa liikkeessä.
Valitaan suunta ylöspäin positiiviseksi.
Newtonin 2. lain mukaan
\(\sum \overline{F}=\overline{0}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(\overline{G}+\overline{N}=\overline{0}\)
\(-G+N=0\)
\(-mg + \rho_{meri} V_0 g=0\)
\(-\rho_{jää} V g + \rho_{meri}V_0 g=0\)
\(V_0=\dfrac{\rho_{jää}}{\rho_{meri}}V\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(V_0 = \dfrac{917 \text{ kg/m}^3}{1027 \text{ kg/m}^3}V\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(V_0 \approx 0,893 V\)
Vastaus: noin 89 prosenttia jäävuoren
kokonaistilavuudesta on merenpinnan alapuolella. \(\require{color}\color{red}{\text{(+1p)}}\)
Apollo 15 lennon aikana astronautti Davidd Scott pudotti kuun pinnalla samanaikaisesti höyhenen ja vasaran.
a) Miksi höyhen ja vasara putosivat kuun pinnalle samanaikaisesti?
b) Mitä tapahtuisi jos toistaisit kokeen maanpinnalla?
Käytä perusteluissasi apuna voimakuvioita.
a) Koska kuussa ei ole ilmakehää, niin höyheneen ja kolikkoon ei kohdistu ilmanvastusta.
Ainoa voima joka kappaleisiin kohdistuu on kuun vetovoima.
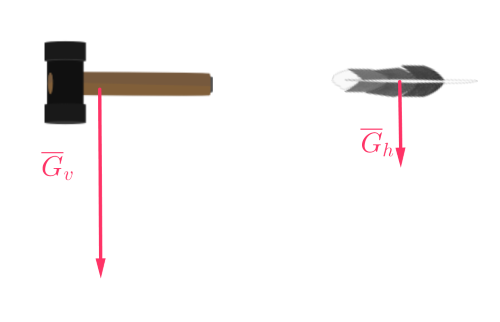 \(\require{color}\color{red}{\text{(+1p)}}\)
\(\require{color}\color{red}{\text{(+1p)}}\)
Newtonin 2. lain mukaan
\(\sum \overline{F}=m\overline{a}\)
\(\overline{G}=m\overline{a}\)
\(a=\dfrac{G}{m}\)
\(a=\dfrac{m g_{kuu}}{m}\)
\(a=g_{kuu}\) \(\require{color}\color{red}{\text{(+1p)}}\)
Molemmilla kappaleilla on sama kiihtyvyys, joten ne osuvat kuun pintaan samalla hetkellä. \(\require{color}\color{red}{\text{(+1p)}}\)
b) Maanpinnalla kappaleisiin vaikuttaa paino ja ilmanvastus.
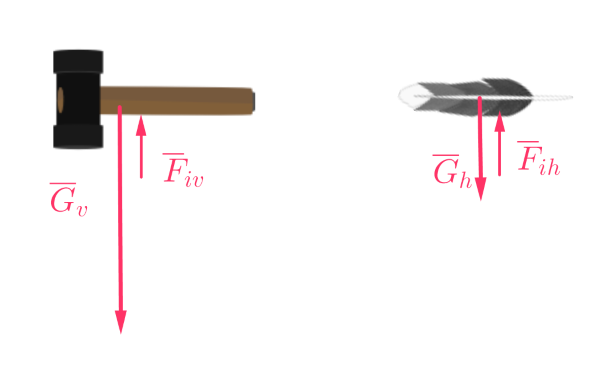 \(\require{color}\color{red}{\text{(+1p)}}\)
\(\require{color}\color{red}{\text{(+1p)}}\)
Kappaleisiin vaikuttavat ilmanvastukset ovat erisuuret.
Höyheneen vaikuttava kokonaisvoima on pienempi kuin vasaraan vaikuttava kokonaisvoima.
Tämän takia höyhenen kiihtyvyys on pienempi kuin vasaran kiihtyvyys. \(\require{color}\color{red}{\text{(+1p)}}\)
Vasara putoaa ensimmäisenä maanpintaan. \(\require{color}\color{red}{\text{(+1p)}}\)
Harvinaisen herkkäliikkeistä VW Kombi pakettiautoa työnnetään vakionopeudella rampin alapäästä yläpäähän.
Kuinka suuri työ tehdään, kun pakettiauton massa on 1700 kg ja
12 metriä pitkä ramppi muodostaa 14 asteen kulman vaakatason kanssa.

\(\sum \overline{F}=\overline{0}\)
\(\overline{F}+\overline{N}+\overline{G}=\overline{0}\) \(\require{color}\color{red}{\text{(+1p)}}\)
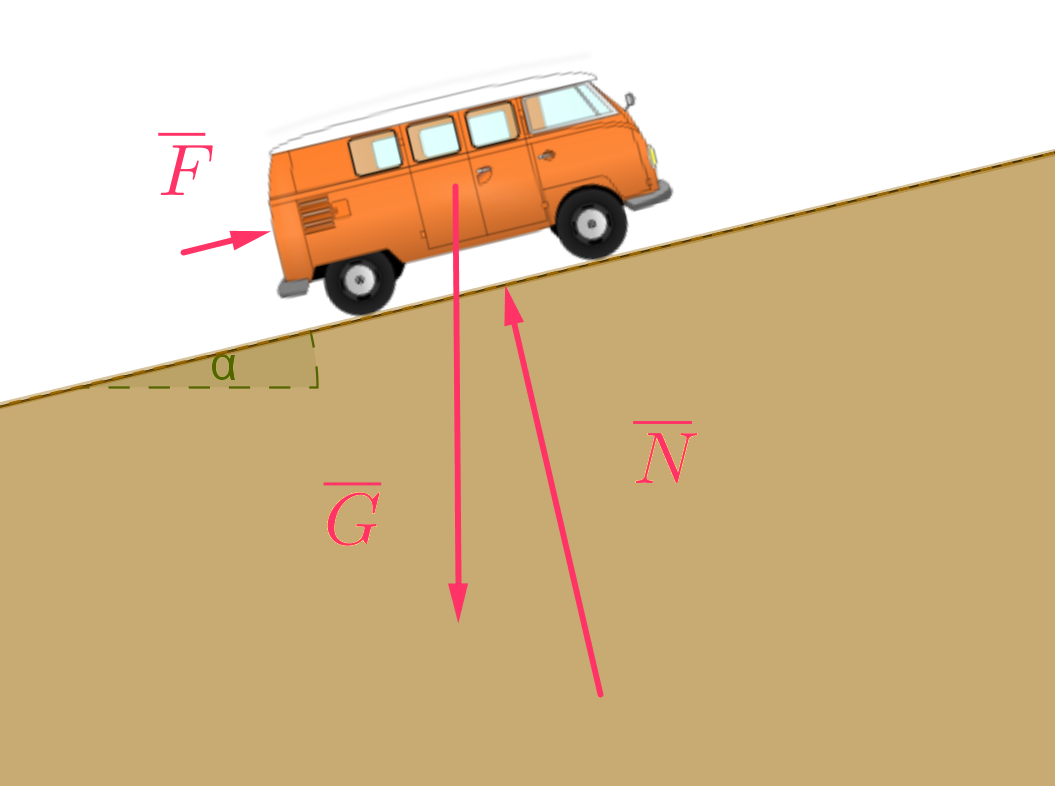
Pinnan tukivoima ja pakettiautoa työntävä voima ovat kohtisuorassa toisiinsa nähden.
Piirretään vektorikolmio, johon merkitään pakettiautoon kohdistuvat voimat.
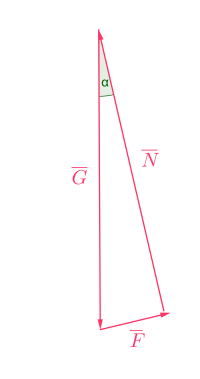 \(\require{color}\color{red}{\text{(+1p)}}\)
\(\require{color}\color{red}{\text{(+1p)}}\)
Suorakulmaisesta kolmiosta saadaan
\(\sin \alpha = \dfrac{F}{G}\)
\(F=G\sin \alpha\)
\(F=mg\sin \alpha\)\(\require{color}\color{red}{\text{(+1p)}}\)
Koska voima ja siirtymä ovat samansuuntaiset, niin voiman tekemä on
\(W=F\Delta x\)
\(W=mg \sin \alpha \cdot \Delta x\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(W=1700 \text{ kg} \cdot 9,81 \frac{\text{m}}{\text{s}^2} \cdot \sin 14^{\circ} \cdot 12 \text{ m}\)
\(W \approx 48 \ 414 \text{ J}\)
Vastaus: Tehty työ on noin 48 kJ. \(\require{color}\color{red}{\text{(+1p)}}\)
Huom! Toinen tapa tehdä tehtävä olisi komponenttitarkastelu tason ja tasoa vastaan kohtisuorassa suunnassa.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
