Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.
a) Tutki ja päättele alla olevan kuvaajan sekä ratkaisukaavan lukujen avulla, milloin toisen asteen yhtälöllä $ax^2+bx+c=0$ on kaksi ratkaisua, milloin yksi ratkaisu, ja milloin ei yhtään ratkaisua.
b) Ratkaise laskemalla, kuinka monta juurta yhtälöllä $-2x^2-2=4x$.
a) Nimetään toisen asteen yhtälön ratkaisukaavassa juurrettavana oleva lauseke $b^2-4ac$ diskriminantiksi ja merkitään sitä D-kirjaimella.
Eli $D=b^2-4ac$.
- Toisen asteen yhtälöllä on kaksi ratkaisua, kun diskriminantti on positiivinen $(D>0)$. \(\require{color}\color{red}{\text{(+1p)}}\)
- Yhtälöllä on yksi ratkaisu, kun diskriminantti on nolla $(D=0)$. \(\require{color}\color{red}{\text{(+1p)}}\)
- Kun diskriminantti on negatiivinen $(D<0)$, yhtälöllä ei ole ratkaisua. \(\require{color}\color{red}{\text{(+1p)}}\)
b)
\(\begin{align*}-2x^2-2&=4x &&||-4x \\ -2x^2-4x-2&=0 &&||a=-2, b=-4, c=-2 \end{align*}\)
Ratkaistaan juurien lukumäärä diskriminantin avulla.
\(\begin{align*}D&=b^2-4ac \\ &=(-4)^2-4 \cdot (-2) \cdot (-2) && \require{color}\color{red}{\text{(+1p)}}\\ &=16-16\\ &=0 &&\color{red}{\text{(+1p)}} \end{align*}\)
Vastaus: Koska yhtälön diskriminantti on nolla, yhtälöllä on yksi juuri. \(\require{color}\color{red}{\text{(+1p)}}\)
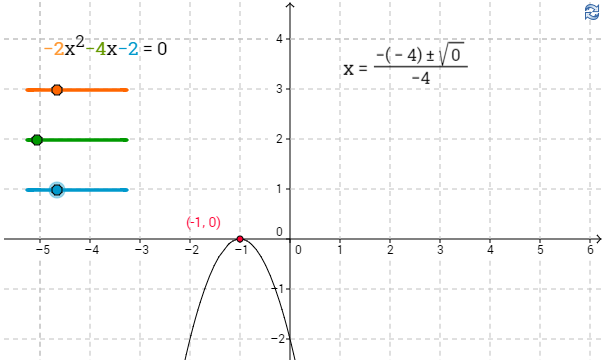
a) Tutki ja arvioi graafisesti, millä vakion $k$ arvoilla yhtälöllä $x^2+kx+1=0$ ei ole ratkaisua.
b) Ratkaise laskemalla, millä vakion $k$ arvoilla yhtälöllä $x^2+kx+1=0$ on kaksi ratkaisua.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a) Yhtälön $x^2+kx+1=0$ ratkaisuna ovat funktion $f(x)=x^2+kx+1$ nollakohdat. Funktion kuvaaja on ylöspäin aukeava paraabeli, jolla ei ole nollakohtia silloin, kun kuvaaja on kokonaan $x$-akselin yläpuolella. \(\require{color}\color{red}\text{(+1p)}\)
Funktion kuvaaja näyttäisi olevan $x$-akselin yläpuolella, kun $-2<k<2$.
Vastaus: $-2<k<2$. \(\require{color}\color{red}\text{(+1p)}\)
b) Toisen asteen yhtälöllä on kaksi ratkaisua, kun diskriminantti on positiivinen $(D>0)$.
\(\require{color}\begin{align*} D&=b^2-4ac && ||\ a=1, b=k, c=1\\ &=k^2-4 \cdot 1 \cdot1 \\ &=k^2-4 && \color{red}\text{(+1p)} \end{align*}\)
Ratkaistaan epäyhtälö $D>0$ eli $k^2-4>0$.
Kyseessä on toisen asteen lauseke, jonka kuvaaja on ylöspäin aukeava paraabeli. Lausekkeen arvo on positiivinen nollakohtien ulkopuolella.
\(\require{color}\begin{align*} k^2-4&=0\\ k^2&=4\\ k&=\pm2 && \color{red}\text{(+1p)} \end{align*}\)
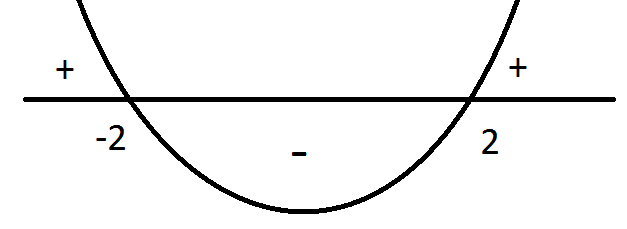\(\require{color}\color{red}\text{(Kuva +1p)}\)
Vastaus: $k<-2$ tai $k>2$. \(\require{color}\color{red}\text{(+1p)}\)
a) Jaa alla olevaa kuvaajaa hyödyntäen polynomi $-x^2+3x+4$ tekijöihinsä.
b) Jaa laskemalla polynomi $2x^2+2x+\frac12$ tekijöihinsä.
c) Ratkaise sekä graafisesti että laskemalla, millä vakion $b$ arvolla polynomilla $\frac12 x^2+bx-4$ on tekijä $x-4$.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
Toisen asteen polynomi saadaan jaettua tekijöihinsä nollakohtien avulla: $ax^2+bx+c=a(x-x_1)(x-x_2)$, missä $x_1$ ja $x_2$ ovat polynomin nollakohdat.
a)
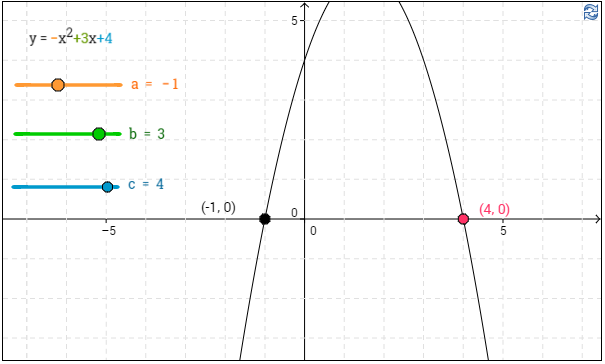
Kuvaajan perusteella havaitaan, että polynomin nollakohdat ovat $x_1=-1$ ja $x_2=4$. \(\require{color}\color{red}\text{(+1p)}\)
Vastaus: $-(x+1)(x-4)$. \(\require{color}\color{red}\text{(+1p)}\)
b) Jaetaan polynomi tekijöihinsä nollakohtien avulla.
\(\require{color}\begin{align*} x &=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\\\ &=\dfrac{-2 \pm \sqrt{2^2-4\cdot2\cdot \frac12}}{2\cdot 2}\\\\ x &=\dfrac{-2 \pm \sqrt{0}}{4}=\dfrac{-2}{4}=-\dfrac{1}{2} &&\color{red}\text{(+1p)} \end{align*}\)
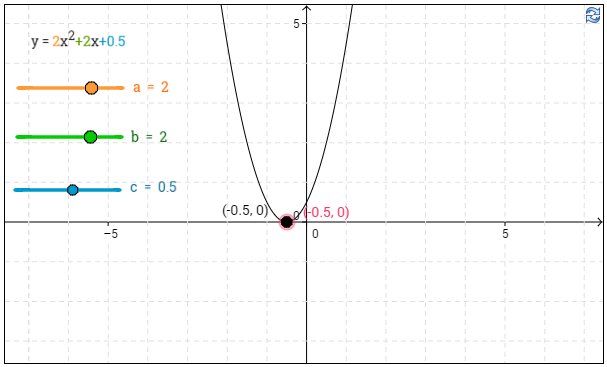
Kun toisen asteen polynomilla on vain yksi nollakohta, kutsutaan sitä kaksoisjuureksi.
Jaetaan tekijöihin: $2x^2+2x+\frac12=2(x-(-\frac12))(x-(-\frac12))=2(x+\frac12)^2$.
Vastaus: $2(x+\frac12)^2$. \(\require{color}\color{red}\text{(+1p)}\)
c) Toisen asteen polynomilla on tekijä $x-4$, jos ja vain jos $4$ on polynomin nollakohta.
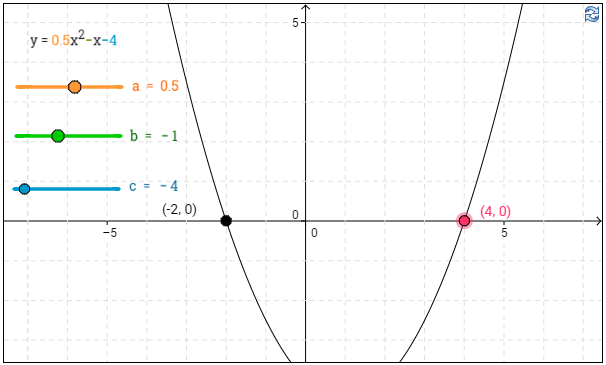
Kuvaajasta havaitaan, että tämä toteutuu polynomille $\frac12 x^2+bx-4$, kun $b=-1$. \(\require{color}\color{red}\text{(+1p)}\)
Laskemalla voidaan myös ratkaista, millä $b$:n arvolla $x=4$ on polynomin nollakohta.
\(\require{color}\begin{align*} \frac12 x^2+bx-4&=0 &&||x=4\\ \frac12\cdot4^2+b\cdot4-4&=0\\ 8+4b-4&=0\\ 4b+4&=0\\ 4b&=-4\\ b&=-1 &&\color{red}\text{(+1p)} \end{align*}\)
Vastaus: $b=-1$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: