Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.
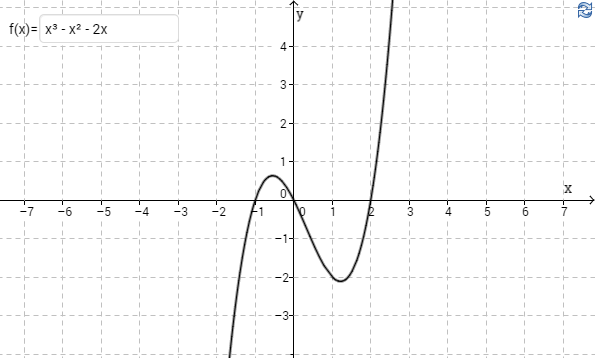
a) Ratkaise graafisesti yhtälö $x^3-x^2-2x=0$. (Kirjoita funktio syöttökenttään muodossa: x^3 – x^2 – 2x)
b) Ratkaise laskemalla yhtälö $x^3-x^2-2x=0$.
a) Kuvaajan perusteella yhtälön ratkaisut ovat $x\approx-1$ tai $x\approx0$ tai $x\approx2$. \(\require{color}\color{red}{\text{(+2p)}}\)
b) Ratkaistaan yhtälö jakamalla polynomi tekijöihin ja hyödyntämällä tulon nollasääntöä.
\(\require{color}\begin{align*}x^3-x^2-2x&=0 &&||\text{ yhteisenä tekijänä }x \\ x(x^2-x-2)&=0 &&\color{red}\text{(+1p)} \end{align*}\)
Tulon nollasääntö:
\(\require{color}\begin{align*}x=0 \text{ tai } x^2-x-2=0 &&\color{red}\text{(+1p)} \end{align*}\)
Ratkaistaan toisen asteen yhtälö ratkaisukaavalla:
\(\require{color}\begin{align*}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}&&||a=1, b=-1, c=-2\\\\x&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4\cdot1 \cdot (-2)}}{2\cdot1} &&\color{red}\text{(+1p)}\\\\ x&=\dfrac{1\pm\sqrt{9}}{2}=\dfrac{1\pm3}{2} \end{align*}\)
\(\require{color}\begin{align*}x=2 \text{ tai } x=-1 &&\color{red}\text{(+1p)} \end{align*}\)
Vastaus: $x=-1$ tai $x=0$ tai $x=2$.
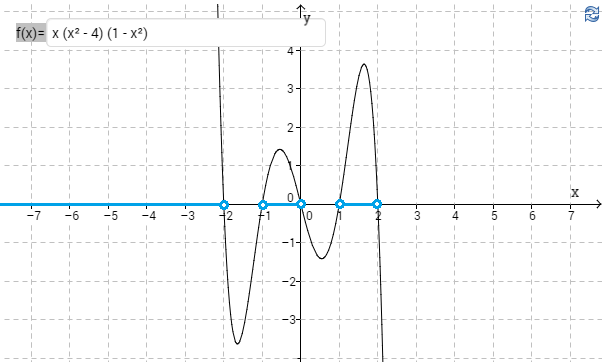
a) Ratkaise graafisesti epäyhtälö $x(x^2-4)(1-x^2)>0$. (Kirjoita funktio syöttökenttään muodossa: x(x^2 – 4)(1 – x^2)).
b) Ratkaise laskemalla epäyhtälö $x(x^2-4)(1-x^2)>0$.
(Jos GeoGebra ei lataudu, avaa se tästä linkistä. Koskee IE- ja Mozilla-selaimia.)
a) Kuvaajan perusteella epäyhtälön ratkaisut ovat $x<-2$ tai $-1<x<0$ tai $1<x<2$. \(\require{color}\color{red}{\text{(+2p)}}\)
b) Selvitetään merkkikaavion avulla, milloin tulo $x(x^2-4)(1-x^2)$ on positiivinen. Lasketaan ensin tulon tekijöiden nollakohdat ja hahmotellaan niiden kuvaajat.
Lausekkeen $x$ kuvaaja on nouseva suora ja nollakohta on $x=0$.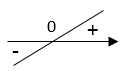 
\(\require{color}\color{red}{\text{(+1p)}}\)
Lausekkeen $x^2-4$ kuvaaja on ylöspäin aukeava paraabeli, jonka nollakohdat ovat:
\(\begin{align} x^2-4&=0\\ x^2&=4\\ x&=\pm2 \end{align}\)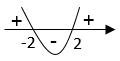 
\(\require{color}\color{red}{\text{(+1p)}}\)
Lausekkeen $1-x^2$ kuvaaja on alaspäin aukeava paraabeli, jonka nollakohdat ovat:
\(\begin{align} 1-x^2&=0\\ x^2&=1\\ x&=\pm1 \end{align}\)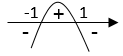 
\(\require{color}\color{red}{\text{(+1p)}}\)
Laaditaan merkkikaavio:
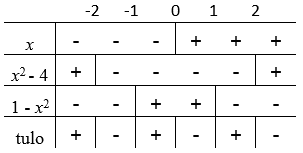
Vastaus: Merkkikaavion perusteella epäyhtälön ratkaisut ovat $x<-2$ tai $-1<x<0$ tai $1<x<2$. \(\require{color}\color{red}{\text{(+1p)}}\)
Ratkaise laskemalla epäyhtälö $-x^4-x^3+2x^2>0$.
(Voit hahmotella tilannetta alla olevan kuvaajan avulla syöttämällä syöttökenttään lausekkeen - x^4 - x^3 + 2x^2)
Jaetaan lauseke $-x^4-x^3+2x^2$ tekijöihin, joiden asteluku on enintään kaksi.
\(\begin{align} -x^4-x^3+2x^2=-x^2(x^2+x-2) \end{align}\) \(\require{color}\color{red}{\text{(+1p)}}\)
Selvitetään merkkikaavion avulla, milloin tulo $-x^2(x^2+x-2)$ on positiivinen. Lasketaan ensin tulon tekijöiden nollakohdat ja hahmotellaan niiden kuvaajat.
Lausekkeen $-x^2$ kuvaaja on alaspäin aukeava paraabeli ja nollakohta on $x=0$.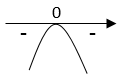 
\(\require{color}\color{red}{\text{(+1p)}}\)
Lausekkeen $x^2+x-2$ kuvaaja on ylöspäin aukeava paraabeli, jonka nollakohdat ratkaistaan ratkaisukaavalla:
\(\begin{align} x&=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-1\pm \sqrt{1^2-4\cdot1\cdot(-2)}}{2\cdot 1}\\ \\ &=\frac{-1\pm \sqrt{9}}{2}=\frac{-1\pm3}{2}\\ \\ x&=1 \text{ tai }x=-2 \end{align}\)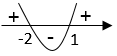 
\(\require{color}\color{red}{\text{(+1p)}}\)
Laaditaan merkkikaavio:
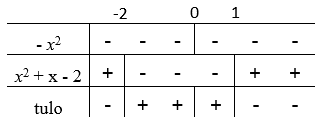\(\require{color}\color{red}{\text{(+2p)}}\)
Vastaus: Merkkikaavion perusteella epäyhtälön ratkaisut ovat $-2<x<0$ tai $0<x<1$. \(\require{color}\color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: