Päättele kuvaajan perusteella, milloin funktio f on vähenevä, kun kuvaaja esittää
a) funktiota f
b) funktion f derivaattaa f'
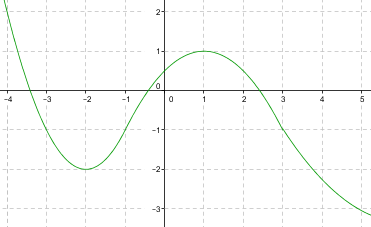
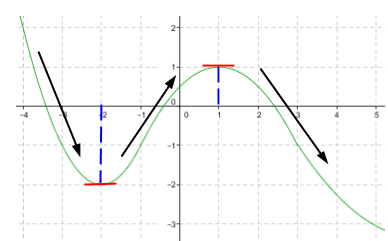
a) Funktion kulkusuunta muuttuu derivaatan nollakohdissa $x=-2$ ja $x=1$.
Merkitty kuvaan derivaatan nollakohdat kuvaan $\color{Red}{(+1\text{p})}$.
Merkitty kuvaan nuolet funktion kulkusuunnista $\color{Red}{(+1\text{p})}$.
Funktio on vähenevä väleillä $]-\infty, -2]$ ja $[2, \infty[. $
TAI
Funktio on vähenevä väleillä $x\leq -2$ ja $x \geq 2$ $\color{Red}{(+1\text{p})}$.
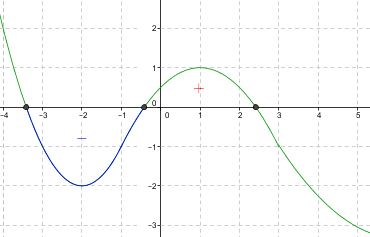
b) Funktion kulkusuunta muuttuu derivaatan nollakohdissa $x\approx -3,\! 41$, $x\approx -0,\! 41$ ja $x\approx 2,\! 41$.
Merkitty kuvaan derivaatan nollakohdat $\color{Red}{(+1\text{p})}$.
Merkitty, milloin derivaatan arvo on negatiivista ja milloin positiivista $\color{Red}{(+1\text{p})}$.
Funktio f on vähenevä välillä $[-3,\! 41; -0,\! 41]$ $\color{Red}{(+1\text{p})}$.
Tutki, milloin funktio $f(x)=x^3+x^2-5x+10$ on kasvava ja milloin vähenevä.
Derivoidaan funktio $f(x)=x^3+x^2-5x+10$:
$f'(x)=3x^2+2x-5$ $\color{Red}{(+1\text{p})}$
Ratkaistaan derivaatan nollakohdat $\color{Red}{(+1\text{p})}$:
\(\begin{align} x &= {-2 \pm \sqrt{2^2-4\cdot 3\cdot (-5)} \over 2\cdot 3} \\ &=\frac{-2 \pm \sqrt{4+60}}{6} \\ &=\frac{-2\pm 8}{6}\\ \end{align}\)
\(\begin{align} x&=\frac{-2+8}{6} & \text{ tai } \qquad x&= \frac{-2-8}{6} \\ &=\frac{6}{6} &&=\frac{-10}{6} \\ &=1 &&=-\frac{5}{3} \end{align}\)
Piirretään merkki- ja kulkukaavio:
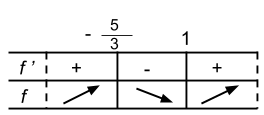
$f'(-2)=3\cdot (-2)^2+2\cdot (-2)-5=3>0$
$f'(0)=3+\cdot 0^2 + 2\cdot 0 - 5 = -5<0$
$f'(2)=3\cdot 2^2+2\cdot 2 -5 = 11>0$
Laskettu testipisteet $\color{Red}{(+1\text{p})}$
Merkki- ja kulkukaavio piirretty oikein $\color{Red}{(+1\text{p/rivi})}$
Vastaus: funktio on kasvava väleillä $]-\infty, -\frac{5}{3}]$ ja $[1, \infty [$ ja vähenevä välillä $[-\frac{5}{3}, 1]$ $\color{Red}{(+1\text{p})}$
Laske funktion $g(x)=2x^3-5x^2-4x+2$ suurin ja pienin arvo välillä $[-1,3]$.
Polynomifunktiolla on aina suurin ja pienin arvo suljetulla välillä. Suurin ja pienin arvo voivat sijaita joko välinpäätepisteissä tai derivaatan nollakohdissa. $\color{Red}{(+1\text{p})}$
Derivoidaan funktio $g(x)=2x^3-5x^2-4x+2$:
$g'(x)=6x^2-10x-4$ $\color{Red}{(+1\text{p})}$
Ratkaistaan derivaatan nollakohdat $\color{Red}{(+1\text{p})}$:
\(\begin{align} x &= {-(-10) \pm \sqrt{(-10)^2-4\cdot 6\cdot (-4)} \over 2\cdot 6} \\ &=\frac{10\pm \sqrt{100+96}}{12} \\ &=\frac{10 \pm 14}{12} \end{align}\)
\(\begin{align} x&=\frac{10+14}{12} & \text{ tai } \qquad x&=\frac{10-14}{12} \\ &=\frac{24}{12} & &=\frac{-4}{12} \\ &=2 &&=-\frac{1}{3} \end{align}\)
Lasketaan funktion arvo välin päätepisteillä ja derivaatan nollakohdilla $\color{Red}{(+\frac{1}{2}\text{p/laskettu arvo})}$:
$g(-1)=2\cdot (-1)^3-5\cdot (-1)^2-4\cdot (-1)+2=-1$
$g(-\frac{1}{3})=2\cdot (-\frac{1}{3})^3-5\cdot (-\frac{1}{3})^2-4\cdot (-\frac{1}{3})+2 =\frac{73}{27}\approx 2,\!70$
$g(2)=2\cdot 2^3-5\cdot 2^2-4\cdot 2+2=-10$
$g(3)=2\cdot 3^3-5\cdot 3^2-4\cdot 3+2=-1$
Vastaus: pienin arvo on $-10$ ja suurin arvo on $\frac{73}{27}$ $\color{Red}{(+1\text{p/arvo})}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
