Mekaanisen energian säilyminen ja työperiaate
Lapsi työntää lelutankkia 1,5 matkan, jolloin tankin nopeus muuttuu arvosta 0,0 m/s arvoon 0,30 m/s.
Kuinka suuri on tankkia liikuttava keskimääräinen kokonaisvoima, kun tankin massa on 300 g?

Kirjataan lähtöarvot
\(v_0=0,0 \text{ m/s}, \ v_1=0,30 \text{ m/s} \\ \Delta x=1,5 \text{ m}, \ m=0,300 \text{ kg}\)
Työperiaateen mukaan tankkiin kohdistuvan kokonaisvoiman tekemä työ
on yhtä suuri kuin tankin liike-energian muutos. \(\require{color}\color{red}{\text{(Työperiaate +1p)}}\)
\(W=\Delta E_k\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(F \cdot \Delta x = \dfrac{1}{2}mv_1^2-\dfrac{1}{2}mv_0^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(F \cdot \Delta x = \dfrac{1}{2}mv_1^2\)
\(F =\dfrac{\frac{1}{2}mv_1^2}{\Delta x}\)
\(F =\dfrac{mv_1^2}{2\Delta x}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(F =\dfrac{0,300\text{ kg} \cdot (0,30 \text{ m/s})^2}{2\cdot 1,5 \text{ m}}\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(F = 0,0090 \text{ N}\)
Vastaus: Voiman suuruus on noin 9,0 mN.\(\require{color}\color{red}{\text{(+1p)}}\)
Pulkkaa työnnetään peilikirkkaalla jäällä suoraan eteenpäin.
Oheinen kuvaaja kuvaa pulkkaa työntävän voiman suuruutta sen paikan funktiona.
Mikä on pulkan loppunopeus, kun pulkka lähtee levosta? Pulkan massa on 15 kg.
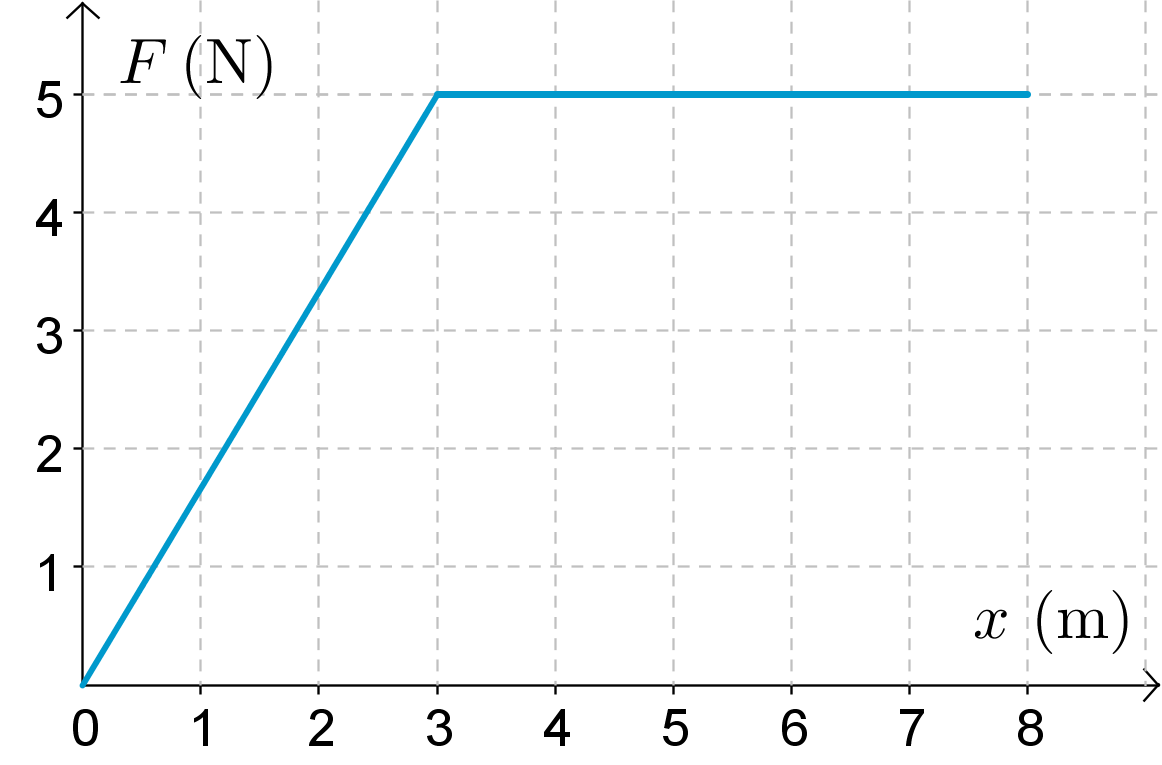
(x, F) -koordinaatiston kuvaajan alle jäävä pinta-ala kuvaa voiman tekemää työtä.
Oletetaan, että pulkkaan kohdistuvat vastusvoimat ovat pieniä, jolloin työntävän voiman
tekemä työ kuluu kokonaisuudessaan pulkan liike-energian muutokseen. \(\require{color}\color{red}{\text{(+1p)}}\)
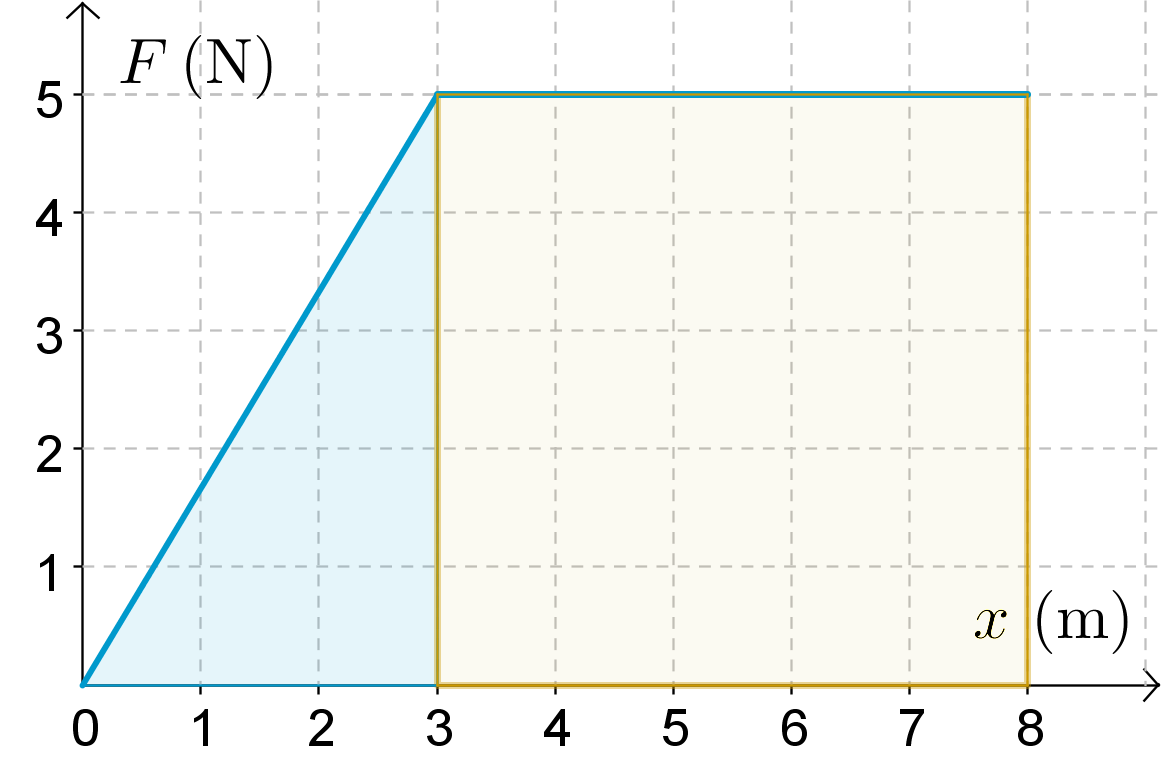
Kuvaajan alle jäävän pinta-alan suuruus
\(\dfrac{1}{2}\cdot 3 \cdot 5 + 5 \cdot 5 = 32,5 \)
Yhtä ruutua vastaava työ
\(W_1 = F \Delta x = 1,0 \text{ N} \cdot 1,0 \text{ m}=1,0 \text{ J}\)
Työntävän voiman tekemä kokonaistyö
\(W = 32,5 \text{ J}\)\(\require{color}\color{red}{\text{(+1p)}}\)
Työperiaatteen mukaan kapaleeseen vaikuttavan kokonaisvoiman
tekemä työ on yhtä suuri kuin kappaleen liike-energian muutos eli \(\require{color}\color{red}{\text{(+1p)}}\)
\(W=\Delta E_k \)
\(F \Delta x = \dfrac{1}{2}mv_1^2-\dfrac{1}{2}mv_0^2\)
\(W=\dfrac{1}{2}mv_1^2-\dfrac{1}{2}mv_0^2\)
\(W=\dfrac{1}{2}mv_1^2\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(2W=mv_1^2\)
\(v_1=\sqrt{\dfrac{2W}{m}}\)
\(v_1=\sqrt{\dfrac{2 \cdot 32,5 \text{ J}}{15 \text{ kg}}}\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(v_1 \approx 2,08 \text{ m/s}\)
Vastaus: Pulkan loppunopeus on noin 2,1 m/s. \(\require{color}\color{red}{\text{(+1p)}}\)
Auto saapuu mäen alaosaan nopeudella 60 km/h, jonka jälkeen kuljettaja nostaa jalan kaasulta.
Kuinka korkean mäen yli auto korkeintaan pääsee, kun autoon kohdistuvat vastusvoimat ovat merkityksettömät?

Kirjataan lähtöarvot \(v_0=60 \text{ km/h}\)
Oletetaan, että auton mekaaninen energia säilyy ja
että autoon kohdistuvat vastusvoimat ovat merkityksettömät.\(\require{color}\color{red}{\text{(+2p)}}\)
\(E_{p1}+E_{k1}=E_{p0}+E_{k0}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(mgh_1+\dfrac{1}{2}mv_1^2=mgh_0+\dfrac{1}{2}mv_0^2\)
\(mgh_1=\dfrac{1}{2}mv_0^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(gh_1=\dfrac{1}{2}v_0^2\)
\(h_1=\dfrac{v_0^2}{2g}\)
\(h_0=\dfrac{\big(\frac{60}{3,6}\text{m/s}\big)^2}{9,81 \text{ m/s}^2}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(h_1 \approx 28,3 \text{ m}\)
Vastaus: Korkeintaan 28 metriä korkean mäen yli. \(\require{color}\color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
