Millä vakion $k$ arvoilla yhtälöllä $3x^2 - k^4x = - k^6$ ei ole reaalisia ratkaisuja?
Muokataan yhtälö muotoon $3x^2 - k^4x + k^6 = 0$
Reaalisia ratkaisuja ei ole, kun diskriminantti $D = b^2 - 4ac < 0$ \(\require{color}\color{red}\text{(+1p)}\)
\(\begin{align} (-k^4)^2-4 \cdot3\cdot k^6 &<0\\ k^8-12k^6&<0 \end{align}\) \(\require{color}\color{red}\text{(+1p)}\)
Ratkaistaan nollakohdat: $k^8 - 12k^6 = 0$
Otetaan $k^6$ yhteiseksi tekijäksi: $k^6(k^2 - 12) = 0$
Tulon nollasäännön nojalla:
\(\begin{align*} k^6 &= 0 &\text{tai } & & k^2 - 12 &= 0\\ k &= 0 &\text{tai }& & k^2 &= 12\\ & & & & k &= \pm \sqrt{12}\\ & & & & k &= \pm 2 \sqrt{3} \qquad \require{color}\color{red}\text{(+1p)} \end{align*}\)
Merkkiperustelut:
$k^6 \geq 0$ kaikilla k:n arvoilla, koska eksponentti on parillinen.
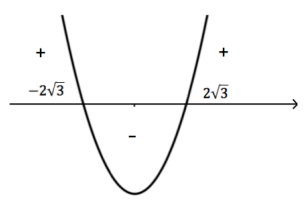\(\require{color}\color{red}\text{(+1p)}\)
Tehdään merkkikaavio:
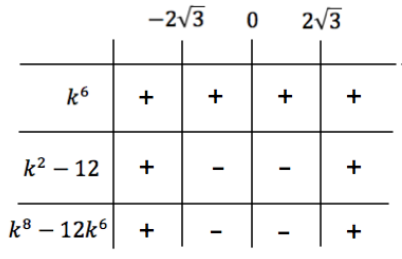\(\require{color}\color{red}\text{(+1p)}\)
Vastaus: Reaalisia ratkaisuja ei ole, kun $-2\sqrt{3}< k < 2 \sqrt{3}$. \(\require{color}\color{red}\text{(+1p)}\)
(Toinen merkintätapa: \(x\in{]-2\sqrt{3},\; 2\sqrt{3}\ [}\))
Osaisitko tarkastella vastauksen oikeellisuutta GeoGebran ja/tai oman laskimen grafiikkatoimintojen avulla?
a) Määritä vakion $a$ arvo siten, että polynomilla $2x^3 - 4x^2 + x - a$ on yhtenä tekijänä binomi $x-2$.
b) Mikä on tällöin epäyhtälön $2x^3 - 4x^2 + x - a < 0$ ratkaisu?
a) Huomataan ryhmittelemällä ja/tai kokeilemalla, että $a$:n arvoksi pitää valita 2, jotta saadaan $x-2$ yhteiseksi tekijäksi.
\(\begin{align} &2x^3 - 4x^2 + x - a\\ =& 2x^2(x - 2) +1\cdot( x - a) &&||a=2\\ =& 2x^2(x - 2) +1\cdot( x - 2)\\ =&(2x^2+1)(x - 2) && \require{color}\color{red}{\text{(+3p)}} \end{align}\)
b) Käytetään epäyhtälön ratkaisussa tulomuotoa:
$(2x^2+1)(x - 2)<0$
Ratkaistaan nollakohdat:
\(\begin{align*} 2x^2+1&=0 & &\text{tai }& x-2&=0\\ 2x^2&=-1 & &\text{tai }& x&=2\\ x^2&=-\frac{1}{2} & &\text{tai }& x&=2 \qquad \color{red}{\text{(+1p)}}\\ \text{ei } &\text{ratkaisua} \end{align*}\\ \)
Merkkitarkastelut:
- $2x^2+1$ on ylöspäin aukeava paraabeli, jolla ei ole nollakohtia. Siis $2x^2+1>0$ kaikilla $x$:n arvoilla.
- $x-2$ on nouseva suora, joten nollakohdan vasemmalla puolella arvot ovat negatiivisia ja oikealla puolella positiivisia.
- Siis $x-2$ määrää merkin. \(\require{color}\color{red}\text{(+1p)}\)
$2x^3 - 4x^2 + x - 2 < 0$, kun $x-2<0$ eli $x<2$.
Vastaus: $a=2$ ja epäyhtölön ratkaisu on $x<2$. \(\require{color}\color{red}\text{(+1p)}\)
a) Määritä ympyrän ja neliön pinta-alojen suhde, kun niiden piirit ovat samat (tarkka arvo).
b) Laske kolmen merkitsevän numeron tarkkuudella, kuinka monta prosenttia ympyrän ala on suurempi kuin neliön ala.
(Voit tarkistaan ympyrän ja neliön kaavat taulukkokirjasta.)
Kootaan tarvittavat kaavat:
- Ympyrän piiri $=2\pi r$
- Neliön piiri $=4a$
- Ympyrän ala $=\pi r^2$
- Neliön ala $=a^2$
a) Merkitään piirit yhtäsuuriksi: $2\pi r=4a$. \(\require{color}\color{red}\text{(+1p)}\)
Ratkaistaan tästä $a=\dfrac{\pi r}{2}$. \(\require{color}\color{red}\text{(+1p)}\)
Sijoitetaan saatu $a$:n lauseke neliön alan kaavaan, merkitään pinta-alojen suhde ja sievennetään.
\(\require{color} \begin{align*} &\frac{\pi r^2}{(\frac{\pi r}{2})^2} && \color{red}{\text{(+1p)}}\\\\ =&\frac{\pi r^2}{\frac{\pi^2r^2}{4}} =\frac{4\pi r^2}{\pi^2 r^2}\\\\ =&\underline{\underline{\frac{4}{\pi}}}&& \color{red}{\text{(+1p)}} \end{align*} \)
b) $\dfrac{4}{\pi}\approx 1,27323...$
\(\begin{align} 1,27323...-1&=0,27323... \quad \require{color}\color{red}\text{(+1p)}\\ &\approx0,273\\ &=27,3\% \end{align}\)
Vastaus: Ympyrän ala on 27,3 % suurempi kuin neliön ala. \(\require{color}\color{red}\text{(+1p)}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: