Suorakulmaisen kolmion ominaisuuksista.
Onko kolmio suorakulmainen?
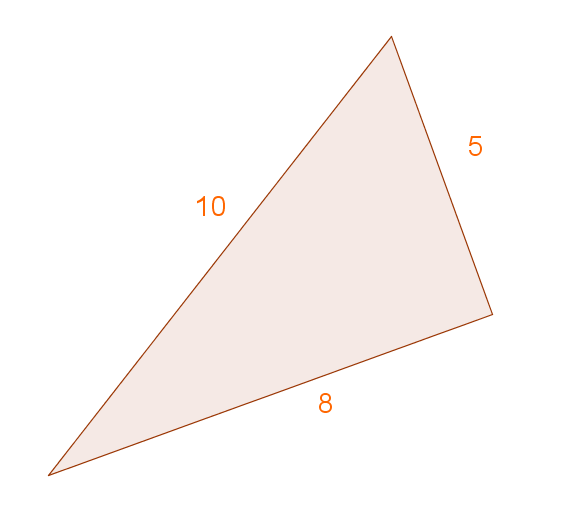
Jos kolmio on suorakulmainen, niin kolmion sivujen
pituudet toteuttavat pythagoraan lauseen
\(a^2+b^2=c^2\) \(\color{Red}{\text{(+2p)}}\)
Hypotenuusa on pisin sivu eli \(c=10\)
Kateetit ovat lyhimpiä sivuja eli\(\ a=8, \ b=5\)
Tarkistetaan toteutuuko pythagoraan lause
\(\quad a^2+b^2\)
\(=8^2+5^2\)
\(=64+25\)
\(=89\) \(\color{Red}{\text{(+1p)}}\)
\(\quad c^2\)
\(=10^2\)
\(=100\) \(\color{Red}{\text{(+1p)}}\)
Koska \(89 \neq 100\), niin pythagoraan lause
ei toteudu ja kolmio ei ole suorakulmainen. \(\color{Red}{\text{(+2p)}}\)
Vastaus: Kolmio ei ole suorakulmainen.
Ratkaise kolmio

Merkitään kuvaan tuntemattoman sivut ja tuntematon kulma.
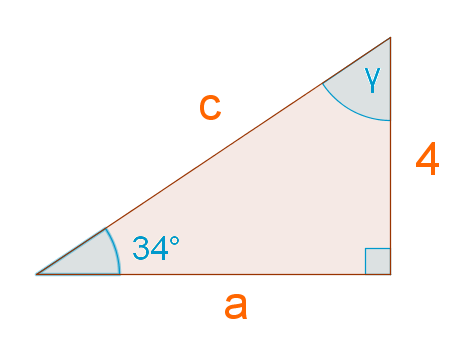
Koska kolmion kulmien summa on 180 astetta, niin
\(34^{\circ}+90^{\circ}+\beta=180^{\circ}\)
\(124^{\circ}+\beta=180^{\circ}\)
\(\beta = 180^{\circ}-124^{\circ}\)
\(\beta = 56^{\circ}\) \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan tangentin avulla kateetin a pituus.
\(\tan 34^{\circ}=\dfrac{4}{a} \qquad\qquad ||\cdot a\) \(\color{Red}{\text{(+1p)}}\)
\(a \cdot \tan 34^{\circ} = 4 \quad \qquad ||:\tan 34^{\circ}\)
\(a=\dfrac{4}{\tan 34^{\circ}}\)
\(a\approx 5,93\) \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan sinin avulla hypotenuusan c pituus
\(\sin 34^{\circ}=\dfrac{4}{c} \qquad\qquad ||\cdot a\) \(\color{Red}{\text{(+1p)}}\)
\(c \cdot \sin 34^{\circ} = 4 \quad \qquad ||:\sin 34^{\circ}\)
\(c=\dfrac{4}{\sin 34^{\circ}}\)
\(c \approx 7,2\) \(\color{Red}{\text{(+1p)}}\)
Vastaus: Kolmion kulmat ovat 34, 56 ja 90 astetta. Sivujen pituudet ovat 4, 5.93 ja 7.2. \(\color{Red}{\text{(+1p)}}\)
Ratkaise kolmio
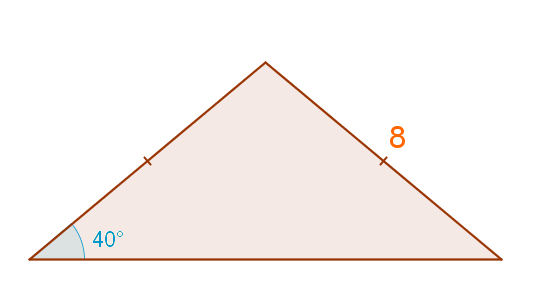
Kolmio on tasakylkinen.
Tasakylkisella kolmiolla on seuraavat ominaisuudet
- kolmiolla on kaksi yhtä pitkää sivua (kylkeä)
- kantakulmat ovat yhtä suuret
- kannalle piirretty korkeusjana puolittaa kolmion huippukulman.
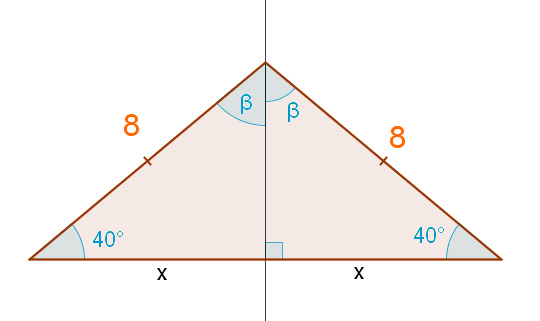
\(\color{Red}{\text{(+1p kuvasta)}}\)
Ratkaistaan sivun x pituus kosinin avulla.
\(\cos 40^{\circ}=\dfrac{x}{8} \qquad \qquad ||\cdot 8\) \(\color{Red}{\text{(+1p)}}\)
\(8 \cos 40^{\circ} = x\)
\(x \approx 6,13\) \(\color{Red}{\text{(+1p)}}\)
Kolmion kanta on siis
\(2 x \approx 12,3\) \(\color{Red}{\text{(+1p)}}\)
Koska kolmion kulmien summa on 180 astetta, niin
\(2\beta + 40^{\circ}+40^{\circ}=180^{\circ}\)
\(2 \beta = 100^{\circ}\) \(\color{Red}{\text{(+1p)}}\)
Vastaus: Kolmion sivujen pituudet ovat 12.3, 8 ja 8.
Kolmion kulmien suuruudet ovat 40, 40 ja 100 astetta. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
