Suureet, graafinen malli, merkitsevät numerot, matemaattinen malli
a) Millainen tiede fysiikka on?
b) Anna kolme esimerkkiä fysiikan tutkimuskohteista.

a) Fysiikka on
- kokeellinen luonnontiede \(\quad \color{red}{\text{(+1,5p)}}\)
- eksakti luonnontiede \(\quad \color{red}{\text{(+1,5p)}}\)
Fysiikka pyrkii löytämään lainalaisuuksia, joita
voidaan mallintaa matemaattisesti
koetella kokeellisesti
b) Fysiikka tutkii esimerkiksi
- liikettä
- ainetta
- energiaa
- perusluonteisia luonnonlakeja
- perusvuorovaikutuksia
- kaikkeutta
- makromaailmaa (aistein havaittava todellisuus)
- mikromaailmaa (apuvälinein havaittava todellisuus)
\(\quad \color{red}{\text{(+1p / esimerkki)}}\)
a) Mitä tarkoittaa suure? Mitä eroa on
skalaari- ja vektorisuureella?
b) Minkä kahden perussuureen johdannaissuure on nopeus?
c) (i) Muunna kymmenpotenssimuotoon 900 nm
(ii) Muunna kymmenpotenssimuotoon 52 GJ

a) Suure on jonkin asian tai esineen mitattava ominaisuus \(\quad \color{red}{\text{(+1p)}}\)
Skalaarisuureella on vain suuruus (esim. massa) \(\quad \color{red}{\text{(+0,5p)}}\)
Vektorisuureella on suuruus ja suunta (esim. nopeus)\(\quad \color{red}{\text{(+0,5p)}}\)
b) Nopeus määritellään siirtymän ja kuluneen ajan suhteena.
\(\text{nopeus}= \dfrac{\text{paikan muutos}}{\text{kulunut aika}}\) \(\quad \color{red}{\text{(+1p)}}\)
\(v=\dfrac{\Delta x}{\Delta t}\)
Perussuureet ovat siis matka ja aika.\(\quad \color{red}{\text{(+1p)}}\)
c)
(i)
\(\quad 900 \text{ nm}\)
\(= 900 \cdot 10^{-9} \text{ m} \)
\(= 9 \cdot 10^{-7} \text{ m}\)\(\quad \color{red}{\text{(+1p)}}\)
(ii)
\(\quad 52 \text{ GJ} \)
\(=52 \cdot 10^{9} \text{J}\)
\( \\ =5,2 \cdot 10^{10}\text{ J}\)\(\quad \color{red}{\text{(+1p)}}\)
Erään aineen massan ja tilavuuden välistä riippuvuutta tutkittaessa
saatiin seuraavanlaiset mittaustulokset
\(\begin{array}{|c|c|} \hline \text{massa (g)} & \text{tilavuus (ml)} \\ \hline 11,8 & 15,0 \\ 23,7 & 30,0 \\ 39,5 & 50,0 \\ 47,3 & 60,0 \\ 71,0 & 90,0 \\ \hline \end{array}\)
a) Määritä sopivaa graafista esitystä käyttäen aineen tiheys. (5p)
b) Mikä aine on kyseessä? (1p)
Sijoitetaan mittaustulokset (V, m) -koordinaatistoon.
Synonyymeja:
- Piirretään massa m tilavuuden V funktiona.
- Sijoitetaan mittaustulokset Vm -koordinaatistoon.
Huom! \(1 \text{ ml} = 1 \text{ cm}^3\)
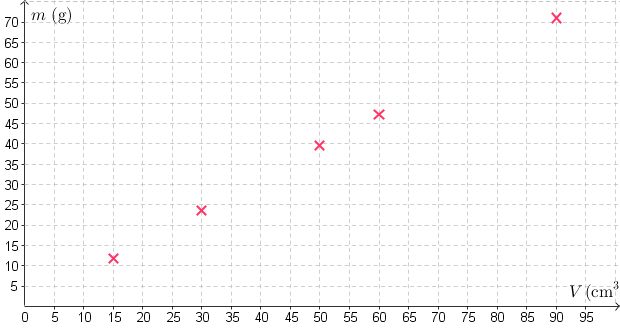
Huom! Muista kirjoittaa suureiden
tunnukset ja yksiköt akseleihin!
\(\quad \color{red}{\text{(Akselit oikeinpäin, nimetty ja yksiköt +2p)}}\)
Suureiden välinen riippuvus on lineaarista, joten
sovitetaan suora mittauspisteiden kautta.
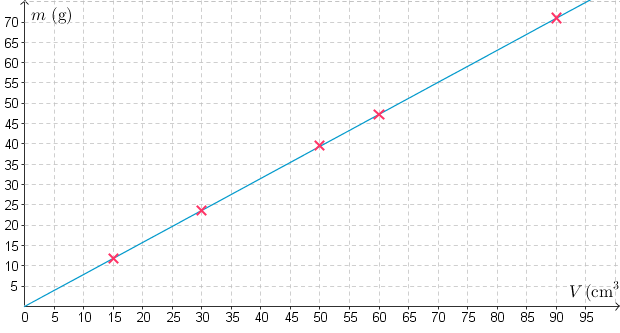
\(\quad \color{red}{\text{(Sovitettu suora +1p)}}\)
Ratkaistaan suoran fysikaalinen kulmakerroin, joka on
aineen tiheys.
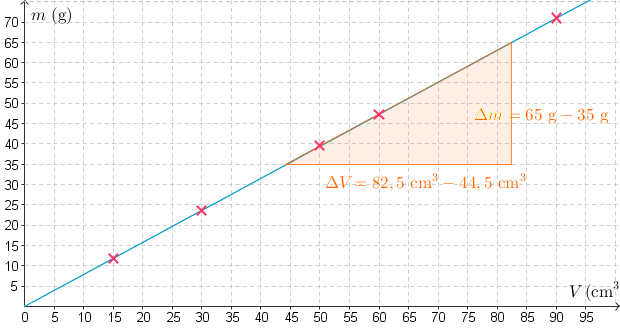
Aineen tiheydeksi saadaan
\(\rho=\dfrac{\Delta m}{\Delta V} \) \(\quad \color{red}{\text{(+1p)}}\)
\(\rho=\dfrac{65 \text{ g} - 35 \text{ g}}{82,5 \text{ cm}^3 - 44,5 \text{ cm}^3} \)
\(\rho \approx 0,79 \text{ g/cm}^3\)
\(\quad \color{red}{ 0,786 \text{ g/cm}^3\leq\rho \leq 0,794 \text{ g/cm}^3\text{(+1p)}}\)
b) Taulukkokirjasta huomataan, että aineen tiheys on lähimpänä
etanolin tiheyttä ( \(0,789 \text{ g/cm}^3\)) eli aine on mitä todennäköisimmin etanolia. \(\quad \color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
