Ratkaise tehtävät alla olevan GeoGebran avulla. Piirrä kuviot myös omaan vihkoosi.
Muodosta kaksi keskenään erimuotoista
a) nelikulmiota, joiden pinta-ala on 4,
b) suunnikasta, joiden pinta-ala on 12,
c) puolisuunnikasta, joiden pinta-ala on 10,
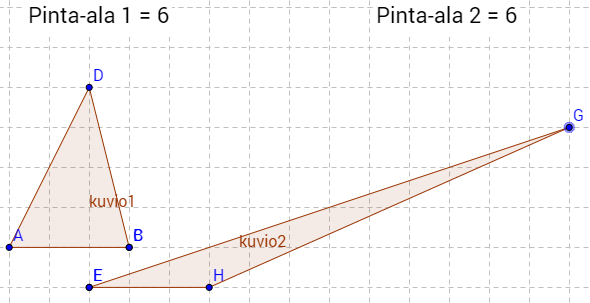
d) tasakylkistä kolmiota, joiden pinta-ala on 6,
e) suorakulmaista kolmiota, joiden pinta-ala on 6,
f) tylppäkulmaista kolmiota, joiden pinta-ala on 6.
a) Nelikulmio on monikulmio, jossa on neljä kulmaa ja sivua. Piirretty kaksi erilaista nelikulmiota: \(\require{color}\color{red}\text{(+1p)}\)
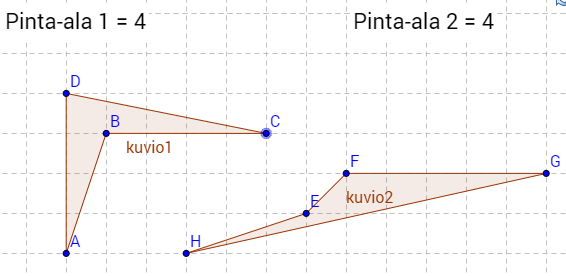
b) Suunnikas on nelikulmio, jonka vastakkaiset sivut ovat yhdensuuntaiset. Piirretty kaksi erilaista suunnikasta: \(\require{color}\color{red}\text{(+1p)}\)
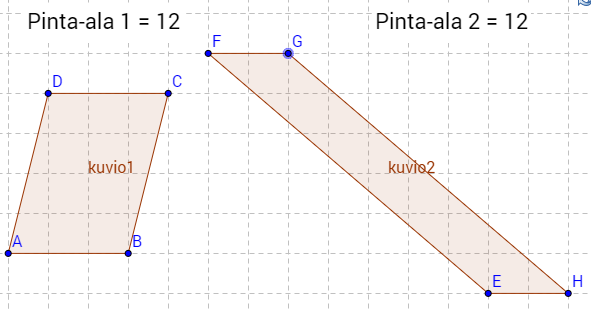
c) Puolisuunnikas on nelikulmio, jonka kaksi vastakkaista sivua ovat yhdensuuntaisia. Piirretty kaksi erilaista puolisuunnikasta: \(\require{color}\color{red}\text{(+1p)}\)
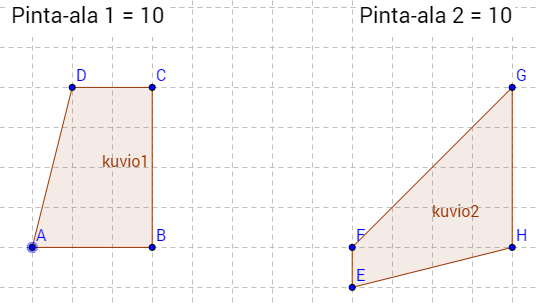
d) Tasakylkinen kolmio on kolmio, jossa kaksi sivua ovat keskenään yhtä pitkät. Piirretty kaksi erilaista tasakylkistä kolmiota: \(\require{color}\color{red}\text{(+1p)}\)
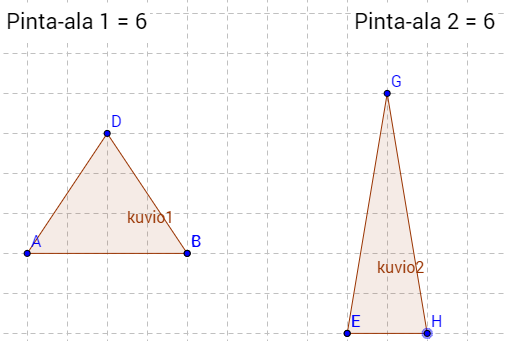
e) Suorakulmainen kolmio on kolmio, jossa yksi kulma on suora eli 90 astetta. Piirretty kaksi erilaista suorakulmaista kolmiota: \(\require{color}\color{red}\text{(+1p)}\)
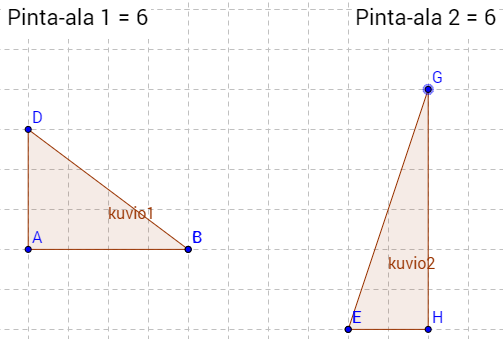
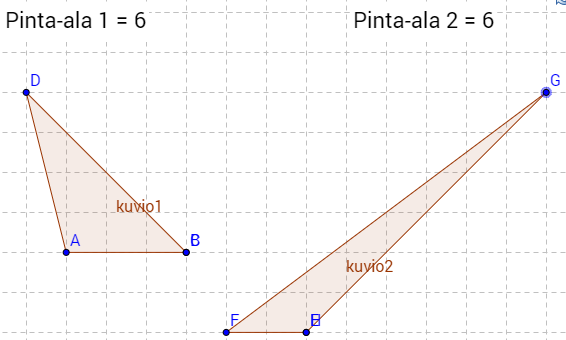
f) Tylppäkulmainen kolmio on kolmio, jossa yksi kulmista on yli 90 astetta. Piirretty kaksi erilaista tylppäkulmaista kolmiota: \(\require{color}\color{red}\text{(+1p)}\)
Laske alla olevat tehtävät. Tarkista laskusi piirtämällä kuviot GeoGebralla.
a) Mikä on neliön sivun pituus ja pinta-ala, jos sen piiri on 12 ruutua?
b) Mikä on suunnikkaan pinta-ala, jos sen yhden sivun pituus on 5 ruutua ja korkeus 3 ruutua. Kuinka monta tällaista keskenään erilaista suunnikasta pystyt piirtämään?
c) Mikä on kolmion pinta-ala, jos sen kanta on 3 ruutua ja korkeus 4 ruutua. Kuinka monta tällaista keskenään erilaista kolmiota pystyt piirtämään?
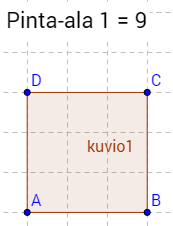
a) Jos neliön piiri on 12 ruutua, on sen sivun pituus $\tfrac{12}{4} = 3$ ruutua. \(\require{color}\color{red}\text{(+1p)}\)
Tällöin neliön pinta-ala on $3^2=9$ ruutua. \(\require{color}\color{red}\text{(+1p)}\)
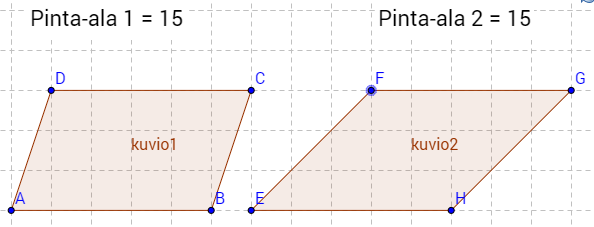
b) Suunnikkaan pinta-ala on sen kannan ja korkeuden tulo. $5 \cdot 3 = 15$. \(\require{color}\color{red}\text{(+1p)}\)
Tällaisia suunnikkaita on olemassa äärettömän monta erilaista. Piirretty vähintään kaksi erilaista: \(\require{color}\color{red}\text{(+1p)}\).
c) Kolmion pinta-ala on puolet kannan ja korkeuden tulosta. $\dfrac{3 \cdot 4}{2}=6$. \(\require{color}\color{red}\text{(+1p)}\)
Tällaisia kolmioita on olemassa äärettömän monta erilaista. Piirretty vähintään kaksi erilaista: \(\require{color}\color{red}\text{(+1p)}\).
Laske
a) suorakulmion pinta-ala, kun leveys on 3,0 cm ja korkeus on 6,2 cm.
b) suorakulmaisen kolmion pinta-ala, kun kannan pituus on 2,4 m ja korkeus 5,0 m.
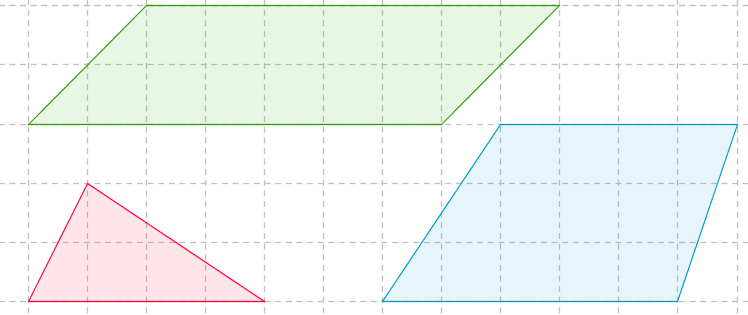
c) alla olevan kuvan monikulmioiden pinta-alat.
a) \(A=3,0 \cdot 6,2 = 18,6\) $\color{Red}{(+1\text{p})}$
Vastaus: \(19 \text{ cm}^2\quad\color{Red}{(+\frac{1}{2}\text{p})}\)
b) \(A=\dfrac{2,4\cdot 5,0}{2}=\dfrac{12,0}{2}=6,0\) $\color{Red}{(+1\text{p})}$
Vastaus: \(6,0 \text { m}^2 \quad\color{Red}{(+\frac{1}{2}\text{p})}\)
c) Suunnikkaan pinta-ala: \(A=2\cdot 7=14\) $\color{Red}{(+1\text{p})}$
Kolmion pinta-ala: \(A= \dfrac{2\cdot 4}{2}=4\) $\color{Red}{(+1\text{p})}$
Puolisuunnikkaan pinta-ala: \(A=\dfrac{(4+5)\cdot 3}{2} = \dfrac{27}{2}=13,5\) $\color{Red}{(+1\text{p})}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
