keskinopeus, nopeus ja kiihtyvyys
Auton keskinopeus on 85 km/h.
a) Kuinka monta metriä auto etenee yhdessä sekunnissa?
b) Kuinka kauan autolta kuluu 50 km matkaan?

Ratkaisu a-kohtaan.
Kirjataan lähtöarvot \(v_k = 85 \text{ km/h}\)
Muutetaan nopeuden yksiköksi m/s.
\(v_k=85 \text{ km/h} \)
\(v_k= \dfrac{85}{3,6} \text{ m/s}\) \(\quad \color{red}{\text{(+1p)}}\)
\(v_k \approx 24 \text{ m/s}\) \(\quad \color{red}{\text{(+1p)}}\)
Vastaus: Auto etenee 24 metriä yhdessä sekunnissa. \(\quad \color{red}{\text{(+1p)}}\)
\(\Big(85 \text{ km/h}=85 \frac{1000 \text{ m}}{3600 \text{ s}}=\dfrac{85}{3,6} \text{ m/s} \Big)\)
Ratkaisu b-kohtaan.
Kirjataan lähtöarvot \(s=50 \text{ km}, \ v_k=85 \text{ km/h}\)
Keskinopeus \(v_k\) on \(v_k = \dfrac{s}{t}\).
Ratkaistaan suureyhtälöstä aika \(t\).
\(v_k = \dfrac{s}{t} \qquad || \cdot t\)
\(v_k \cdot t = s \ \ \quad ||:t\)
\(t=\dfrac{s}{v_k}\) \(\quad \color{red}{\text{(+1p)}}\)
Sijoitetaan lukuarvot.
\(t=\dfrac{50 \text{ km}}{85 \text{ km/h}}\) \(\quad \color{red}{\text{(+1p)}}\)
\(t \approx 0,588 \text{ h}\)
\(t \approx 35 \text{ min}\)
Vastaus: noin 35 minuuttia. \(\quad \color{red}{\text{(+1p)}}\)
Alla olevassa aika-paikka-koordinaatistossa on esitetty avaruudessa
etenevän raketin liike aikavälillä 0,0 ... 10 s.
a) Millaista raketin liike on?
b) Mikä on raketin nopeus?
c) Piirrä raketin nopeuden kuvaaja aika-nopeus-koordinaatistoon.
Ratkaisu a-kohtaan
Raketin liike on tasaista, koska \(\quad \color{red}{\text{(+1p)}}\)
- raketti etenee samassa ajassa aina yhtä pitkän matkan.
- raketin paikan kuvaaja on suora.
\(\quad \color{red}{\text{(Kumpi tahansa perustelu +1p)}}\)
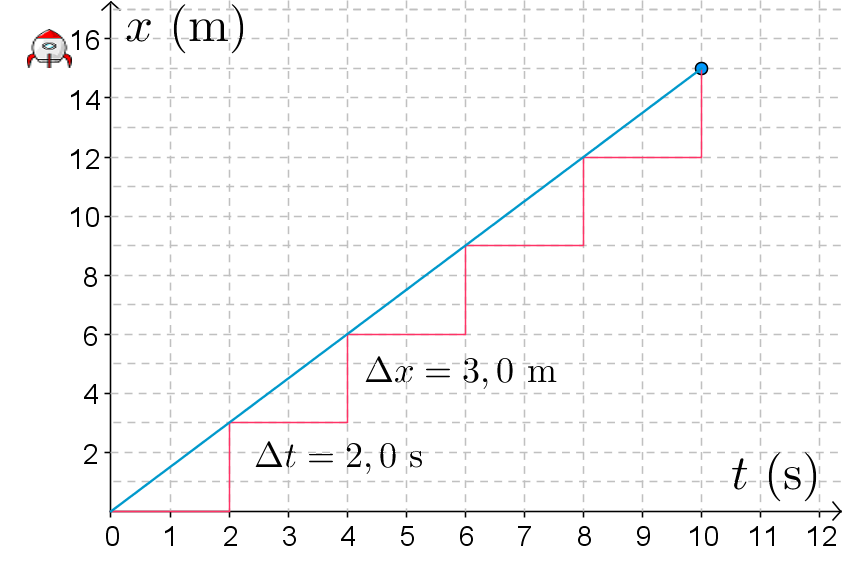
Ratkaisu b-kohtaan
- Paikan kuvaajan fysikaalinen kulmakerroin on kappaleen nopeus.
- (t, x) -koordinaatistoon piirretyn kuvaajan kulmakerroin on kappaleen nopeus.
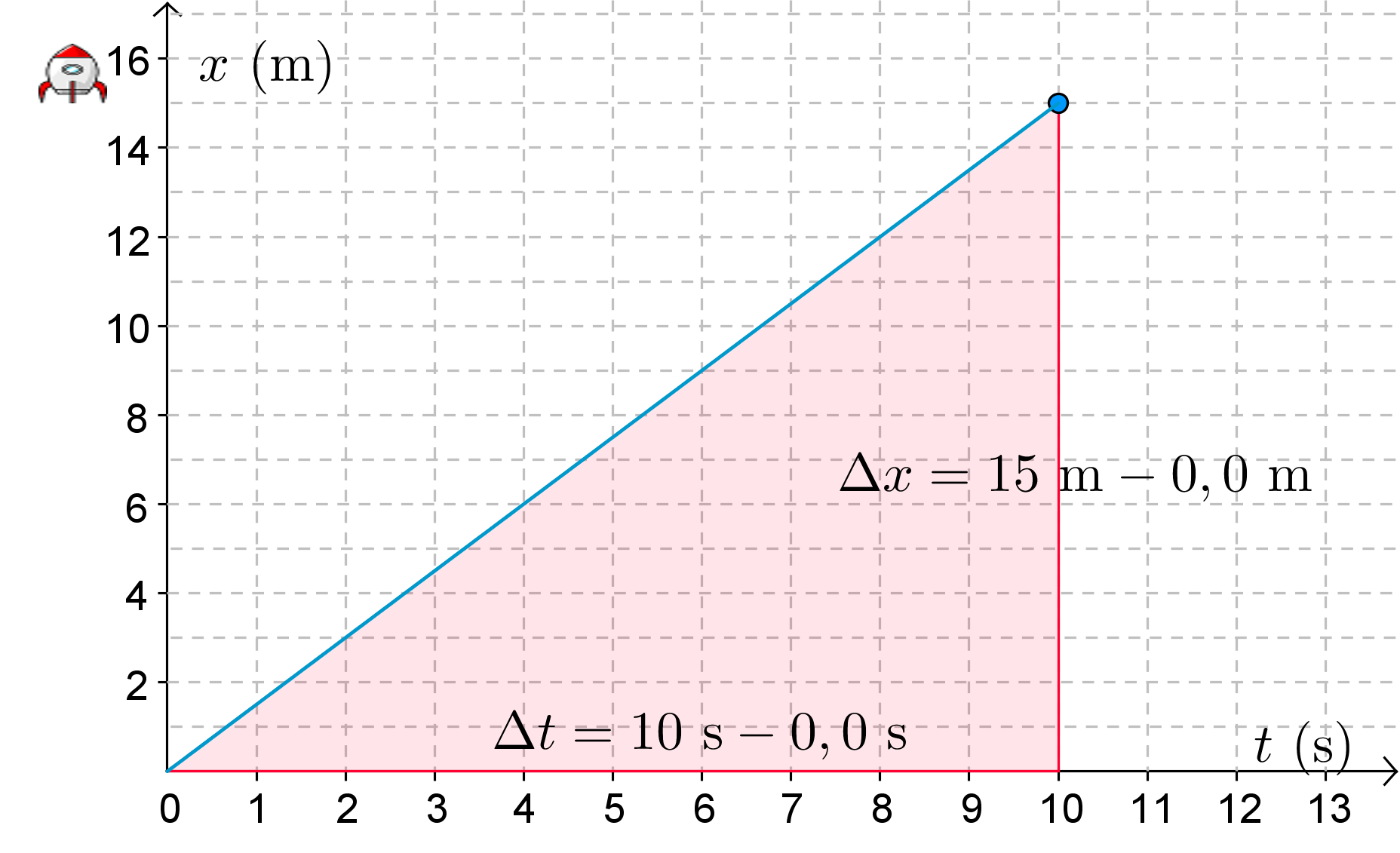
\(\quad \color{red}{\text{(Kulmakertoimen hakeminen +1p)}}\)
\(v=\dfrac{\Delta x}{\Delta t}\)
\(v=\dfrac{15 \text{ m}}{10 \text{ s}}\)
\(v=1,5 \text{ m/s}\) \(\quad \color{red}{\text{(+1p)}}\)
Ratkaisu c-kohtaan
- Nopeuden kuvaaja on vaakasuora, koska raketin liike on tasaista.
Nopeus on 1,5 m/s, joten piirretään vaakasuora viiva ajanhetkestä 0,0 s ajanhetkeen 10 s korkeudelle 1,5 m/s.
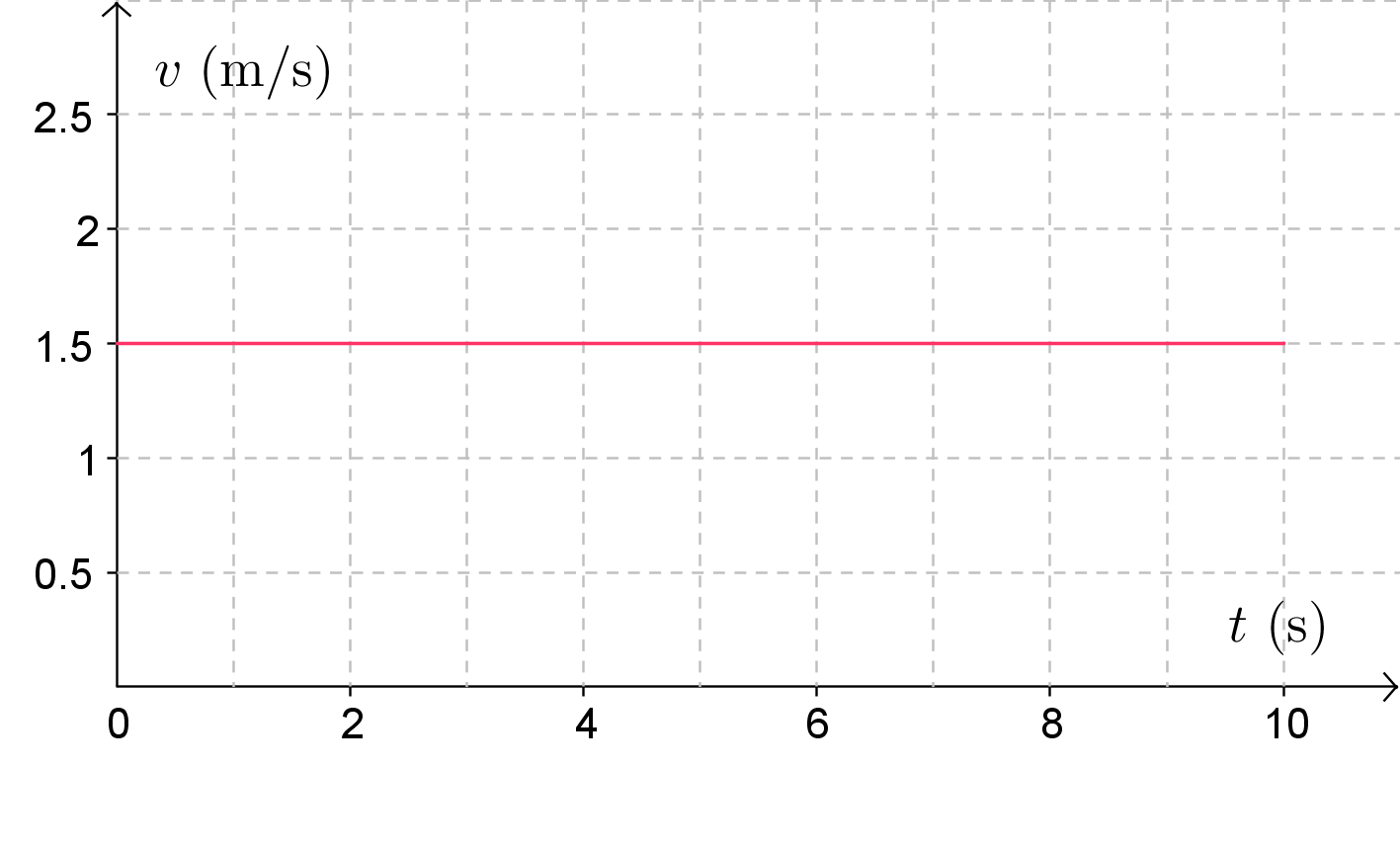
\(\quad \color{red}{\text{(Kuvaaja oikein +2p)}}\)
Pappatunturin kiihtyvyys on \(0,60 \text{ m/s}^2\).
Kuinka kauan kestää, että pappatunturin nopeus muuttuu
arvosta 30 km/h arvoon 45 km/h?

Ratkaisu
Kirjataan lähtöarvot
\(v_0 = 30 \text{ km/h}, \ v=45 \text{ km/h}, \ a = 0,60 \text{ m/s}^2\)
Oletetaan, että pappatunturin nopeus muuttuu tasaisesti.
Ratkaistaan kulunut aika kiihdytyksen suureyhtälöstä.
\(a = \dfrac{\Delta v}{\Delta t}\ \qquad || \cdot \Delta t\) \(\quad \color{red}{\text{(+1p)}}\)
\(a \Delta t = \Delta v \ \ \quad ||:a\)
\(\Delta t = \dfrac{\Delta v}{a}\) \(\quad \color{red}{\text{(+2p)}}\)
\(\Delta t = \dfrac{v-v_0}{a}\)
Sijoitetaan lukuarvot.
Huom! Nopeus pitää muuttaa perusyksikköön!
\(\Delta t= \dfrac{\frac{45}{3,6}\text{ m/s} - \frac{30}{3,6} \text{ m/s}}{0,60 \text{ m/s}^2}\) \(\quad \color{red}{\text{(+2p)}}\)
\(\Delta t \approx 6,9 \text{ s}\)
Vastaus: Kiihdytykseen kuluu noin 6,9 sekuntia. \(\quad \color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
